Старая квантовая теория

При уменьшении температуры максимум спектральной интенсивности излучения абсолютно чёрного тела сдвигается к более длинным длинам волны, а его высота уменьшается. Кривые спектральной интенсивности (слева) сравниваются с классической формулой Рэлея — Джинса (справа).

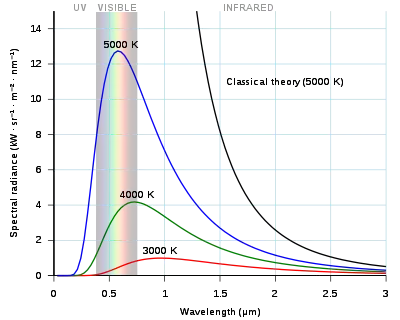
Одна из главных задач физики конца XIX века — проблема излучения абсолютно чёрного тела. Абсолютно чёрное тело — это физическая идеализация: тело, которое полностью поглощает падающее излучение любых длин волн. Реальные же вещества чёрного цвета, например, сажа, поглощают 99 % падающего излучения в видимом диапазоне длин волн, однако инфракрасное излучение поглощается ими значительно хуже. Среди тел Солнечной системы абсолютно чёрному телу лучше всего соответствует Солнце.

Согласно классической термодинамике спектральная интенсивность I(ν) излучения должна быть одинаковой для любых абсолютно чёрных тел, нагретых до одинаковой температуры. Такое предсказание подтверждается экспериментом. Спектральная интенсивность достигает максимума при некоторой частоте ν_max, а по обе стороны от максимума падает до нуля. Частота максимума ν_max, как и его высота, увеличивается с температурой.

Попытки теоретически предсказать форму экспериментальной кривой спектральной интенсивности абсолютно чёрного тела на основе законов классической физики привели к формуле Рэлея — Джинса[6][7]:

${\displaystyle I(\nu )={\frac {2\pi }{c^{2}}}kT\nu ^{2}.}$

Кроме области малых частот, закон формулы Рэлея — Джинса не согласуется с экспериментом. Он предсказывает, что полная интенсивность излучаемой энергии бесконечно растёт с частотой (ультрафиолетовая катастрофа), но в действительности полная интенсивность конечна.

В 1900 году Макс Планк постулировал[4], что обмен энергией между атомами и испущенным ими электромагнитным излучением происходит дискретными порциями энергии, а наименьшая порция энергии при заданной частоте ν равна

${\displaystyle E=h\nu }$,

где h — постоянная Планка. При этом при взаимодействии атомов и излучения могут передаваться только целые кратные порции энергии hν. Используя этот постулат, Планк вывел формулу для спектральной интенсивности теплового равновесного электромагнитного излучения абсолютно чёрного тела:

${\displaystyle I(\nu )={\frac {2\pi \nu ^{2}}{c^{2}}}{\frac {h\nu }{e^{\frac {h\nu }{kT}}-1}},}$

что прекрасно согласуется с экспериментом. Таким образом, Планк решил проблему излучения абсолютно чёрного тела, используя противоречащую классической физике идею о квантовании энергии.

Фотоэффект — явление эмиссии веществом электронов под действием света (и, вообще говоря, любого электромагнитного излучения). Первые систематические исследования фотоэффекта выполнены русским физиком Столетовым в 1888 году, который установил несколько важных закономерностей. Ключевым моментом оказался тот факт, что энергия фотоэлектронов абсолютно не зависит от интенсивности падающего света: повышение интенсивности увеличивает лишь число выбиваемых электронов, но не их скорость. Однако оказалось, что скорость электронов зависит от частоты излучения, причём с увеличением частоты энергия фотоэлектронов растёт линейно. Такие явления были непонятны с позиции классической электродинамики.

Теоретическое объяснение фотоэффекта дал Альберт Эйнштейн в 1905 году. Используя гипотезу Планка, он предположил, что свет не только излучается порциями (квантами), но и вообще представляет собой поток квантов (фотонов) с энергией hν. При фотоэффекте часть падающего света отражается от поверхности, а другая часть проникает внутрь поверхностного слоя металла и поглощается там. Когда электрон поглощает фотон, он получает от него энергию и, затрачивая часть её на работу выхода A_out, покидает металл. Таким образом, имеем уравнение Эйнштейна для фотоэффекта:

${\displaystyle h\nu =A_{out}+P+eV,}$

где P — энергия ионизации (которую для металлов можно положить нулю, поскольку металл имеет большое количество свободных электронов), eV — кинетическая энергия фотоэлектрона. Это уравнение было вскоре интенсивно проверено в экспериментах Роберта Милликена, за которые в том числе он получил Нобелевскую премию по физике 1923 года.

Таким образом, явление фотоэффекта является экспериментальным подтверждением гипотезы Планка и наличия у света корпускулярных свойств.

Эксперимент по неупругому рассеянию электронов на атомах, поставленный в 1913—1914 годах Джеймсом Франком и Густавом Людвигом Герцом[8], подтвердил справедливость постулатов Бора.

В этом опыте атомы или молекулы более-менее разреженного газа бомбардируются медленными электронами. При этом исследуется распределение скоростей электронов до и после столкновений. Если столкновения упругие, то распределение скоростей не меняется; и наоборот, при неупругих столкновениях часть электронов теряет свою энергию, отдавая её атомам, с которыми они сталкивались, поэтому распределение скоростей меняется.

В результате опыта Франка — Герца обнаружилось, что:

• при скоростях электронов, которые меньше некоторой критической скорости, столкновение является полностью упругим, то есть электрон не передаёт атому свою энергию, но отскакивает от него, меняя только направление своей скорости;
• при достижении критической скорости удар становится неупругим, то есть электрон теряет часть своей энергию и передаёт её атому, который при этом переходит в другое стационарное состояние, характеризующееся большей энергией.

Гармонический осциллятор — простейшая система старой квантовой теории. Запишем гамильтониан:

${\displaystyle {\mathcal {H}}={\frac {p^{2}}{2m}}+{\frac {m\omega ^{2}q^{2}}{2}}.}$

Энергетические уровни системы определяются орбитами движения, а орбиты отбираются согласно следующему квантовому правилу: площадь в фазовом пространстве, которую покрывает каждая орбита, должна быть целой. Отсюда следует, что энергия квантуется по правилу Планка:

${\displaystyle E_{n}=n\hbar \omega ,}$

известный результат, по которому формулируется правило квантования старой квантовой теории. Следует отметить, что этот результат отличается от настоящего на ${\displaystyle \hbar \omega /2}$, поскольку из квантовой механики известно, что нулевой уровень для гармонического осциллятора имеет энергию ${\displaystyle \hbar \omega /2}$.

Термодинамические величины для квантованного гармонического осциллятора можно определить с помощью усреднения энергии в каждом из дискретных состояний:

${\displaystyle U={\frac {1}{Z}}\sum \limits _{n}n\hbar \omega e^{-{\frac {n\hbar \omega }{kT}}}={\hbar \omega e^{-{\frac {\hbar \omega }{kT}}} \over 1-e^{-{\frac {\hbar \omega }{kT}}}},}$

где ${\displaystyle k}$ — постоянная Больцмана, ${\displaystyle T}$ — абсолютная температура (которая измеряется в более естественных энергетических единицах), ${\displaystyle Z=\sum \limits _{n}e^{-{\frac {n\hbar \omega }{kT}}}}$ — статистическая сумма. Легко видеть, что при очень низких температурах (то есть когда величина ${\displaystyle \beta ={\frac {1}{kT}}}$ является большой) средняя энергия гармонического осциллятора ${\displaystyle U}$ очень быстро — экспоненциально — достигает нуля. Причина состоит в том, что ${\displaystyle kT}$ является характерной энергией произвольного движения при температуре ${\displaystyle T}$, и если она меньше ${\displaystyle \hbar \omega }$, её не хватает для того, чтобы передать осциллятору хотя бы один квант энергии. Поэтому гармонический осциллятор остаётся в основном состоянии.

Это означает, что при очень низких температурах изменение энергии относительно ${\displaystyle \beta }$ (и, естественно, температуры) является малым. Изменение энергии относительно температуры — это теплоёмкость; поэтому теплоёмкость является малой при низких температурах, стремясь к нулю как

${\displaystyle e^{-{\frac {\hbar \omega }{kT}}}.}$

При высоких температурах (то есть при малых ${\displaystyle \beta }$) средняя энергия ${\displaystyle U}$ равна ${\displaystyle kT}$. Этот факт согласуется с законом равнораспределения классической термодинамики: каждый гармонический осциллятор при температуре ${\displaystyle T}$ имеет среднюю энергию ${\displaystyle kT}$. Это означает, что теплоёмкость осциллятора постоянна (в классической механике) и равна постоянной Больцмана ${\displaystyle k}$. Для совокупности атомов, которые соединены пружинами (приемлемая модель твердого тела), полная теплоёмкость равна ${\displaystyle Nk}$, где ${\displaystyle N}$ — количество осцилляторов. В целом каждому атому сопоставляют три осциллятора, учитывая три возможных направления колебаний в трёх измерениях. Поэтому теплоёмкость классического твёрдого тела при достаточно высокой температуре равна ${\displaystyle 3k}$ на атом, или ${\displaystyle 3R}$ на моль, — закон Дюлонга — Пти.

Одноатомные твёрдые тела при комнатных температурах имеют приблизительно такую же теплоёмкость — ${\displaystyle 3k}$ на атом, но при низких температурах это не так. С уменьшением температуры теплоёмкость также уменьшается и достигает нуля при абсолютном нуле температур. Это факт подтверждается для всех материальных систем и составляет третий закон термодинамики. Классическая механика не может объяснить третий закон термодинамики, поскольку в её рамках считается, что теплоёмкость не зависит от температуры.

Это противоречие между классической механикой и теплоёмкостью холодных тел заметил в XIX веке Максвелл; устранение этого противоречия было сложной задачей для тех, кто отстаивал атомарную теорию материи. Альберт Эйнштейн решил эту проблему в 1906 году, предложив идею квантования атомарного движения и сформулировав модель Эйнштейна — первое применение квантовой теории к механическим системам. Немного позже Петер Дебай развил более точную количественную теорию теплоёмкости твёрдых тел на основе квантованных гармонических осцилляторов с разными частотами (модель Дебая).

При любой энергии E можно легко найти импульс p при помощи закона сохранения энергии:

${\displaystyle p={\sqrt {2m(E-V(q))}}.}$

Это выражение интегрируется по всем значениям q между классическими точками поворота, где импульс равен нулю.

Простейший случай — частица в прямоугольной потенциальной яме длиной L, для которой условие квантования выглядит следующим образом:

${\displaystyle 2\int _{0}^{L}pdq=nh,}$

откуда импульс:

${\displaystyle p={\frac {nh}{2L}}.}$

Интегрируя правую часть уравнения для импульса, можно найти энергетические уровни:

${\displaystyle E_{n}={\frac {n^{2}h^{2}}{8mL^{2}}}.}$

Рассмотрим другой потенциал — линейный, который соответствует постоянной силе F. Квантовомеханическая формулировка этой задачи довольно сложна, и, в отличие от рассмотренных выше случаев, полуклассический результат не является точным, а лишь стремится к таковому при увеличении значений квантовых чисел. Имеем:

${\displaystyle 2\int _{0}^{\frac {E}{F}}{\sqrt {2m(E-Fx)}}dx=nh,}$

что даёт условие квантования:

${\displaystyle {4 \over 3}{\sqrt {2m}}{E^{3/2} \over F}=nh,}$

откуда можно определить энергетические уровни:

${\displaystyle E_{n}=\left({\frac {3F}{4{\sqrt {2m}}}}nh\right)^{2/3}.}$

Полуклассический результат этой задачи совпадает с квантовомеханическим в случае вычисления энергии основного состояния. Условие квантования будет иметь вид:

${\displaystyle 2\int _{-{\sqrt {\frac {2E}{k}}}}^{\sqrt {\frac {2E}{k}}}{\sqrt {2m\left(E-{\frac {1}{2}}kx^{2}\right)}}\ dx=nh,}$

откуда определяем энергетические уровни:

${\displaystyle E=n{\frac {h}{2\pi }}{\sqrt {\frac {k}{m}}}=n\hbar \omega ,}$

где ${\displaystyle \omega }$ — угловая частота.

Ротатор состоит из тела массы M, которое закреплено на безмассовом жёстком стержне длиной R, и описывается следующим двумерным лагранжианом:

${\displaystyle {\mathcal {L}}_{2D}={\frac {MR^{2}{\dot {\varphi }}^{2}}{2}},}$

из которого можно выразить угловой момент ${\displaystyle L}$, зависящий от полярного угла ${\displaystyle \varphi }$:

${\displaystyle L=MR^{2}{\dot {\varphi }}.}$

Старая квантовая теория требует, чтобы угловой момент был квантованным:

${\displaystyle L=n\hbar .}$

В модели Бора такого условия квантования, которое накладывается на круговые орбиты, достаточно для определения энергетического спектра.

Трёхмерный жёсткий ротатор описывается двумя углами θ и φ сферической системы координат относительно произвольно выбранной оси Oz. Опять в лагранжиан входит только кинетическая энергия:

${\displaystyle {\mathcal {L}}_{3D}={\frac {MR^{2}{\dot {\theta }}^{2}}{2}}+{\frac {MR^{2}({\dot {\varphi }}\sin \theta )^{2}}{2}},}$

Канонические импульсы будут иметь вид:

${\displaystyle p_{\theta }={\dot {\theta }},}$

${\displaystyle p_{\varphi }={\dot {\varphi }}\sin ^{2}\theta .}$

Уравнение для φ тривиальное, ${\displaystyle p_{\varphi }}$ является константой:

${\displaystyle p_{\varphi }=l_{\varphi },}$

что равно z-компоненте углового момента. Далее из условия квантования следует, что после интегрирования по углу φ от 0 до 2π:

${\displaystyle l_{\varphi }=m\hbar ,}$

где m — так называемое магнитное квантовое число. Название происходит из-за того, что z-компонента углового момента равна магнитному моменту ротатора вдоль оси Oz (очевидно, если частица, находящаяся на конце ротатора, заряжена).

Полный угловой момент трёхмерного ротатора квантован аналогично двумерному. Два условия квантования определяют произвольные значения полного углового момента и его z-компоненты с помощью квантовых чисел l, m. Эти условия присутствуют и в квантовой механике, но во времена господства старой квантовой теории было непонятно, как может быть квантованной ориентация углового момента относительно произвольно выбранной оси Oz. Казалось, что отсюда должно было бы следовать существование некоторого выделенного направления в пространстве.

Это явление получило название пространственного квантования, но оно казалось несовместимым с изотропностью пространства. В квантовой механике угловой момент квантуется таким же образом, но его дискретные состояния вдоль одной оси являются суперпозицией состояний вдоль других осей, поэтому в процессе квантования не возникает какого-либо выделенного направления в пространстве. Поэтому сейчас термин «пространственное квантование» не употребляется, а вместо него используют термин «квантование углового момента».

Угловая часть атома водорода — это ротатор, который характеризуется квантовыми числами l, m. Остаётся неизвестной только радиальная координата, которая задаётся одномерным периодическим движением.

При фиксированном значении полного углового момента L функция Гамильтона классической задачи Кеплера имеет вид (здесь переменные выбраны таким образом, чтобы масса и энергия стали безразмерными):

${\displaystyle {\mathcal {H}}={\frac {p^{2}}{2}}+{\frac {l^{2}}{2r^{2}}}-{\frac {1}{r}}.}$

Фиксируя энергию как (отрицательную) константу и решая полученное уравнение относительно импульса p, имеем условие квантования:

${\displaystyle 2\int {\sqrt {2E-{\frac {l^{2}}{r^{2}}}+{\frac {2}{r}}}}\ dr=kh,}$

что определяет новое квантовое число k, которое в совокупности с числом l определяет энергетические уровни:

${\displaystyle E_{k,l}=-{\frac {1}{2(k+l)^{2}}}.}$

Легко видеть, что энергия зависит от суммы квантовых чисел k и l, которую можно обозначить как ещё одно квантовое число n, которое называется главным квантовым числом. Если k неотрицательное, то разрешённые значения числа l при заданном n не могут быть больше заданного значения n.

Эта полуклассическая модель атома водорода имеет название модели Зоммерфельда, а орбитами электрона в ней являются эллипсы. Модель Зоммерфельда предсказывала тот факт, что магнитный момент атома, который измеряется вдоль некоторой оси, будет иметь только дискретные значения. Этот результат, казалось, противоречил изотропности пространства, но был подтверждён опытом Штерна — Герлаха. Теория Бора — Зоммерфельда являлась одним из самых важных этапов развития квантовой механики, поскольку описывала возможность расщепления энергетических уровней атома в магнитном поле, то есть объясняла эффект Зеемана.

Релятивистское решение для энергетических уровней атома был найден Арнольдом Зоммерфельдом[2]. Запишем релятивистское уравнение для энергии с электростатическим потенциалом:

${\displaystyle E=m_{0}c^{2}\left({\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}-1\right)-k{\frac {Ze^{2}}{r}}}$

и сделаем замену ${\displaystyle u={\frac {1}{r}}}$:

${\displaystyle {\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=1+{\frac {E}{m_{0}c^{2}}}+k{\frac {Ze^{2}}{m_{0}c^{2}}}u.}$

Выпишем выражения для импульсов:

${\displaystyle p_{r}=m{\dot {r}},}$

${\displaystyle p_{\varphi }=mr^{2}{\dot {\varphi }},}$

тогда их соотношение будет равно ${\displaystyle {\frac {p_{r}}{p_{\varphi }}}=-{\frac {du}{d\varphi }}}$, и отсюда можно получить уравнение движения (уравнение Бине):

${\displaystyle {\frac {d^{2}u}{d\varphi ^{2}}}=-\left(1-k^{2}{\frac {Z^{2}e^{4}}{c^{2}p_{\varphi }^{2}}}\right)u+{\frac {m_{0}kZe^{2}}{p_{\varphi }^{2}}}\left(1+{\frac {E}{m_{0}c^{2}}}\right)=-\omega _{0}^{2}u+K,}$

решение которого имеет вид:

${\displaystyle u={\frac {1}{r}}=K+A\cos \omega _{0}\varphi .}$

Угловое смещение перицентра за один период составляет

${\displaystyle \Delta \varphi =2\pi \left({\frac {1}{\omega _{0}}}-1\right).}$

Условия квантования в нашем случае будут выглядеть следующим образом:

${\displaystyle \oint p_{\varphi }d\varphi =2\pi p_{\varphi }=n_{\varphi }h,}$

${\displaystyle \oint p_{r}dr=p_{\varphi }\oint \left({\frac {1}{r}}{\frac {dr}{d\varphi }}\right)^{2}d\varphi =n_{r}h,}$

откуда можно вычислить энергетические уровни:

${\displaystyle {\frac {E_{n_{r},n_{\varphi }}}{m_{0}c^{2}}}=\left(1+{\frac {\alpha ^{2}Z^{2}}{(n_{r}+{\sqrt {n_{\varphi }^{2}-\alpha ^{2}Z^{2}}})^{2}}}\right)^{-1/2}-1,}$

где ${\displaystyle \alpha ={\frac {2\pi ke^{2}}{hc}}}$ — постоянная тонкой структуры. Этот результат совпадает с решением уравнения Дирака[9]. Кроме того, если сделать замены квантовых чисел ${\displaystyle n_{r}\to n_{r}+1/2}$ и ${\displaystyle n_{\varphi }\to l+1/2}$, то полученная формула будет совпадать с точным решением уравнения Клейна — Гордона[10].