Спор Ньютона и Лейбница о приоритете

Дифференциальный треугольник Паскаля

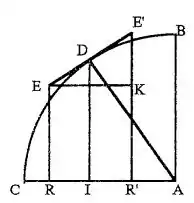
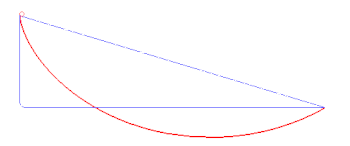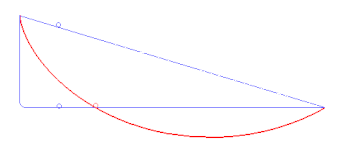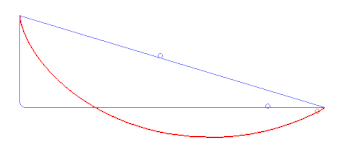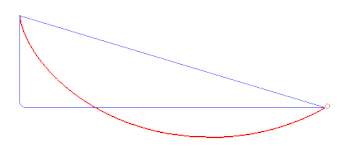
Ко времени Ньютона и Лейбница европейские математики уже внесли значительный вклад в формирование идей математического анализа. Развитием античного «метода исчерпаний» для вычисления площадей и объёмов занимались голландец Симон Стевин (1548—1620), итальянец Лука Валерио (1553—1618), немец Иоганн Кеплер (1571—1630). Идеи последнего, видимо, повлияли — напрямую или через посредство Галилео Галилея — на разработанный Бонавентурой Кавальери (1598—1647) «метод неделимых»[6]. Галилей также занимался разработкой вопроса о понятии бесконечно большой и бесконечно малой величин[7]. В 1639 году Кавальери получил важнейший результат, проинтегрировав степенную функцию. В период между 1636 и 1655 годами практически независимо друг от друга это достижение повторили во Франции Жиль Роберваль (1602—1675), Блез Паскаль (1623—1662), Пьер Ферма (1601—1665) и в Англии Джон Валлис (1616—1703)[8]. В 1626 году Грегуар де Сен-Венсан, развивая «метод исчерпаний», пришёл к идее представления кривой как предела, вписанного в многоугольник или описанного вокруг многоугольника, однако, поскольку он позиционировал своё достижение как решение задачи квадратуры круга, оно было проигнорировано большинством современных ему математиков; впоследствии его репутация была восстановлена Ньютоном и Лейбницем[9]. В своей работе «Трактат о синусах четверти круга» («Traité des sinus du quart de cercle», 1659) Паскаль вплотную приблизился к установлению связи между задачей построения касательной к кривой и вычислением площади под ней. В этой работе приводится изображение фигуры, впоследствии ставшей известной как «дифференциальный треугольник» и иллюстрирующей предельный переход при стремлении приращений аргумента и функции к нулю. Однако Паскаль, как и в 1624 году Виллеброрд Снелл (1580—1626), не сделал этого перехода. В опубликованной в 1638 году работе Пьер Ферма предложил метод определения максимумов и минимумов, сводящийся, в современной терминологии, к определению нулей первой производной. Решая задачу поиска центра тяжести параболического сегмента, Ферма пришёл к выводу о связи задач поиска касательной и вычисления площади[10]. Несмотря на то, что свои методы Ферма применял только к рациональным функциям, он ближе всех приблизился к изобретению математического анализа — за исключением, возможно, Исаака Барроу (1630—1677)[11]. Важное значение имела публикация в 1668 году книги «Logarithmotechnia» Николаса Меркатора (1620—1687), в которой было приведено разложение в степенной ряд натурального логарифма («ряд Меркатора») и указано его применение для вычисления площади под гиперболой[12].

Барроу — учитель Ньютона[комм. 2] — в своих математических построениях сильно тяготел к их геометрической интерпретации. Его метод вычисления касательных основывался на результатах континентальных математиков, а также англичан Джеймса Грегори (1638—1675) и Джона Валлиса. Вероятно, ему также были известны работы Ферма по анализу, изданные посмертно в 1679 году[14]. Основной труд Барроу в области анализа «Lectiones Geometricae» был издан в 1670 году. В 1673 году его приобрёл Лейбниц, но, по его утверждению, не читал[15].

Историки математики по-разному оценивают роль Ньютона и Лейбница в контексте достижений их предшественников. Согласно Эдмунду Хоппе (1928), можно выделить две независимые линии в истории математического анализа — кинематическую, которая ведёт к Ньютону через Платона, Архимеда, Галилея, Кавальери и Барроу, и атомистическую, к Лейбницу через Демокрита, Кеплера, Ферма, Паскаля и Гюйгенса (1629—1695). Точка зрения Карла Бойера (1949) сводится к тому, что эти идеи в середине XVII века витали в воздухе в ожидании того, что их кто-то систематизирует и обобщит[16]. По мнению Маргарет Барон (Margaret E. Baron) (1969), первооткрывателем следует признать Барроу, а Ньютон и Лейбниц лишь придали его идеям алгебраическую форму[17].

В письме Роберту Гуку от 15 февраля 1676 года Ньютон процитировал известное высказывание Бернара Шартрского: «Если я видел дальше других, то потому, что стоял на плечах гигантов»[18]. Иллюстрация из рукописи начала XV века.

Сохранилось довольно большое количество документов, относящихся к истории открытия Ньютоном дифференциального исчисления, называемого им методом флюксий (англ. Method of Fluxions) — то, что впоследствии стало основой современного математического анализа[комм. 3]. В блокноте Ньютона за 1699 год он пишет о том, что, проанализировав свои старые записи о расходах, он вспомнил, что незадолго до Рождества 1664 года он приобрёл важные математические труды того времени — «Miscellanies» Франса ван Схотена и «Геометрию» Декарта. Зимой 1664/5 года он изучал эти книги. В этот период в трудах Валлиса Ньютон открыл для себя метод бесконечных рядов. Летом, спасаясь от эпидемии чумы в родном поместье Вулсторп, он вычислил с их помощью площадь гиперболы. Несколько месяцев спустя Ньютон мог вычислять производные, и к лету 1665 года он выяснил, что интегрирование является обратной операцией по отношению к дифференцированию; примерно в это время Ньютон вводит понятие флюксии, обозначающее скорость изменения величины функции. Автобиографические заметки по этому поводу были изложены в переписке с французским беженцем-гугенотом в Лондоне Пьером Демэзо, в 1718 году начавшим работу над сборником писем учёных «Collection of Various Pieces on Philosophy, Natural Religion, History, Mathematics etc by Messrs Leibniz, Clarke, Newton and other famous Authors». Множество прочих документов подтверждает эту хронологию[20].

В конце октября Ньютон начал и через несколько недель завершил небольшое эссе «How to draw tangents to mechanical lines», в котором развил идею о представлении функции в декартовых координатах. Вскоре после этого в документе, датированном 13 ноября 1665 года, он формулирует правило вычисления производной функции многих переменных — достижение, повторённое Лейбницем через 19 лет. Следующая известная относящаяся к данной проблематике рукопись датируется маем 1666 года — в ней Ньютон связывает понятие флюксии со скоростью движения. В октябре того же года все более ранние работы были объединены в один трактат[21]. Написанную в 1669 году статью De analysi per aequationes numero terminorum infinitas («Об анализе уравнениями бесконечных рядов»), обнародованную в 1711 году[22], Ньютон предпочёл не публиковать. Он переслал эту статью своему учителю и другу Исааку Барроу, а тот показал её в июле 1669 года математику Джону Коллинзу (1625—1683), выступавшему, по выражению Ричарда Уэстфолла, в роли «математического импресарио», поддерживающего математическое сообщество Англии и Европы[23]. Последний снял с неё копию и отослал оригинал Ньютону. Такой подход соответствовал обычаям того времени — учёные по различным причинам не спешили с обнародованием своих трудов. В таких случаях эти труды сообщались только самым близким друзьям или отдавались на хранение в учёные общества; иногда даже сущность труда, главная формула, скрывалась в виде анаграммы[24]. Однако данная статья, важная для развития методов дифференцирования, не содержала указаний на метод флюксий и была фактически бесполезна в дальнейшей полемике о приоритете[25]. Специально посвящённый этому методу трактат «Treatise on the Methods of Series and Fluxion» (1671) был издан после смерти Ньютона в 1736 году. Он не был завершён, но его существование зафиксировано в переписке Ньютона[22]. 10 декабря 1672 года Ньютон написал Коллинзу письмо, которое дополняло его сочинение «De analysi», в нём же Ньютон признавал, что выведенные им формулы аналогичны полученным ранее Рене де Слюзом (1622—1685) и Иоганном Худде (1628—1704), а в развитии своего метода он следовал указаниям Ферма, Грегори и Барроу[26][27][28]:

Намёк на метод [флюксий] я получил из способа Ферма приведения касательных; применяя его к абстрактным уравнениям прямо и обратно, я сделал его общим. М-р Грегори и д-р Барроу применяли и улучшили этот метод проведения касательных. Одна моя статья послужила оказией для д-ра Барроу показать мне его метод касательных до включения его в 10-ю лекцию по геометрии. Ибо я — тот друг, о котором он там упоминает.

Таким образом, хотя с помощью сохранившихся документов Ньютон мог доказать свой приоритет, его труды не были известны к началу XVIII века широким кругам учёных. Причина того, почему он не депонировал свои изыскания в архивах Королевского общества или Кембриджского университета, была той же, по которой он опубликовал с задержкой свою теорию цвета. В 1676 году Ньютон писал Лейбницу через Генри Ольденбурга[29]:

… после того, как по поводу ката-диоптрического телескопа я послал к тебе письмо, в котором вкратце разъяснил своё представление о природе света, одно неожиданное обстоятельство побудило меня спешно написать тебе о напечатании этого письма. А возникшие тогда же под влиянием различных писем (излагавших возражения и другое) многочисленные запросы совершенно удержали меня от исполнения моего намерения и привели к тому, что я стал упрекать себя в неблагоразумии и в том, что в погоне за тенью я прежде потеряю столь существенную вещь, как своё спокойствие.

Оригинальный текст (англ.)[показатьскрыть]

…when I had sent to you a letter on the occasion of the reflecting telescope, in which I briefly explained my ideas about the nature of light, something unforeseen made me judge it necessary to write in haste to you about the printing of that letter. And then frequent interruptions at once were created by the letters of various people filled with objections and other matters, which quite changed my mind, and caused me to call myself imprudent because, in order to catch at a shadow, I had sacrificed my peace, a truly substantial thing.

По мнению английского историка науки Альфреда Холла, в этих объяснениях Ньютон был не вполне искренен и, скорее, был просто не готов предъявить свои идеи широкой научной общественности и развивать их далее в условиях конкуренции[30]. Существует также мнение, что Ньютон не мог в это время разрешить логические противоречия, связанные с понятием бесконечно малой величины[31]. Советский биограф Ньютона С. И. Вавилов полагает, что для английского учёного математика играла вспомогательную роль и изложение «Начал» в новом стиле ничего бы не добавило к научной ценности его главного труда, но сделало бы его непонятным для большинства учёных и подвергло дополнительным нападкам[32].

К 1684 году, когда вышла в свет первая работа Лейбница по дифференциальному исчислению, Ньютон по-прежнему не имел никакого подготовленного к печати серьёзного математического труда, и следующие его действия в этом направлении были связаны с Дэвидом Грегори (1659—1708), который на основе неопубликованных трудов своего дяди Джеймса Грегори (1638—1675) далеко продвинулся в технике суммирования рядов. Свою статью «A Geometrical Essay on the Measuring of Figure» Грегори отправил Ньютону в июне 1684 года, поскольку слышал, что тот сделал какие-то открытия в этой области математики. Фактически Грегори частично воспроизвёл выводы из ньютоновской работы «De analysi» 1669 года. Не желая заниматься этим вопросом, Ньютон ограничился утверждением о том, что всё, сообщённое Грегори, было ему известно как минимум 10 лет назад, о чём сохранилась переписка с Лейбницем. На некоторое время Ньютон занялся математикой, но написанная в этот период статья «Specimens of a Universal System of Mathematics» так никогда и не была опубликована. Следующие два с лишним года Ньютон посвятил работе над своим главным трудом, «Математическими началами натуральной философии»[33]. Два года спустя Грегори вывел основную теорему о вычислении площадей фигур, ограниченных кривыми, получив от шотландского математика Джона Крэга (ученика и друга Ньютона) ту же информацию, которая во втором из писем 1676 года была сообщена Лейбницу (см. ниже). Несмотря на предупреждение Крэга о том, что этот результат идентичен ранее полученному Ньютоном, Грегори опубликовал свою теорему без упоминания имени Ньютона. Ньютон не сразу получил информацию об этой статье, но в 1691 году Грегори написал Ньютону письмо с просьбой о помощи в публикации «своей» теоремы. Начав писать Грегори формальный ответ, Ньютон вскоре приступил к работе над отдельным трактатом о квадратурах. К 1692 году работа под названием «De quadratura curvarum» была практически готова, и её видел Никола Фатио де Дюилье, однако, как и в других случаях, до публикации дело не дошло. Частично «De quadratura curvarum» была опубликована в составе «Оптики» в 1704 году, когда идея интегрирования уже утратила свою новизну[34].

К началу 1670-х годов Лейбниц был плохо знаком с современными ему достижениями в математике, и, хотя он с увлечением относился к этой науке, его основные интересы были связаны с философией, логикой и юриспруденцией[35]. В начале 1673 года Лейбниц впервые посетил Лондон в составе Майнцкого посольства[36]. Англия в это время особенно привлекала его славой своих замечательных математиков и химиков, местом сбора которых было незадолго перед тем учреждённое Лондонское Королевское общество. Лейбниц ещё в Майнце вступил в переписку со своим соотечественником Генри Ольденбургом, занимавшим пост секретаря общества. Теперь Лейбниц познакомился с ним лично и через него с некоторыми другими членами общества, в том числе с химиком Робертом Бойлем. Однако Лейбниц не посетил ни Оксфорд, где проживал Джон Валлис, ни Кембридж, где жили Исаак Ньютон и Исаак Барроу. Так же не состоялась встреча с Джоном Коллинзом, который в то время болел[37]. Из математиков, по всей видимости, Лейбниц встретился только с Джоном Пеллом[38]. 29 января он присутствовал на заседании Общества, на котором было зачитано письмо де Слюза о касательных[39]. В этот же приезд Лейбниц, продемонстрировавший свой механический калькулятор, был избран в члены Королевского общества[40]. Среди математических книг, которые Лейбниц приобрёл в Лондоне, были лекции Барроу, и существуют различные мнения относительно влияния, которое они на него оказали. Согласно утверждению самого Лейбница, он не читал этот перегруженный диаграммами и сложный для восприятия труд[15]. По мнению А. Холла, он просмотрел книгу мельком, однако, анализируя геометрические построения Лейбница, немецкий историк математики Карл Герхардт пришёл к выводу, что основную идею тот позаимствовал у Барроу[41][комм. 4].

Вероятно, ещё до поездки в Лондон Лейбниц лично познакомился с некоторыми математиками, с которыми ранее только переписывался. Среди них были французы Антуан Арно и Пьер де Каркави и голландец Христиан Гюйгенс. Последний презентовал ему свой только что изданный труд о маятниках Horologium Oscillatorium. Осознание того, что его математического образования недостаточно для того, чтобы понять труд Гюйгенса, подтолкнуло Лейбница к углублённым занятиям математикой[43]. Достаточно быстро он получил значимые результаты по построению бесконечных рядов для вычисления площади круга, на основе которых была создана теория дифференциального и интегрального исчисления[44]. О ходе этой работы известно из опубликованной в 1849 году переписки Лейбница с Ольденбургом, который выступал и как непосредственный корреспондент Лейбница, и как посредник в переписке с Коллинзом. Сразу по возвращении в Париж Лейбниц встретился с французским математиком Жаком Озанамом (1640—1718), с которым обсуждал решение уравнений. В связи с этим у него возникли новые вопросы, которые Лейбниц задал Ольденбургу. 16 марта 1673 года он получил ответ, а в полученном 16 апреля 1673 года письме Коллинз через Ольденбурга подробно сообщал о достижениях английских математиков[45]. В этом письме имя Ньютона появлялось трижды, в том числе как изобретателя общего метода вычисления площадей любых фигур и определения их центров тяжести с помощью бесконечных рядов. Возможно, из этого письма Лейбниц впервые узнал имя Ньютона, хотя не исключено, что они общались ранее по поводу изобретённого Ньютоном телескопа и других связанных с оптикой вопросов. В дальнейшем математические навыки Лейбница быстро прогрессировали. Продолжая свои математические занятия под руководством Гюйгенса, он получил новые интересные результаты в суммировании бесконечных рядов, в частности в конце 1673 года выражение ${\displaystyle 1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+...={\frac {\pi }{4}}}$[комм. 5]. Несмотря на то, что якобы Джеймс Грегори доказал ранее невозможность решить задачу квадратуры круга алгебраически, Лейбниц и Гюйгенс считали данное разложение указанием на существование такого решения; об этом также было в письмах к Ольденбургу[47]. В продолжающейся переписке Лейбниц, в духе времени, стремился узнать больше, чем сообщал сам[40]. Часто Лейбниц подчёркивал слова «сообщаю вам», если желал, чтобы Ольденбург хранил в тайне то или другое известие о добытых им результатах. Из переписки видно, что исследования Лейбница происходили совершенно независимо от результатов, полученных Ньютоном, и что Лейбниц шёл к общей цели совершенно иным путём. Из переписки можно сделать вывод, что Лейбниц не был знаком с Коллинзом во время своей первой поездки в Лондон и не мог получить от него рукописного сочинения Ньютона, более того — что Лейбниц вообще ничего не знал о содержании этого сочинения[48].

Письмо с изложением результата о суммировании «кругового ряда» пришло Ольденбургу в октябре 1674 года, и, начиная с него, переписка Лейбница с английскими математиками приняла более серьёзный характер[49]. 8 декабря Ольденбург написал осторожный ответ, в котором намекал Лейбницу не питать в этой области больших надежд на свой приоритет. В этот момент они оба находились в сложной ситуации — Ольденбург не знал в точности, чего достигли в этом вопросе Грегори и Ньютон, а Лейбниц мог оказаться в двусмысленном положении, если бы опубликовал свой результат. При этом недавно имел место конфликт о приоритете между Валлисом и Гюйгенсом, в результате которого последний был исключён из Королевского общества. Впоследствии приоритет открытия «кругового ряда» был одним из пунктов обвинения Ньютона против Лейбница, так как Ньютон утверждал, что сделал своё открытие ещё в 1669 году, а Коллинзу сообщил о нём чуть позже. Через Коллинза об этом ряде узнали Слюз во Франции и Грегори. Таким образом, хотя Лейбниц открыл свой ряд независимо, он имел возможность узнать о нём из нескольких источников. Таким образом, к 1675 году переписка Лейбница с Ольденбургом вошла в стадию, когда она перестала приносить новую информацию её участникам. Когда Лейбниц в одном из писем задал вопрос, может ли кто-либо из английских математиков вычислить длину дуги эллипса или гиперболы, Ольденбург ждал три месяца, прежде чем ответил, что могут, но только приблизительно, хотя с любой заданной точностью — а более подробную информацию может предоставить прибывший в Париж математик-любитель Чирнхаус (1651—1708). Вероятно, англичане предполагали, что от Чирнхауса Лейбниц мог получить детальную картину о состоянии дел в английской математике. Однако, судя по записям Лейбница, его общение с Чирнхаусом в Париже было очень кратким и до ноября 1675 года не касалось математики[50]. В конце 1675 года Лейбниц готовился к отбытию в Ганновер и собирался опубликовать свои математические труды. На фоне войны Франции с Нидерландами осложнились его отношения с Гюйгенсом. К этому же времени относится примечательное письмо, в котором Лейбниц излагает Ольденбургу свою концепцию метанауки, призванной дать ответ на все вопросы, в которой его дифференциальный метод займёт своё место[51].

В мае 1675 года в Англию приехал молодой немецкий учёный Эренфрид фон Чирнхаус, который познакомился там со многими научными знаменитостями и около сентября отправился в Париж, где сошёлся очень близко с Лейбницем и занимался вместе с ним математикой[52]. В 1725 году, то есть после смерти Чирнхауса, было впервые высказано обвинение в том, что Лейбниц от него получил знаменитое письмо Ньютона к Коллинзу, написанное в 1672 году[53]. На некоторое время переписка Лейбница с английскими математиками прервалась. В октябре 1675 года умер Джеймс Грегори, Коллинз находился в сложном положении и опасался потерять работу (что и произошло летом следующего года), Ольденбург был вовлечён в спор между Ньютоном и континентальными критиками его теории света[54], а сам Ньютон большую часть времени посвящал своим алхимическим занятиям. В результате коммерческого провала книги Барроу книготорговцы отказались работать с математиками без денежного участия с их стороны, что сделало проблематичным появление новых книг в этой отрасли. Переписка Лейбница с Ольденбургом и Коллинзом возобновилась в мае 1676 года по инициативе англичан. В новом письме содержались разложения в ряд для синуса и косинуса, которые присылались ему годом ранее, о чём Лейбниц, видимо, забыл. По крайней мере, он попросил доказательство их вывода, которое ему было прислано. Осенью 1676 года Лейбниц принял предложение герцога Ганноверского Эрнста Августа занять место его библиотекаря и покинул Париж, в котором проживал с 1672 года. Он отправился в Ганновер через Англию и Голландию[55], проведя неделю в Лондоне в октябре 1676 года[56]. В это время английские корреспонденты Лейбница относились к нему с большим энтузиазмом. Коллинз писал о «восхитительном господине Лейбнице»; Ольденбург также отзывался о нём с энтузиазмом[57].

Первая страница статьи Г. В. Лейбница «Nova Methodus pro Maximis et Minimis», Acta Eruditorum, 1684 год

После того, как Коллинз и Ольденбург в мае 1676 года узнали о возобновившемся интересе Лейбница к математике, они начали собирать имеющиеся в их распоряжении документы и письма для пересылки. В пакет были включены имеющиеся в распоряжении Коллинза отчёты о достижениях Грегори и других английских математиков за последние несколько десятилетий — так называемая «Historiola» объёмом в 50 страниц. Тем временем Ольденбург обратил внимание Ньютона на успехи Лейбница, в результате чего Ньютон написал через него Лейбницу письмо, в котором, между прочим, сообщил о своём биноме. Ольденбург отправил письмо 26 июля и при этом в первый раз упомянул о письме Ньютона к Коллинзу от 10 декабря 1672 года. Первое письмо Ньютона Лейбницу — 11 страниц на латыни — было издано в третьем томе «Mathematical Works» Джона Валлиса с неверным указанием даты отправки — 6 июля. Впоследствии Ньютон неоднократно повторял эту ошибку, упрекая Лейбница в том, что он изучал письмо три недели, прежде чем дать ответ. Так же Ньютон ошибочно полагал, что с этим письмом Лейбницу была переслана «Historiola» (тогда она была отправлена в сокращённом и неточном переводе на латынь)[58], и таким образом Лейбниц работал с этим объёмным документом всё лето перед поездкой в Лондон. В действительности, Лейбниц получил письмо 16 августа и на следующий день отправил Ньютону обстоятельный ответ, в котором рассказал ему об изобретённом им дифференциальном исчислении, не сообщив, однако, подробностей[59]. Относительно того, насколько откровенен был в этом письме Ньютон, существуют противоположные точки зрения: биограф Лейбница Йозеф Хофманн полагает, что Ньютон сделал всё, чтобы не сообщить Лейбницу главного о своём методе флюксий, тогда как Альфред Холл связывает отсутствие некоторых подробностей с тем, что к этому времени у Ньютона просто не было должным образом подготовленных работ на эту тему[60].

В октябре 1676 года Лейбниц отправился вторично в Лондон, где провёл примерно неделю. Тогда ему удалось увидеть сочинение «De Analisi», которое Ньютон написал в 1669 году, и сделать выписки из него, которые были найдены в недатированных бумагах Лейбница. Но в этом извлечении Лейбниц везде употребляет собственные знаки интегрального и дифференциального исчисления, что может указывать на то, что он познакомился с сочинением Ньютона уже после того, как сделал своё изобретение. Возможно, он получил его от Ольденбурга во время своей второй поездки в Лондон. В эту краткую поездку Лейбниц наконец встретился с Коллинзом и получил полную версию «Historiola»[61]. Второе письмо Ньютона к Лейбницу, небольшой трактат в 19 страниц, было завершено 24 октября, однако Лейбниц его не успел получить. Оно пролежало у Ольденбурга до весны следующего года, пока тот не нашёл возможности переслать его в Ганновер. В этом письме Ньютон сообщает Лейбницу о своём изобретении, не вдаваясь в подробности. Главная формула сообщена в виде анаграммы. В ответ на это письмо Лейбниц через Ольденбурга излагает ему основания своего дифференциального исчисления, не сообщая, однако, о своём знакомстве с сочинением 1669 года и алгоритмом вычисления интегралов[62][63]. В ноябре 1676 года имела место переписка между Ньютоном и Коллинзом. Коллинз безуспешно пытался убедить Ньютона опубликовать свои труды по математическому анализу, в ответ на что Ньютон уверял в превосходстве своего метода над тем, который изобрёл Лейбниц. Ещё несколько месяцев спустя Коллинз сообщил Ньютону о визите Лейбница и о том, что обсуждались бумаги Грегори. О том, что Лейбниц видел бумаги Ньютона, Коллинз умолчал и умер в ноябре 1683 года, так и не сообщив[комм. 6]. На письмо Лейбница Ньютон не ответил, а в августе 1678 года умер Ольденбург, и на следующее десятилетие учёные прекратили общение[65].

Как и Ньютон, Лейбниц не спешил с распространением информации о своих открытиях. До публикации статьи Лейбница «Новый метод максимумов и минимумов, а также касательных, и простой способ их вычисления» в журнале «Acta eruditorum» в октябре 1684 года почти никто о его достижениях не знал. За этой краткой и мало кем понятой статьёй, в которой излагались основные правила дифференцирования[66], последовал ряд других на ту же тему[67]. Поскольку этот журнал не входил в число основных математических изданий своего времени, и поскольку никто не мог предположить интереса Ньютона к данной публикации Лейбница, её путь из Лейпцига в Кембридж занял около года. Ньютон сразу понял важность статьи и сопоставил её с перепиской 1676 года, для него было очевидно, что «метод флюксий» и «дифференциальное исчисление» отражают одну и ту же математическую идею[68]. В вышедших в 1687 году «Математических началах натуральной философии» Ньютон применил метод флюксий только единожды, при доказательстве Леммы II во второй книге («Момент произведения равен сумме моментов отдельных производителей, умноженных на показатели их степеней и коэффициенты»[69]), соответствующей правилу дифференцирования произведений. В дальнейшем изложении «моменты» практически не используются, и возможным объяснением введения данной леммы является добавление автобиографического замечания[70]:

Таким образом, в 1687 году Ньютон не претендовал на то, чтобы объяснить достижения Лейбница полученной от него информацией. Под «vice verca» здесь понималось обратное к дифференцированию интегрирование, то есть метод вычисления площадей фигур, ограниченных кривыми, — его Ньютон, согласно вышеприведённой цитате, также не сообщал Лейбницу. Более никаких шагов для защиты своего приоритета Ньютон не предпринял. По замечанию английского историка науки Тома Уайтсайда, в это время Ньютону не хватило решительности, проявив которую, он бы избежал огромных беспокойств четверть века спустя[71].

Исаак Ньютон около 1710 года. Портрет работы Дж. Торнхилла

Переход конфликта между Ньютоном и Лейбницем в публичное пространство произошёл благодаря швейцарскому математику Никола Фатио де Дюилье. В 18 лет этот уроженец Базеля прибыл в Париж, где работал в обсерватории Джованни Кассини. Два года спустя они вместе описали явление зодиакального света. В 1686 году Фатио де Дюилье познакомился с Якобом Бернулли и Христианом Гюйгенсом. Совместно с последним он занимался изучением касательных. В начале 1687 года Фатио де Дюилье приехал в Лондон, где познакомился со многими английскими математиками. В следующем году он был принят в Королевское общество, на одном из заседаний которого он познакомился с Ньютоном. Вскоре между ними возникла настолько тесная дружба, что американский историк Фрэнк Мэньюэл задним числом заподозрил в ней «мощное гомосексуальное чувство»[80][81]. Фатио де Дюилье имел возможность ознакомиться с подготавливаемым Ньютоном к публикации трактатом «De quadratura curvarum». Поскольку ещё ранее он через Гюйгенса узнал о работах Лейбница в области анализа, ему стало очевидно, что подходы обоих математиков к решению задач дифференцирования и интегрирования совпадают с точностью до обозначений. 28 декабря 1691 года Фатио де Дюилье пишет письмо Гюйгенсу, в котором впервые прозвучало обвинение Лейбница в плагиате. В феврале следующего года он развивает эту тему, указывая на факт переписки между Ньютоном и Лейбницем[82]. Одновременно с этим Джон Валлис, будучи сторонником отстаивания научного приоритета Англии, убеждал Ньютона обнародовать свои математические исследования и письма 1676 года. Не добившись ничего, он включил упоминание о методе флюксий во второй том своих «Математических трудов» в 1693 году. Там же Валлис изложил свою версию приоритета: метод Лейбница аналогичен методу Ньютона, хотя и является его ухудшенной копией; оба они основываются на методе Барроу, который, в свою очередь, восходит к разработанной самим Валлисом теории бесконечных рядов. Тем не менее, считает А. Холл, до 1695 года Ньютон не считал, что его права первооткрывателя были ущемлены. Более того, в этот период Ньютон и Лейбниц возобновили переписку, и Лейбниц сам просил Ньютона издать улучшенное издание «Начал». В 1696 году Лейбниц ознакомился с трудом Валлиса и отметил, что метод Ньютона находится в согласии с его[83]. Иоганн Бернулли также изучил книгу Валлиса и пришёл к другому выводу, что Ньютон мог создать свой метод на основе анализа Лейбница. Своими соображениями он поделился с Лейбницем, который вначале не был готов поддержать этот тезис[84].

К концу 1690-х годов в континентальной Европе по-прежнему никто не знал о достижениях Ньютона и, тем более, об их хронологии. Схолия к Лемме II в «Началах» не осталась незамеченной, но, например, П. Вариньон понял её в том смысле, что Ньютон был знаком с анализом Лейбница. В 1699 году Валлис издал третий том своих сочинений, в который вошли оба письма 1676 года, а также более ранние документы, доказывающие прогресс исследований Ньютона. В этом же году Фатио де Дюилье опубликовал трактат «Lineae brevissimi descentus investigatio geometrica duplex» («Двоякое геометрическое исследование линии кратчайшего спуска»), в котором вернулся к задаче о брахистохроне 1696 года. К этому времени он уже шесть лет не поддерживал отношений с Ньютоном, и нет оснований полагать, что тот был как-то причастен к появлению этого труда — однако Лейбниц, знавший об их дружбе, был в этом уверен[85]. В своём «Исследовании» Фатио де Дюилье прямо обвинил Лейбница в плагиате. Тот, в свою очередь, получив экземпляр статьи от Лопиталя[86], опубликовал в «Acta eruditorum» анонимную рецензию, в которой опроверг эти обвинения, заявив о знакомстве только с методом касательных Ньютона. Тогда же Лейбниц анонимно раскритиковал продемонстрированное Дэвидом Грегори решение задачи о цепной линии. Хотя это решение было действительно ошибочным, Лейбниц пошёл дальше и в лице Грегори сделал выводы об ошибочности теорий математиков школы Ньютона. Авторство Лейбница в этих двух статьях было доказано в 1711 году, что серьёзно отразилось на его репутации. В 1701 году был издан перечень ошибок в ньютоновских «Началах», и, хотя список был в действительности составлен самим Ньютоном и передан Гюйгенсу Фатио де Дюилье, в Англии были уверены в причастности Лейбница[87]. В такой обстановке Ньютон в 1702 году дал обещание своим друзьям опубликовать «Оптику» и ещё два математических трактата («De quadratura curvarum» и «Enumeratio linearum tertii ordinis»), что и было выполнено два года спустя. В предисловии он указал, что эти работы восходят к его заметкам 1670-х годов, давно известным Лейбницу. Согласно Ньютону, метод флюксий, использованный в «De quadratura» для вычисления квадратур, был разработан им ещё в 1665 году. В январе 1705 года в «Acta eruditorum» вышла анонимная рецензия, которая была, как в настоящее время известно, написана Лейбницем (сам Лейбниц в этом никогда не признавался, но Ньютон был уверен в его авторстве). В этой рецензии утверждалось, что флюксии Ньютона соответствуют понятию, использованному французским математиком Оноре Фабри (1607—1688), и более раннему методу Кавальери[88], а результаты Ньютона излагались в терминах дифференциалов Лейбница. Хотя явного обвинения в плагиате не прозвучало, многими (в том числе и Ньютоном) это было воспринято именно так[89]. В октябре 1708 года ученик Ньютона Джон Кейлл опроверг эти инсинуации в статье «On the Laws of Centripetal Force»:

Все они [эти теории] следуют ныне весьма знаменитой Арифметике Флюксий, которую г-н Ньютон, вне всякого сомнения, Первым Изобрёл, что легко может узнать каждый, кто прочтёт его Письма, опубликованные Валлисом; та же Арифметика под другим названием и с использованием другой нотации была, однако, позднее опубликована в Acta eruditorum г-ном Лейбницем.

Оригинальный текст (англ.)[показатьскрыть]

All of these [propositions] follow from the now highly celebrated Arithmetic of Fluxions which Mr. Newton, beyond all doubt, First Invented, as anyone who reads his Letters published by Wallis can easy determine; the same Arithmetic under a different name and using different notation was later published in the Acta eruditorum, however, by Mr. Leibniz

Причины, по которым Кейлл решил выступить на защиту Ньютона, не ясны[90]. Можно предположить, что это выступление имело отношение к более широкому контексту разногласий между английскими и континентальными учёными по вопросу о природе сил и устройстве вселенной[91]. Номер «Философских трудов Королевского общества» с этой статьёй был опубликован в 1709 году[комм. 8], и Ньютон позднее утверждал, что не знал об этом пассаже Кейлла. Однако, учитывая, что статья была предварительно зачитана на заседании Королевского общества 3 ноября 1708 года, это маловероятно. Необходимо отметить, что Кейлл был близок к кругу оксфордских друзей Ньютона. Неизвестно, когда Лейбниц ознакомился со статьёй Кейлла, но официальное письмо с протестом в Королевское общество он направил в марте 1711 года[93].

Готфрид Вильгельм Лейбниц, портрет ок. 1710 года

Кейлл фактически выразил общее мнение, сложившееся в научном сообществе Англии. Так, физик Джордж Чейни в своём вышедшем в 1703 году труде «Обратный метод флюксий» писал, что за последние 20-30 лет в математике не появилось ничего, что бы не было повторением или тривиальным следствием предшествующего открытия Ньютона. Ксенофобские взгляды Чейни, приписывавшего все научные достижения своего времени англичанам и замалчивавшего достижения континентальных учёных, были отмечены Иоганном Бернулли, причислившего Чейни и ему подобных к «обезьянам Ньютона». Отношение Лейбница к английским учёным также стало более негативным, и с этого времени в его переписке появляется тема принижения достижений Ньютона[94]. Следующие 5 лет стороны воздерживались от открытой борьбы. Лейбниц не вступал в спор с Чейни и Фатио де Дюилье, Ньютон набирал административный вес — возглавил Монетный двор, Королевское общество и стал рыцарем[95]. С 1708 года обсуждался архив Джона Коллинза, содержащий не известные до этого широкой научной общественности ранние работы Ньютона, в том числе «De analysi» 1669 года. Также там были письма, из которых следовало, что Лейбниц об этом труде знал — о чём никогда не упоминал. 31 января 1711 года, за два месяца до получения письма Лейбница, выдержки этого архива на заседании Королевского общества представил доктор Ричард Мид. Подборка материалов и предваряющее их вступление не оставляло никаких сомнений в приоритете Ньютона[96]. Лейбниц в своей анонимной рецензии на «De analysi», ничего не говоря о датах, заявил, что суть изложенного в этом трактате метода сводится к развитию методов исчерпывания Архимеда и бесконечно малых Ферма. При этом в публичных заявлениях Лейбниц всегда высказывался о Ньютоне с большой почтительностью. Таким образом, вплоть до 1711 года оба участника конфликта воздерживались от прямых нападок друг на друга, действуя через своих сторонников[97].

Письмо с опровержением «дерзких обвинений» (англ. impertinent accusations) Кейлла было получено Королевским обществом 4 марта 1711 года. В нём Лейбниц выражал опасение, что эти обвинения будут повторяться бесчестными людьми, нанося ущерб его репутации. Поскольку оба они (Лейбниц и Кейлл) были членами Общества, Лейбниц потребовал, чтобы было дано официальное опровержение. Под председательством Ньютона 22 марта состоялось заседание Общества, на котором письмо было зачитано. Согласно протоколу, секретарю Общества Гансу Слоану было дано поручение составить ответ, однако этот документ не сохранился и вряд ли был вообще написан. Две недели спустя (15 апреля) вопрос был вновь рассмотрен и вновь под председательством Ньютона; на это заседание из Оксфорда прибыл Кейлл[98]. В протоколе собрания констатировалось, что в выпуске Acta eruditorum за 1705 год Лейбниц сделал ложное утверждение о сути математический достижений Ньютона и истинном их авторстве, на что было указано в своё время Кейллом. Неделю спустя Ньютон сделал приписку с упоминанием своих писем Коллинзу. Сохранились документы, свидетельствующие о бурной активности в эти недели — участники событий обменивались письмами, Ньютон перечитывал свои старые документы и восстанавливал в памяти хронологию событий. Составленный Кейллом окончательный ответ Лейбницу был утверждён на заседании Общества 24 мая. Предполагалось, что он будет опубликован, когда Лейбниц подтвердит получение, однако этого так и не произошло[99]. Лейбниц долго обдумывал свой ответ. Его письмо было отправлено 29 декабря и получено в Королевском обществе 31 января 1721 года. В нём Лейбниц избрал по отношению к Ньютону примирительный тон, не претендуя на его метод флюксий, схожий, однако, с его собственным методом. Первоначальной реакцией Ньютона, о чём свидетельствуют сохранившиеся черновики, было написать Слоану, что он не будет вступать в эту дискуссию. Однако постепенно эта тема увлекла его, особенно после того, как ему доставили вышедшую в феврале рецензию на «De analysi». Письма он так и не написал, но 6 марта 1712 года Королевское общество назначило комиссию для изучения писем и бумаг, относящихся к данному вопросу. В её состав вошли члены Общества математики Джон Арбетнот, Эдмунд Галлей, Уильям Джонс, Джон Мэчин, торговец и автор биографии Исаака Барроу Абрахам Хилл, чиновник Уильям Бёрнет. 17 апреля к ним присоединились политик Френсис Робартес, математики Абрахам де Муавр и Брук Тейлор, Френсис Астон и посол Пруссии Фредерик Бонет — по выражению Ньютона, это было «многочисленное и умелое собрание джентльменов нескольких наций»[100].

Работа комиссии не обещала быть очень сложной — Ньютон подготовил все материалы, добавив к архиву Коллинза письма Ольденбурга, 24 апреля он сам подготовил отчёт, который утверждал его собственные права как «первого автора» анализа. Лейбниц явно не обвинялся в плагиате, его виной указывалось нарушение научной этики, выразившееся в сокрытии факта использования известной ему информации[101]. На основе этого документа был подготовлен и издан в начале следующего года сборник «Commercium epistolicum D. Johannis Collis, et aliorum de analysi promota» («Переписка учёного Джона Коллинза и прочее относящееся к открытию анализа»). Издание вышло небольшим тиражом и не предназначалось для продажи. 25 копий было послано шотландскому книготорговцу в Гаагу и крупнейшим континентальным математикам, «способным судить о подобных вещах»[102]. «Commercium epistolicum» содержал ранее известные тексты, снабжённые пояснениями, акцентирующими внимание читателя на воровстве чужих идей, регулярно практикуемом, по мнению автора, Лейбницем. Новая линия доказательства, избранная Ньютоном, включала также утверждение, что свой метод флюксий он использовал в «Началах», что якобы подтверждали отправленные в 1683 году в Королевское общество фрагменты его незаконченного труда. Поскольку дата этого предполагаемого сообщения предшествовала публикации Лейбницем его первой статьи, это могло бы быть существенным обстоятельством, однако такого события в действительности не было[103]. Заключение комиссии Королевского общества гласило: «по этим основаниям мы считаем Ньютона первым изобретателем и думаем, что Кейлл, утверждая это, не сделал ничего несправедливого по отношению к Лейбницу»[104].

Общий эффект, произведённый публикацией «Commercium epistolicum», был огромен, и даже преданные сторонники Лейбница — Вариньон и Бернулли — были неприятно поражены тем, что их учитель почти 30 лет получал не вполне заслуженную славу[105]. Бернулли и Христиан Вольф убеждали Лейбница написать собственную версию истории математического анализа. Работа над этим трудом была начата в 1714 году, но не была закончена[106]. Не имея возможности опровергнуть аргументы Ньютона в вопросе о приоритете в открытии математического анализа или хотя бы доказать, что Лейбниц добился важных достижений до получения второго письма Ньютона, его критики атаковали по двум другим направлениям. Во-первых, подвергалась сомнению компетентность Ньютона как математика — сторонники Лейбница разыскивали ошибки в его трудах, прежде всего в «Математических началах натуральной философии». Наиболее последовательным критиком Ньютона в 1710-х годах был Иоганн Бернулли, большой резонанс имела обнаруженная его племянником Николаем Бернулли «ошибка» Ньютона в дифференцировании. Во-вторых, оспаривались положения ньютоновской теории тяготения. Для континентальных учёных, следовавших взглядам Декарта, вводимые Ньютоном взаимодействия через силы казались крайне сомнительными[107]. Все контраргументы были собраны и изданы в виде анонимной листовки, вошедшей в историю как «Charta Volans» (1713), в которой Лейбниц назывался единственным изобретателем анализа, производным от которого был метод Ньютона. Печатью и распространением этого памфлета занимался Христиан Вольф[108]. Осенью 1713 года через литератора Джона Чемберлейна документ попал в руки Ньютона, который вернулся к своей прежней пассивной тактике. Вероятно, он не считал необходимым реагировать на анонимные обвинения и ожидал более официального ответа на «Commercium epistolicum». Тем не менее, он считал, что какой-то ответ дать необходимо, раз уж Лейбниц сделал этот конфликт публичным. Эту миссию взял на себя Кейлл[109].

В номере за май — июнь 1713 года журнала «Journal littéraire de La Haye» Кейлл опубликовал большую статью об истории анализа, в котором для французской аудитории излагалась версия из «Commercium epistolicum», дополненная на основе обвинений Фатио де Дюилье. Из новых документов было опубликовано письмо Ньютона Коллинзу от 10 декабря 1672 года. В конце того же года Лейбниц дал ответ («Remarks on the Dispute», «Замечания о диспуте»), в котором заявил, что ничего не знал о претензиях Ньютона на приоритет до публикации «Commercium epistolicum» и ожидает, что Ньютон охладит пыл своих слишком рьяных сторонников. Также он отметил, что никогда не отдавал себя на суд Королевского общества, которому его точка зрения не была донесена. И, тогда как Ньютон скрыл свой метод, Лейбниц поступил противоположным образом. При этом собственный метод Ньютона был не так уж и хорош, как это было показано неким «известным математиком» (то есть Иоганном Бернулли). Вслед за этим была опубликована французская версия «Charta Volans». Таким образом, в дальнейшем Ньютону было необходимо доказывать не только свою историческую правоту, но также корректность своего метода; с тезисом о большем моральном праве Лейбница на открытие он спорить не мог[110]. Важнее всего для него было опровергнуть обвинения в совершении ошибок. Сохранился черновик письма, в котором Ньютон доказывает, что Лейбниц не понимает разницу между своими производными и его флюксиями — согласно современным представлениям эта разница практически неуловима. Летом 1714 года был опубликован «Ответ» Кейлла авторам «Замечаний» — по его мнению, под «известным математиком» имелся в виду Христиан Вольф[111]. Тем временем И. Бернулли, с одной стороны, хорошо изучил и высоко оценил ставшие известными работы Ньютона, с другой стороны, учитывая свою критику «ошибок» «Математических начал», опасался возможности исключения из Королевского общества. Соответственно этому он, по-прежнему поддерживая позицию Лейбница, предлагал ему внимательнее изучить «Commercium epistolicum»[112].

К середине 1714 года полемика выдохлась. Континентальная Европа в целом приняла сторону Лейбница — за исключением нидерландского журнала «Journal littéraire de La Haye», одним из редакторов которого был ньютонианец Вильгельм Якоб Гравезанд. Во Франции особое мнение высказал престарелый картезианец де Фонтенель, который отметил, что Лейбниц продолжил с того места, где остановился Барроу. Эта позиция была ближе к английской, и с течением времени, в силу политических и личных обстоятельств различных учёных, во Франции она стала усиливаться. Установление в Англии в 1714 году Ганноверской династии ничего не дало Лейбницу, который не смог заручиться поддержкой влиятельных политиков[113]. В последний период своей жизни Лейбниц оставил попытки доказать свой приоритет и сосредоточился на философских проблемах. Важнейшим эпизодом здесь была переписка с Сэмюелем Кларком по поводу философских основ физики, ставшая заочным спором с Ньютоном[114]. Со стороны Ньютона в 1715 году вышло две публикации: его собственная опубликованная анонимно статья «Account of the Book entitled Commercium Epistolicum … published by order of the Royal Society» («Отчёт о книге, озаглавленной „Commercium epistolicum“, изданной по распоряжению Королевского общества») и книга математика Джозефа Рафсона «История флюксий». Рафсон, не принадлежавший к кругу Ньютона, предпринял попытку исторического исследования вопроса о приоритете на основе доступных ему источников и пришёл к выводу, что Лейбниц смог получить ценную информацию из писем Ньютона. Его вердикт гласил: «Заимствовал ли Лейбниц метод, или изобрёл сам, не имеет абсолютного значения, ибо второй изобретатель не имеет прав»[104]. Ньютон, хотя и отрицал вначале свою заинтересованность в этом издании, после смерти Лейбница переиздал книгу без изменений[115]. «Отчёт», принадлежность которого перу Ньютона стала известна только в 1761 году, в очередной раз подробно суммировал разногласия с Лейбницем по пяти направлениям, начиная с истории математического анализа и его соотношения с методом флюксий и до философских вопросов. В Англии эта работа была принята как авторитетный источник, в Европе осталась практически незамеченной; в ноябре 1715 года вышел её французский перевод[116].

Лейбниц так никогда и не согласился признать приоритет Ньютона в изобретении математического анализа. Он также пытался написать собственную версию истории дифференциального исчисления, но, как и в случае с историей правителей Брауншвейга, не довёл дело до конца[117]. В конце 1715 года Лейбниц принял предложение Иоганна Бернулли устроить ещё одно соревнование математиков, в котором различные подходы должны были доказать свою состоятельность. На этот раз задача была взята из области, позднее названной вариационным исчислением, — требовалось построить касательную к семейству кривых. Письмо с формулировкой было написано 25 ноября и передано в Лондоне Ньютону через аббата Антонио Конти. Задача была сформулирована в не очень чётких терминах, и только позднее выяснилось, что требовалось найти общее, а не частное, как это понял Ньютон, решение. После того как англичане опубликовали своё решение, Лейбниц опубликовал своё, более общее, и, тем самым, формально победил в этом состязании[118]. Со своей стороны, Ньютон упорно стремился уничтожить своего оппонента. Не добившись этого с «Отчётом», он продолжил свои кропотливые изыскания, тратя на это сотни часов. Поводом для его следующего исследования, озаглавленного «Observations upon the preceding Epistle» («Наблюдения относительно предыдущего письма»), стало письмо Лейбница Конти от марта 1716 года, в котором критиковались философские взгляды Ньютона; новых фактов в этом документе приведено не было[119]. Со смертью Лейбница в ноябре 1716 года спор постепенно затих. По мнению А. Холла, после 1722 года этот вопрос перестал интересовать самого Ньютона[120].

В Англии в победе Ньютона в этом споре никогда не сомневались. Хотя негативные оценки роли Лейбница в англоязычной литературе встречались вплоть до XX века, уже во времена королевы Виктории начали звучать и другие мнения[121]. В 1920 году американский математик Артур Хэзевей, будучи уверен, что Лейбниц не мог самостоятельно сделать свои открытия, называл его основателем немецкого научного шпионажа, что, по его мнению, подтверждает случай с Дж. Пеллом (см. выше )[122]. К середине XX века страсти утихли, английские историки оценили заслуги Лейбница, а немецкие признали приоритет Ньютона[123].

Вопрос о сравнительных достоинствах нотаций дифференцирования Лейбница (${\displaystyle {\frac {dx}{dt}}}$) и Ньютона (${\displaystyle {\dot {x}}}$) обсуждался на протяжении XVIII века. Английская система была известна в континентальной Европе, но не очень популярна. В 1755 году Л. Эйлер отмечал неудобство обозначения производных высоких степеней, приводящее к нагромождению точек над знаком функции. Сравнительные исследования англичанина Р. Вудхауза (1802) и француза С. Лакруа (1810) также отдали предпочтение нотации Лейбница. Её успех окончательно закрепили усилия Дж. Гершеля, Дж. Пикока и Ч. Бэббиджа в Кембридже[124]. С научной точки зрения, по образному выражению Эрика Белла, «результатом всего этого [конфликта] было то, что упрямые британцы практически не продвинулись в математике в течение целого столетия после смерти Ньютона, в то время как более прогрессивные швейцарцы и французы, развивая идеи Лейбница и пользуясь его несравненно более удобным способом обозначений в анализе, усовершенствовали анализ и сделали его простым, легко применимым средством исследований, сделали то, что должны были сделать непосредственные последователи Ньютона»[125].

• И. Ньютон. Математические работы. — Гостехиздат, 1937. — 452 с.
• И. Ньютон. Математические начала натуральной философии / Пер. с латинского А. Н. Крылова, пред. Л. С. Полака. — М.: Наука, 1989. — 687 с. — 5000 экз.
• Briefwechsel zwischen Leibniz und Oldenburg, Collins, Newton... / H. C. I. Gerhardt. — Berlin: Asher, 1849.