Снелл, Виллеброрд
Ви́ллеброрд Снелл ван Ро́йен (нидерл. Willebrord Snel van Royen; 13 июня 1580, Лейден — 30 октября 1626, Лейден) — нидерландский математик, физик и астроном, ученик Людольфа ван Цейлена, профессор Лейденского университета. В части русских источников он именуется Снелль, Снеллий или Снел, печатался под латинизированным именем Снеллиус (Snellius).
| Виллеброрд Снелл ван Ройен | |
|---|---|
| Willebrord Snel van Royen | |
 | |
| Имя при рождении | нидерл. Willebrord Snel van Rayen |
| Дата рождения | 13 июня 1580[1], 1580[2] или 23 июня 1580[3] |
| Место рождения | |
| Дата смерти | 30 октября 1626[1][4][5][…] |
| Место смерти | |
| Страна | |
| Научная сфера | Математика, Физика, Астрономия |
| Место работы | Лейденский университет |
| Альма-матер | Лейденский университет |
| Научный руководитель | Людольф Цейлен Rudolph Snellius |
| Известен как | автор закона Снеллиуса |
Труды в области геометрии, тригонометрии, оптики и астрономии. Открыл закон преломления света («закон Снеллиуса»), лежащий в основании современной геометрической оптики. Первым применил триангуляцию для измерения длины земного меридиана, получил хорошую оценку радиуса Земли[6].
Биография

Родился в Лейдене в семье профессора математики Лейденского университета Рудольфа Снелла (1546—1613), став первым из троих его детей (двое других позднее умерли в детстве). Учился в Лейденском университете[6].
С 1600 года, вместе с Адрианом ван Роменом, путешествовал по различным европейским странам, в основном обсуждая астрономические проблемы. Проведя некоторое время в Вюрцбурге, два математика отправились в Прагу, где ван Ромен представил Снелла императорскому астроному Тихо Браге и Иоганну Кеплеру. Снелл провёл некоторое время с Браге, помогая ему проводить наблюдения, и, несомненно, он сам многому научился во время этого визита. Однако в октябре 1601 года Браге умер. Впоследствии Кеплер с глубоким уважением отзывался о Снелле (в трактате Stereometria doliorum, 1615) как о «всемирно прославленном геометре» (лат. geometrarum nostri seculi decus)[7].
Далее Снелл и ван Ромен поехали в Германию, где общались с Иоганном Преториусом, Михаэлем Мёстлином и другими учёными. Весной 1602 года Снелл ненадолго вернулся в Лейден, затем в 1603 году отправился в Париж, где продолжил изучение права, но также имел много контактов с математиками. После этого визита он бросил изучение права и из Лейдена почти не выезжал[6].

В 1604 году Снелл стал помогать отцу, здоровье которого ухудшилось, преподавать математику в университете. В этот период Снелл опубликовал комментарии работ Рамуса, а также переводы произведений Стевина и ван Цейлена. В 1608 году защитил диссертацию. В августе 1608 года он женился на Марии де Ланге, дочери бургомистра Схонховена[6]. Из их детей выжили трое[8].
В 1613 году, после смерти отца, занял его кафедру и, начиная с 1615 года, стал полноправным профессором Лейденского университета[9][10].
В 1626 году в возрасте 46 лет Снелл тяжело заболел и спустя две недели умер от некоей «колики», вызвавшей жар и паралич рук и ног. Похоронен 4 ноября в главной церкви Лейдена (Pieterskerk). Двадцать студентов несли его гроб[6].
Научная деятельность
В 1600-е годы Снелл сделал попытку реконструкции утерянных книг Аполлония Пергского (их содержание было кратко передано Паппом Александрийским). Результаты Снелл опубликовал в 1607—1608 годах; он подготовил реконструкцию ещё одной книги Аполлония, однако она не была опубликована и впоследствии затерялась[6].
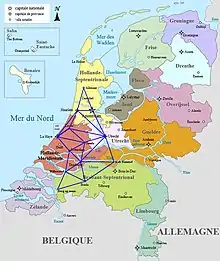
Снелл предложил использовать метод подобия треугольников для проведения геодезических измерений; при помощи этого метода он решил задачу, названную впоследствии «задачей Потенота»: найти точку, из которой стороны данного (плоского) треугольника видны под заданными углами. В своей работе «Eratosthenes Batavus» («Голландский Эратосфен», 1617 год), описывался метод триангуляции, который был открыт его соотечественником Геммой Фризиусом и стал, благодаря поддержке Снелла, широко используемым при съёмке и точном картографировании больших территорий[8].
В этой работе Снелл попытался измерить окружность Земли, что потребовало значительного количества измерений. Снелл взял за основу расстояние от своего дома до шпиля местной церкви, а затем построил систему треугольников, которая позволила ему определить расстояние между городами Алкмар и Берген-оп-Зомом, которое составляет около 130 км. Он выбрал эти города, поскольку они находились примерно на одном меридиане (современные данные дают Алкмару 4° 45' 0"' восточной долготы и Берген-оп-Зум 4° 18' 0" восточной долготы). Впервые в Европе Снелл ввёл важное понятие полярного треугольника[11]. Всего в сети из четырнадцати городов было выполнено 53 триангуляционных измерения; основными ориентирами всюду были церковные шпили.

Для точного выполнения измерений Снелл построил большой (210 см) квадрант, с помощью которого он мог измерять углы с точностью до десятых долей градуса. Этот квадрант до сих пор можно увидеть в Музее Бурхаве в Лейдене[6].
В результате своих расчётов Снелл получил хорошую оценку окружности Земли — в переводе на метрическую систему: 38653 км (ошибка 3,5 %). Снелл посвятил книгу Генеральным штатам, что было мудрым финансовым шагом, поскольку взамен они наградили его суммой, равной почти половине его годового оклада[6]. Снелл собирался расширить сеть городов, охваченных картографированием, но преждевременная смерть не позволила это сделать[8].
Часть трудов Снелла посвящены проблемам астрономии. Трактат Descriptio Cometae (1619) содержит его собственные наблюдения кометы, появившейся в ноябре 1618 года. В этой работе Снелл резко критиковал Аристотеля и подчёркивал, насколько вредно для развития науки продолжать относиться к его устаревшим взглядам с излишним почтением. Вместе с тем Снелл не принял гелиоцентрическую систему Коперника и твёрдо стоял на геоцентрических позициях.
В 1621 году Снелл описал закон преломления света. Однако ни этот, ни результаты других многочисленных экспериментов по оптике он опубликовать не успел. Исаак Восс в сочинении «Природа света» (De natura lucis, 1662) сообщил, что сын Виллеброда Снелла показывал ему рукопись сочинения отца, состоявшего из трёх книг; закон преломления там был выражен в следующей форме: «в одних и тех же средах отношение косекансов углов падения и преломления остаётся постоянным»[12].
Позже закон Снеллиуса был независимо открыт и опубликован Рене Декартом в трактате «Рассуждение о методе» (приложение «Диоптрика», 1637). Приоритет Снелла установил Христиан Гюйгенс в 1703 году, спустя 77 лет после смерти Снелла, когда этот закон уже был общеизвестен[6]. Недоброжелатели обвинили Декарта в плагиате, подозревая, что во время одного из своих визитов в Лейден Декарт услышал об открытии Снелла и смог ознакомиться с его рукописями[13]. Однако никаких доказательств плагиата нет, а самостоятельный путь Декарта к этому открытию подробно изучен историками[14].
В книге «Cyclometricus» (1621) Снелл приводит значение числа с 35 десятичными знаками. Для вычислений он использовал двойное неравенство[15]:
Первое из этих неравенств было знакомо уже в средние века Николаю Кузанскому.

В труде «Tiphys batavus» (1624), посвящённом актуальным для Нидерландов проблемам мореплавания, Снелл исследовал важную в теории навигации и картографии кривую на сфере, пересекающую все меридианы под постоянным углом. Он назвал её «локсодромой». Работа состояла из двух частей, одна из которых была теоретической, а другая посвящена практическим приложениям[6].
В изданном посмертно труде 1627 года Снелл внёс вклад в тригонометрию. В частности, впервые приведена формула для вычисления площади треугольника, когда известны длины двух сторон и угол между ними[16]: .
Память
В 1935 году Международный астрономический союз присвоил имя «Снеллиус» кратеру на видимой стороне Луны.
В честь учёного названы также:
- «Медаль Снеллиуса», присуждаемая Обществом содействия физике, медицине и хирургии (нидерл. Genootschap ter Bevordering van Natuur-, Genees- en Heelkunde) за работу в области естественных наук или математики, за исключением химии и биологии. Медаль учреждена в 1951 году и вручается раз в 10 лет[17].
- Антарктический «ледник Снеллиуса»[18].
- Одно за другим, три исследовательских корабля Королевских военно-морских сил Нидерландов (в 1929, 1952 и 2003 годах), последнее из них HNLMS Snellius (A802) продолжает находиться в строю[19].
Труды
 Eratosthenes Batavus (1617)
Eratosthenes Batavus (1617) Cyclometricus (1621)
Cyclometricus (1621).jpg.webp) Tiphys Batavus (1624)
Tiphys Batavus (1624)
- Apollonius batavus (Leiden, 1608)
- De re numeraria (Leiden, 1613)
- Eratosthenes Batavus : [лат.]. — Lugduni Batavorum : Joost van Colster, Joris Abrahamsz van der Marsce, 1617.
- Coeli et siderum in eo errantium observationes Hassicae : [лат.]. — Lugduni Batauorum : Joost van Colster, 1618.
- Descriptio cometae qui anno 1618 mense Novembri primum efjidsit (Leiden, 1619)
- Cyclometricus de ciratli dimensione : [лат.]. — Lugduni Batavorum : Matthijs Elzevier, Bonaventura Elzevier, 1621.
- Tiphys batavus (Leiden, 1624)
- Canon triangulorum (Leiden, 1626)
- Doctrinae triangulorum canonicae libri quatuor : [лат.]. — Lugduni Batavorum : Joannes Maire, 1627. Не закончена, издана посмертно, с дополнениями ученика Снелла Мартинуса Гортензиуса.
Участие как редактора:
- Petiias Ramus, Arithmetica. W. Snellius ed. (Leiden, 1613)
- Вильгельм IV (ландграф Гессен-Касселя). Coeli et siderum in eo errantium observationes Hassiacae, 1618.
- P. Rami. Meetkonst. Translated by Dirk Houtman, annotations by W. Snel (Amsterdam, 1622)
Примечания
- Архив по истории математики Мактьютор
- Leidse Hoogleraren (нидерл.)
- FINA Wiki — Австрийская академия наук.
- Willebrordus Snellius — 2009.
- Willebrord Snell // Encyclopædia Britannica (англ.)
- MacTutor.
- Nieuw Nederlandsch biografisch woordenboek.
- dwc.knaw.
- Храмов, 1983, с. 250.
- Математики. Механики, 1983, с. 443.
- Степанов Н. Н. Полярный сферический треугольник и его свойства // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 12—14. — 154 с.
- Розенбергер Ф. История физики. — М.—Л.: ГИТТЛ, 1934. — Т. 2. — С. 94—95.
- Снеллиус // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- История математики, том II, 1970, с. 32.
- Цейтен Г. Г. История математики в XVI и XVII веках / Обработка, примечания и предисловие М. Выгодского. — Изд. 2-е. — М.—Л.: ОНТИ, 1938. — С. 140. — 456 с.
- Юшкевич А. П. История математики в Средние века / Отв. ред. Б. А. Розенфельд; Академия наук СССР. Институт истории естествознания и техники. — М.: Физматгиз, 1961. — С. 286. — 448 с.
- Onderscheidingen
- Справочник на българските географски имена в Антарктика (болг.)
- Zr.Ms. Snellius
Литература
- Боголюбов А. Н. Снеллиус (Снелль ван Ройен) Виллеброрд // Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.
- Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — 468 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Храмов Ю. А. Снеллиус Виллеброрд (Snellius, Snell van Royen Villebrord) // Физики : Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и доп. — М. : Наука, 1983. — 400 с. — 200 000 экз.
Ссылки
- Статья на сайте «Элементы.ру»
- Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Снелл, Виллеброрд (англ.) — биография в архиве MacTutor.
- Snellius, Willebrord // Nieuw Nederlandsch biografisch woordenboek. Deel 7(1927) (нид.). Дата обращения: 22 июля 2021.
- WIllebrord Snel (Snellius), 1580—1626 (англ.). Дата обращения: 22 июля 2021.