Экспериментальная проверка специальной теории относительности
Специальная теория относительности — это физическая теория, играющая фундаментальную роль в описании всех физических явлений, когда гравитацией можно пренебречь. Многие эксперименты сыграли (и играют) важную роль в её разработке и обосновании. Предсказательная сила теории заключается в её уникальной способности правильно получать с высокой точностью результаты чрезвычайно разнообразных опытов. Повторы многих из этих экспериментов всё ещё проводятся с неуклонно возрастающей точностью, а современные опыты сосредоточены на эффектах, ожидаемых в планковских масштабах и в нейтринных исследованиях. Их результаты согласуются с предсказаниями специальной теории относительности. Сборники различных тестов предоставлены многими авторами: Якобом Лаубом[1], Чжаном[2], Маттингли[3], Клиффордом Уиллом[4]и Робертсом/Шлейфом[5].
Специальная теория относительности ограничена плоским пространством-временем, то есть всеми явлениями без значительного влияния гравитации. Последняя лежит в области общей теории относительности, и необходимо рассмотреть соответствующие проверки общей теории относительности.
Опыты, прокладывающие путь к теории относительности
Преобладающей теорией распространения света в 19 веке была теория светоносного эфира, стационарной среды, в которой свет движется аналогично тому, как звук в воздухе. По аналогии отсюда следует, что скорость света постоянна во всех направлениях в эфире и не зависит от скорости источника. Таким образом, наблюдатель, движущийся относительно эфира, должен измерять своего рода «эфирный ветер», точно так же, как наблюдатель, движущийся относительно воздуха, измеряет кажущийся ветер.
Опыты первого порядка
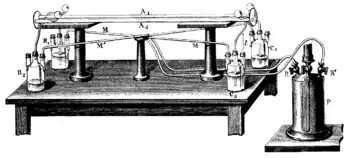
Начиная с работы Франсуа Араго (1810 г.), был проведён ряд оптических опытов, которые должны были дать положительный результат для величин до первого порядка по v/c и которые, таким образом, должны были продемонстрировать относительное движение эфира. И всё же результаты были отрицательными. Объяснение дал Огюстен Френель (1818 г.) введением вспомогательной гипотезы, так называемого «коэффициента увлечения», то есть материя увлекает эфир в незначительной степени. Этот коэффициент был непосредственно продемонстрирован экспериментом Физо (1851 г.). Позже было показано, что все оптические опыты первого порядка должны давать отрицательный результат из-за этого коэффициента. Кроме того, были проведены некоторые электростатические эксперименты первого порядка, которые снова дали отрицательные результаты. В целом Хендрик Лоренц (1892, 1895) ввёл несколько новых вспомогательных переменных для движущихся наблюдателей, продемонстрировав, почему все оптические и электростатические опыты первого порядка дали нулевые результаты. Например, Лоренц предложил переменную местоположения, с помощью которой электростатические поля сокращаются на линии движения, и другую переменную («местное время»), с помощью которой временные координаты движущихся наблюдателей зависят от их текущего местоположения[1].
Опыты второго порядка
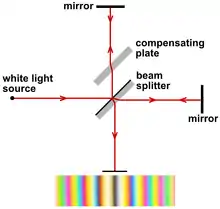
Однако теория стационарного эфира дала бы положительные результаты, если бы опыты были достаточно точными, чтобы измерять величины второго порядка по v/c. Альберт А. Майкельсон провёл первый опыт такого рода в 1881 году, а в 1887 году последовали более сложные измерения Майкельсона — Морли. Два луча света, идущие некоторое время в разных направлениях, были сведены в интерференционную картину, так что разная ориентация относительно эфирного ветра должна была привести к смещению интерференционных полос. Но результат снова оказался отрицательным. Выходом из этой дилеммы стало предположение Джорджа Фрэнсиса Фицджеральда (1889 г.) и Лоренца (1892 г.) о том, что материя сжимается по линии движения по отношению к эфиру (сокращение длины). То есть старая гипотеза о сжатии электростатических полей была распространена на межмолекулярные силы. Однако, поскольку для этого не было никаких теоретических оснований, гипотеза сжатия рассматривалась ad hoc.
Помимо оптического опыта Майкельсона — Морли, был также проведён его электродинамический эквивалент - эксперимент Траутона — Нобла. Тем самым он должен был показать, что на движущийся конденсатор должен действовать крутящий момент. Кроме того, опыты Рэлея и Брейса предназначались для измерения некоторых последствий сокращения длины в лабораторной системе отсчёта, например, предположения, что это приведёт к двулучепреломлению. Все эти эксперименты привели к отрицательным результатам. Проведённый в 1908 году опыт Троутона — Рэнкина также дал отрицательный результат при измерении влияния сокращения длины на электромагнитную катушку[1].
Для объяснения всех экспериментов, проведённых до 1904 года, Лоренц был вынужден снова расширить свою теорию, введя полное преобразование Лоренца. Анри Пуанкаре заявил в 1905 году, что невозможность демонстрации абсолютного движения (принцип относительности), по-видимому, является законом природы.
Опровержения полного эфирного увлечения
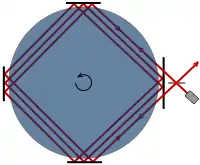
Идея о том, что эфир может быть полностью увлечён внутри или вблизи Земли, чем можно объяснить эксперименты с отрицательным эфирным дрейфом, была опровергнута множеством экспериментов.
- Оливер Лодж (1893 г.) обнаружил, что быстро вращающиеся стальные диски выше и ниже чувствительного интерферометра с общим оптическим путём не приводят к измеримому сдвигу полос.
- Густав Хаммар (1935) не смог найти никаких свидетельств увлечения эфира с помощью интерферометра с общими оптическими путями, одно плечо которого было заключено в толстостенную трубу, заполненную свинцом, а другое плечо — свободно.
- Эффект Саньяка показал, что эфирный ветер, вызванный сопротивлением земли, не может быть обнаружен.
- Существование аберрации света противоречило гипотезе увлечения эфиром.
- Предположение о том, что увлечение эфира пропорционально массе и, следовательно, имеет место только по отношению к Земле в целом, было опровергнуто опытом Майкельсона — Гэля — Пирсона, который продемонстрировал эффект Саньяка через движение Земли.
Лодж выразил парадоксальную ситуацию, в которой оказались физики, следующим образом: «…при практически невозможной скорости… материя [имеет] сколь-либо заметное вязкое сцепление с эфиром. Атомы должны быть в состоянии заставить его вибрировать, если они колеблются или вращаются с достаточной скоростью; иначе они не испускали бы света или какого-либо излучения; но ни в коем случае они не проявляются, чтобы увлечь его вместе с собой, или встретиться с сопротивлением при любом равномерном движении через него»[6].
Специальная теория относительности
Обзор
В конце концов Альберт Эйнштейн (1905) пришёл к выводу, что устоявшиеся теории и известные в то время факты образуют логическую связную систему только тогда, когда представления о пространстве и времени подвергаются фундаментальному пересмотру. Например:
- Электродинамика Максвелла — Лоренца (независимость скорости света от скорости источника),
- эксперименты с отрицательным эфирным ветром (без предпочтительной системы отсчета),
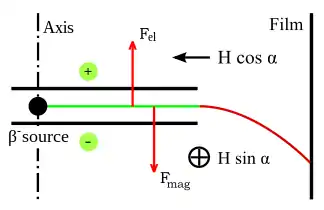
- Задача о движущемся магните и проводнике (актуально только относительное движение),
- опыт Физо и аберрация света (оба подразумевают добавление модифицированной скорости и отсутствие полного эфирного увлечения).
Результатом является специальная теория относительности, которая основана на постоянстве скорости света во всех инерциальных системах отсчета и принципе относительности. Здесь преобразования Лоренца больше не являются простым набором вспомогательных гипотез, но отражают фундаментальную симметрию Лоренца и составляют основу успешных теорий, таких как квантовая электродинамика. Специальная теория относительности предлагает большое количество проверяемых предсказаний, таких как[7]:
| Принцип относительности | Постоянство скорости света | замедление времени |
|---|---|---|
| Любой равномерно движущийся наблюдатель в инерциальной системе отсчета не может определить свое «абсолютное» состояние движения с помощью сопутствующей экспериментальной установки. | Во всех инерциальных системах отсчета измеренная скорость света одинакова во всех направлениях (изотропия), не зависит от скорости источника и не может быть достигнута массивными телами. | Скорость часов C (= любой периодический процесс), перемещающихся между двумя синхронизированными часами A и B, покоящимися в инерциальной системе отсчета, запаздывает по отношению к этим двум часам. |
| Также могут быть измерены другие релятивистские эффекты, такие как сокращение длины, эффект Доплера, аберрация и экспериментальные предсказания релятивистских теорий, таких как Стандартная модель. | ||
Фундаментальные опыты
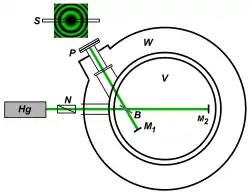
Эффекты специальной теории относительности можно феноменологически вывести из следующих трёх фундаментальных опытов[8]:
- Опытт Майкельсона — Морли, с помощью которого можно проверить зависимость скорости света от направления измерительного устройства. Он устанавливает соотношение между продольной и поперечной длинами движущихся тел.
- Опыт Кеннеди — Торндайка, с помощью которого можно проверить зависимость скорости света от скорости измерительного устройства. Он устанавливает связь между продольными длинами и продолжительностью времени движения тел.
- Опыт Ивеса — Стилвелла, с помощью которого можно напрямую проверить замедление времени.
Из этих трёх опытов и с использованием синхронизации Пуанкаре — Эйнштейна следуют преобразования Лоренца с — фактор Лоренца[8]:
Помимо вывода преобразования Лоренца, комбинация этих опытов также важна, потому что их можно интерпретировать по-разному, если рассматривать их по отдельности. Например, опыты по изотропии, такие как эксперименты Майкельсона — Морли, можно рассматривать как простое следствие принципа относительности, согласно которому любой наблюдатель, движущийся по инерции, может считать себя покоящимся. Таким образом, сам по себе опыт Майкельсона — Морли совместим с галилеевскими инвариантными теориями, такими как теория излучения или гипотеза полного увлечения эфиром, которые также содержат своего рода принцип относительности. Однако, когда рассматриваются другие опыты, исключающие галилеевские инвариантные теории (например, эксперимент Ивеса — Стилвелла, различные опровержения эмиссионных теорий и опровержения полного увлечения эфира), лоренц-инвариантные теории и, следовательно, специальная теория относительности остаются единственными теориями, которые оказываются жизнеспособными.
Интерферометры, резонаторы
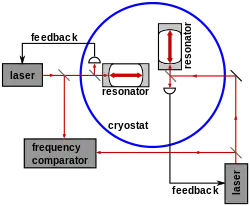
Современные варианты опытов Майкельсона — Морли и Кеннеди — Торндайка проводились для проверки изотропии скорости света. В отличие от Майкельсона — Морли, в экспериментах Кеннеди — Торндайка используются интерферометр с плечами разной длины, а измерения длятся несколько месяцев. Таким образом, можно наблюдать влияние различных скоростей во время обращения Земли вокруг Солнца. Используются лазерные, мазерные и оптические резонаторы, снижающие возможность любой анизотропии скорости света до уровня 10−17. В дополнение к наземным испытаниям также проводились опыты по лазерной дальнометрии Луны как разновидность эксперимента Кеннеди — Торндайка[4].
Другой тип опытов по изотропии — это эксперименты с ротором Мёссбауэра в 1960-х годах, с помощью которых можно наблюдать анизотропию эффекта Доплера на вращающемся диске с помощью эффекта Мёссбауэра (эти эксперименты также можно использовать для измерения замедления времени, см. Ниже).
Отсутствие зависимости от скорости источника или энергии
Баллистические теории, согласно которым скорость света зависит от скорости источника, предположительно могут объяснить отрицательный результат экспериментов по эфирному ветру. Только в середине 1960-х годов постоянство скорости света было окончательно доказано экспериментально, поскольку в 1965 году Дж. Г. Фокс показал, что эффекты теоремы погашения делают результаты всех предыдущих экспериментов неубедительными, и поэтому совместим как со специальной теорией относительности, так и с баллистической теорией[9][10]. Более поздние эксперименты определённо исключили баллистическую модель: самыми ранними были эксперименты Филиппаса и Фокса (1964)[11] с использованием движущихся источников гамма-излучения, а также эксперименты Альвегера и др. (1964)[12], которые показали, что фотоны не приобретают скорость быстро распадающихся мезонов, которые были их источником. Кроме того, эксперимент с системой двойных звёзд де Ситтера (1913 г.) повторил Брехер (1977 г.) с учётом теоремы о погашении, исключающей также зависимость от источника[13].
Наблюдения гамма-всплесков также показали, что скорость света не зависит от частоты и энергии световых лучей[14].
Одностороння скорость света
Была проведена серия односторонних измерений, и все они подтвердили изотропию скорости света[5]. Однако однозначно может быть измерена только двусторонняя скорость света (от А к В и обратно к А), поскольку односторонняя скорость зависит от определения одновременности и, следовательно, от метода синхронизации. Соглашение синхронизации Эйнштейна делает одностороннюю скорость равной двусторонней скорости. Однако существует множество моделей, имеющих изотропную двухстороннюю скорость света, в которых односторонняя скорость анизотропна за счёт выбора различных схем синхронизации. Они экспериментально эквивалентны специальной теории относительности, потому что все эти модели включают такие эффекты, как замедление времени движущихся часов, которые компенсируют любую измеримую анизотропию. Однако из всех моделей, имеющих изотропную двустороннюю скорость, для подавляющего большинства физиков приемлема только специальная теория относительности, поскольку все другие синхронизации гораздо сложнее, а эти другие модели (такие, как теория эфира Лоренца) основаны на крайних и неправдоподобных предположениях. относительно некоторых динамических эффектов, которые направлены на то, чтобы скрыть от наблюдения «предпочтительную систему отсчёта».
Изотропия массы, энергии и пространства
_in_D2O.gif)
Эксперименты по сравнению часов (периодические процессы и частоты можно рассматривать как часы), такие как эксперименты Хьюза — Древера, обеспечивают строгие экспериментальные проверки системы на лоренц-инвариантность. Они не ограничены фотонным сектором, как в опыте Майкельсона — Морли, но напрямую определяют любую анизотропию массы, энергии или пространства, измеряя основное состояние ядер. Получен верхний предел такой анизотропии 10−33 ГэВ. Таким образом, эти эксперименты являются одними из самых точных проверок лоренц-инвариантности, когда-либо проводившихся[3].
Замедление времени и сокращение длины

Поперечный эффект Доплера и, следовательно, замедление времени впервые непосредственно наблюдались в опыте Ивеса — Стилвелла (1938 г.). В современных экспериментах Ивеса — Стилвелла в накопительных кольцах тяжёлых ионов с использованием спектроскопии насыщения максимальное измеренное отклонение замедления времени от релятивистского предсказания было ограничено ≤ 10−8. Другие подтверждения замедления времени включают эксперименты с ротором Мёссбауэра, в которых гамма-лучи направлялись из середины вращающегося диска в приемник на краю диска, так что поперечный эффект Доплера можно было оценить с помощью эффекта Мёссбауэра. Путём измерения времени жизни мюонов в атмосфере и в ускорителях частиц также проверялось замедление времени движущихся частиц. С другой стороны, эксперимент Хафеле — Китинга подтвердил разрешение парадокса близнецов, то есть то, что часы, движущиеся от А к В обратно в А, отстают по сравнению с исходными часами. Однако в этом эксперименте эффекты общей теории относительности также играют существенную роль.
На практике трудно получить прямое подтверждение сокращения длины, поскольку размеры наблюдаемых частиц исчезающе малы. Однако есть косвенные подтверждения; например, поведение сталкивающихся тяжелых ионов можно объяснить, только если принять во внимание их повышенную плотность из-за лоренцевского сжатия. Сжатие также приводит к увеличению напряжённости кулоновского поля перпендикулярно направлению движения, эффекты которого уже наблюдались. Следовательно, при проведении экспериментов на ускорителях частиц необходимо учитывать как замедление времени, так и сокращение длины.
Релятивистский импульс и энергия
Начиная с 1901 г. был проведён ряд измерений, направленных на демонстрацию зависимости массы электронов от скорости. Результаты действительно показали такую зависимость, но точность, необходимая для различения конкурирующих теорий, долгое время оспаривалась. В конце концов стало возможным окончательно исключить все конкурирующие модели, кроме специальной теории относительности.
Сегодня предсказания специальной теории относительности регулярно подтверждаются на ускорителях частиц, таких как Релятивистский коллайдер тяжёлых ионов. Например, увеличение релятивистского импульса и энергии не только точно измеряется, но и необходимо для понимания поведения циклотронов, синхротронов и т. д., с помощью которых частицы разгоняются до скоростей, близких к скорости света.
Саньяк и Физо
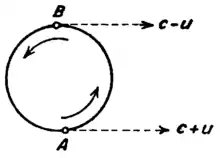
Специальная теория относительности также предсказывает, что два световых луча, движущихся в противоположных направлениях по вращающемуся замкнутому пути (например, петле), требуют разного времени пролёта, чтобы вернуться к движущемуся излучателю/приёмнику (это следствие независимости скорости света от скорости источника), см. выше). Этот эффект действительно наблюдался и называется эффектом Саньяка. В настоящее время учёт этого эффекта необходим для многих экспериментальных установок и для корректного функционирования GPS.
Если такие эксперименты проводятся в движущихся средах (например, в воде или стеклянном оптическом волокне), необходимо также учитывать коэффициент увлечения Френеля, как показано в эксперименте Физо. Хотя этот эффект изначально понимался как свидетельство почти стационарного эфира или частичного сопротивления эфира, его можно легко объяснить специальной теорией относительности, используя закон сложения скоростей.
Тестовые теории
Было разработано несколько тестовых теорий для оценки возможного положительного результата в экспериментах с нарушением Лоренца путем добавления определённых параметров к стандартным уравнениям. К ним относятся структура Робертсона — Мансури — Сексла (RMS) и расширение стандартной модели (SME). RMS имеет три проверяемых параметра в отношении сокращения длины и замедления времени. Отсюда можно оценить любую анизотропию скорости света. С другой стороны, SME включает множество параметров нарушения Лоренца не только для специальной теории относительности, но и для Стандартной модели и общей теории относительности; таким образом, она имеет гораздо большее количество проверяемых параметров.
Другие современные тесты
В связи с разработками, касающимися различных моделей квантовой гравитации в последние годы, отклонения от лоренц-инвариантности (возможно, следующие из этих моделей) снова стали целью экспериментаторов. Поскольку «локальная лоренц-инвариантность» (LLI) также выполняется в свободно падающих системах отсчёта, опыты, касающиеся слабого принципа эквивалентности, также относятся к этому классу тестов. Результаты анализируются с помощью теорий тестирования (как упоминалось выше), таких как RMS или, что более важной, SME[3].
- Помимо упомянутых вариаций опытов Майкельсона — Морли и Кеннеди — Торндайка, продолжают проводиться эксперименты Хьюза — Древера для тестов изотропии в протонном и нейтронном секторах. Для обнаружения возможных отклонений в электронном секторе используются спин-поляризованные крутильные весы.
- Замедление времени подтверждается в накопительных кольцах тяжёлых ионов, таких как TSR в MPIK, наблюдением эффекта Доплера лития, и эти эксперименты действительны в электронном, протонном и фотонном секторах.
- В других экспериментах ловушки Пеннинга используются для наблюдения за отклонениями циклотронного движения и ларморовской прецессии в электростатических и магнитных полях.
- Возможные отклонения от СРТ-инвариантности (чьё нарушение также представляет собой нарушение лоренц-инвариантности) можно определить в экспериментах с нейтральными мезонами, ловушками Пеннинга и мюонами, см. Тесты Лоренц-инвариантности в антивеществе.
- Астрономические тесты проводятся в связи со временем полёта фотонов, где факторы, нарушающие Лоренц-инвариантность, могут вызвать аномальную дисперсию и двойное лучепреломление, приводящее к зависимости фотонов от энергии, частоты или поляризации.
- Что касается пороговой энергии для реакций далёких астрономических объектов, а также земных источников, нарушения Лоренца-инвариантности могут привести к изменению стандартных значений для процессов, следующих из этой энергии, таких как вакуумное черенковское излучение или модификации синхротронного излучения.
- Осцилляции нейтрино (см. Нарушающие Лоренц-инвариантность осцилляции нейтрино) и скорость нейтрино (см. измерения скорости нейтрино) исследуются на предмет возможных нарушений Лоренц-инвариантности.
- Другими кандидатами для астрономических наблюдений являются предел Грайзена — Зацепина — Кузьмина и диски Эйри. Последние исследуются, чтобы найти возможные отклонения лоренц-инвариантности, которые могут поменять фазы фотонов.
- Наблюдения в секторе Хиггса продолжаются.
Примечания
- Laub, Jakob (1910). “Über die experimentellen Grundlagen des Relativitätsprinzips”. Jahrbuch der Radioaktivität und Elektronik. 7: 405—463.
- Zhang, Yuan Zhong. Special Relativity and Its Experimental Foundations. — World Scientific, 1997. — ISBN 978-981-02-2749-4.
- Mattingly, David (2005). “Modern Tests of Lorentz Invariance”. Living Rev. Relativ. 8 (5): 5. arXiv:gr-qc/0502097. Bibcode:2005LRR.....8....5M. DOI:10.12942/lrr-2005-5. PMID 28163649.
- Will, C.M. Special Relativity: A Centenary Perspective // Poincare Seminar 2005 / T. Damour ; O. Darrigol ; B. Duplantier ; V. Rivasseau. — Basel : Birkhauser, 2005. — P. 33–58. — ISBN 978-3-7643-7435-8. — doi:10.1007/3-7643-7436-5_2.
- Roberts. What is the experimental basis of Special Relativity?. Usenet Physics FAQ. University of California, Riverside. Дата обращения: 31 октября 2010.
- Lodge, Oliver, Sir. The Ether of Space. — New York : Harper and Brothers, 1909.
- Lämmerzahl, C. (2005). “Special Relativity and Lorentz Invariance”. Annalen der Physik. 517 (1): 71—102. Bibcode:2005AnP...517...71L. DOI:10.1002/andp.200410127.
- Robertson, H. P. (1949). “Postulate versus Observation in the Special Theory of Relativity”. Reviews of Modern Physics. 21 (3): 378—382. Bibcode:1949RvMP...21..378R. DOI:10.1103/RevModPhys.21.378.
- Fox, J. G. (1965), Evidence Against Emission Theories, American Journal of Physics Т. 33 (1): 1–17, DOI 10.1119/1.1971219
- Martínez, Alberto A. (2004), Ritz, Einstein, and the Emission Hypothesis, Physics in Perspective Т. 6 (1): 4–28, DOI 10.1007/s00016-003-0195-6
- Filippas, T.A. (1964). “Velocity of Gamma Rays from a Moving Source”. Physical Review. 135 (4B): B1071–1075. Bibcode:1964PhRv..135.1071F. DOI:10.1103/PhysRev.135.B1071.
- Alväger, T.; Farley, F. J. M.; Kjellman, J. & Wallin, L. (1964), Test of the second postulate of special relativity in the GeV region, Physics Letters Т. 12 (3): 260–262, DOI 10.1016/0031-9163(64)91095-9
- Brecher, K. (1977). “Is the speed of light independent of the velocity of the source”. Physical Review Letters. 39 (17): 1051—1054. Bibcode:1977PhRvL..39.1051B. DOI:10.1103/PhysRevLett.39.1051.
- Fermi LAT Collaboration (2009). “A limit on the variation of the speed of light arising from quantum gravity effects”. Nature. 462 (7271): 331—334. arXiv:0908.1832. Bibcode:2009Natur.462..331A. DOI:10.1038/nature08574. PMID 19865083.