Опыт Троутона — Нобла
Опыт Троутона — Нобла был попыткой обнаружить движение Земли через эфир. Опыт проведён в 1901—1903 годах Фредерик Томас Троутон и H. R. Noble. Он был основан на предположении Джорджа Фитцджеральда, что заряженный плосопараллельный конденсатор движущийся через эфир должен ориентироваться перпендикулярно движению. Как и в более раннем эксперименте Майкельсона — Морли, Траутон и Нобл получили нулевой результат: нельзя было обнаружить никакого движения относительно эфира[1][2]. Этот нулевой результат был воспроизведён в последующих попытках с возрастающей точностью Рудольфом Томашеком (1925, 1926), Чейзом (1926, 1927) и Хейденом в 1994 году[3][4][5][6][7][8]. Теперь видно, что такие экспериментальные результаты, согласующиеся со специальной теорией относительности, отражают справедливость принципа относительности и отсутствие какой-либо абсолютной системы покоя (или эфира). Эксперимент является проверкой специальной теории относительности.
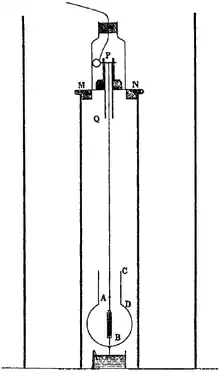
Опыт Траутона — Нобла также связан с мысленными экспериментами, такими как «парадокс Траутона — Нобла» и «прямоугольный рычаг» или «парадокс Льюиса — Толмена». Для решения этого парадокса было предложено несколько объяснений, и все они согласуются со специальной теорией относительности.
Опыт
В опыте подвешенный плоскопараллельный конденсатор удерживается тонким скрученным волокном и заряжается. Если бы теория эфира была верна, изменение уравнений Максвелла из-за движения Земли через эфир привело бы к крутящему моменту, заставляющему пластины выровняться перпендикулярно движению. Это можно записать в виде
где — крутящий момент, — энергия конденсатора, — угол между нормалью к пластине и скоростью.
С другой стороны, утверждение специальной теории относительности о том, что уравнения Максвелла инвариантны для всех систем отсчета, движущихся с постоянными скоростями, не предсказывает крутящего момента (нулевой результат). Таким образом, если эфир не закреплён каким-либо образом относительно Земли, то опыт является проверкой того, какое из этих двух описаний является более точным. Таким образом, его нулевой результат подтверждает лоренц-инвариантность специальной теории относительности.
Однако если отрицательный результат опыта легко объяснить в покоящейся системе отсчёта устройства, то объяснение с точки зрения подвижной системы отсчета (относительно вопроса о том, должен ли возникать такой же крутящий момент, как в «эфирной системе» описанный выше, или крутящий момент вообще не возникает) гораздо сложнее и называется «парадоксом Троутона — Нобла», который можно решить несколькими способами (см. решения ниже).
Парадокс прямого углового рычага
.png.webp)
Парадокс Троутона — Нобла по существу эквивалентен в мысленном эксперимент под названием «парадокс прямоугольного рычага», впервые рассмотрен Гилберт Ньютон Льюисом и Ричард Чейза Толменом в 1909 году[9]. Предположим, прямоугольный рычаг с концами обозначенными abc. В системе покоя силы в сторону ба и по направлению к bc должны быть равены для достижения равновесия, поэтому закон рычага не даёт крутящего момента:
где — это крутящий момент, и остаточная длина одного плеча рычага. Однако из-за сокращения длины ba длиннее, чем bc в недвижущейся системе, поэтому закон рычага даёт:
Видно, что крутящий момент не равен нулю, что, по-видимому, привело бы к вращению рычага в неподвижной системе координат. Поскольку вращение не наблюдается, Льюис и Толмен пришли к выводу, что крутящего момента не существует, поэтому:
Однако, как показал Макс фон Лауэ (1911)[10], это противоречит релятивистским выражениям для силы,
который даёт
Применительно к закону рычага возникает следующий крутящий момент:
Это принципиально та же проблема, что и в парадоксе Трутона — Нобла.
Решения
Подробный релятивистский анализ как парадокса Трутона — Нобла, так и парадокса прямоугольного рычага требует осторожности, чтобы правильно согласовать, например, эффекты, видимые наблюдателями в разных системах отсчёта, но в конечном итоге показано, что все такие теоретические описания дают один и тот же результат. В обоих случаях кажущийся результирующий крутящий момент на объекте (если смотреть из определённой системы отсчета) не приводит к какому-либо вращению объекта, и в обоих случаях это объясняется правильным релятивистским учётом преобразования всех соответствующих сил, импульсов и создаваемых ими ускорений. Ранняя история описаний этого эксперимента рассмотрена Янссеном (1995)[11].
Ток Лауэ
Первое решение парадокса Траутона — Нобла было дано Хендриком Лоренцем в 1904 году. Его результат основан на предположении, что крутящий момент и импульс из-за электростатических сил компенсируются крутящим моментом и импульсом из-за молекулярных сил[12].
Эта идея получила дальнейшее развитие в работе Макса фон Лауэ в 1911 году, который дал стандартное решение для такого рода парадоксов. В её основе лежала так называемая «инерция энергии» в её общей формулировке Макса Планка. Согласно Лауэ, энергетический поток, связанный с определённым импульсом («лауэвский ток»), возникает в движущихся телах за счёт упругих напряжений. Результирующий механический крутящий момент в случае эксперимента Траутона — Нобла имеет величину:
а в прямоугольном рычаге:
который точно компенсирует упомянутый выше электромагнитный момент, поэтому вращение не происходит в обоих случаях. Или другими словами: электромагнитный момент фактически необходим для равномерного движения тела, то есть для того, чтобы препятствовать вращению тела за счёт механического момента, вызванного упругими напряжениями[10][13][14][15].
С тех пор появилось много статей, в которых развивалось током Лауэ с некоторыми модификациями или переформулировками, а также включались различные варианты «скрытого» импульса[16].
Переформулировки силы и импульса
Других авторов не удовлетворяла идея о том, что крутящие моменты и противодействующие моменты возникают только потому, что выбираются разные инерциальные системы отсчёта. Их цель состояла в том, чтобы с самого начала заменить стандартные выражения для импульса и силы и, следовательно, равновесия явно лоренц-ковариантными. Таким образом, когда в покоящейся системе отсчёта рассматриваемого объекта нет крутящего момента, то нет крутящих моментов и в других системах[17]. Это аналогично проблеме 4/3 электромагнитной массы электронов, где аналогичные методы использовались Энрико Ферми (1921) и Фрицем Рорлихом (1960). В стандартной формулировке релятивистской динамики можно использовать гиперплоскости одновременности любого наблюдателя, в то время как в определении Ферми/Рорлиха следует использовать гиперплоскость одновременности системы покоя объекта[18]. По словам Янссена, выбор между стандартной моделью Лауэ и такими альтернативами является просто делом соглашения[18].
Следуя этой линии рассуждений, Рорлих (1966) различал «кажущиеся» и «истинные» преобразования Лоренца. Например, «истинное» преобразование длины будет результатом прямого применения преобразования Лоренца, которое даёт неодновременные положения конечных точек в другом кадре. С другой стороны, сокращение длины было бы примером кажущегося преобразования, поскольку одновременные положения конечных точек в движущейся системе отсчета должны быть рассчитаны в дополнение к начальному преобразованию Лоренца. Кроме того, Cavalleri/Salgarelli (1969) различали «синхронные» и «асинхронные» состояния равновесия. По их мнению, синхронный учёт сил следует использовать только для неподвижной системы отсчета объекта, а в движущихся системах те же силы следует учитывать асинхронно[19].
Сила и ускорение
Решение без компенсирующих сил или переопределений силы и равновесия было опубликовано Ричардом С. Толменом[20] и Полом Софусом Эпштейном[21][22] в 1911 году. Аналогичное решение было повторно обнаружено Франклином (2006)[23]. Они намекали на то, что сила и ускорение не всегда имеют одно и то же направление, то есть отношение массы, силы и ускорения имеет в теории относительности тензорный характер. Таким образом, роль, которую играет понятие силы в теории относительности, сильно отличается от роли в ньютоновской механике.
Эпштейн представил себе безмассовый стержень с концами OM, который закреплён в точке O, а в точке M закреплена частица с массой покоя m. Стержень охватывает угол с О. Теперь к ОМ приложена сила в точке М, и равновесие в его системе покоя достигается, когда . Как уже было показано выше, в неподвижной системе отсчёта эти силы имеют вид:
Таким образом
.
Тогда результирующая сила не направлена прямо от О к М. Приводит ли это к вращению стержня? Нет, потому что теперь Эпштейн рассмотрел ускорения, вызванные двумя силами. Релятивистские выражения для случая, когда масса m ускоряется этими двумя силами в продольном и поперечном направлениях, таковы:
- , где .
Таким образом
.
Тогда в этой системе также не происходит вращения. Аналогичные соображения также применимы к прямоугольному рычагу и парадоксу Траутона — Нобла. Таким образом, парадоксы разрешаются, поскольку два ускорения (в виде векторов) указывают на центр тяжести системы (конденсатора), а две силы — нет.
Эпштейн добавил, что если кто-то находит более удовлетворительным восстановить параллелизм между силой и ускорением, к которому мы привыкли в ньютоновской механике, он должен включить компенсирующую силу, которая формально соответствует току Лауэ. Эпштейн разработал такой формализм в последующих разделах своей статьи от 1911 года.
Примечания
- F. T. Trouton and H. R. Noble, "The mechanical forces acting on a charged electric condenser moving through space, " Phil. Trans. Royal Soc. A 202, 165—181 (1903).
- F. T. Trouton and H. R. Noble, "The Forces Acting on a Charged Condenser moving through Space. Proc. Royal Soc. 74 (479): 132—133 (1903).
- R. Tomaschek (1925). “Über Versuche zur Auffindung elektrodynamischer Wirkungen der Erdbewegung in großen Höhen I”. Annalen der Physik. 78 (24): 743&ndash, 756. Bibcode:1926AnP...383..743T. DOI:10.1002/andp.19263832403.
- R. Tomaschek (1926). “Über Versuche zur Auffindung elektrodynamischer Wirkungen der Erdbewegung in großen Höhen II”. Annalen der Physik. 80 (13): 509&ndash, 514. Bibcode:1926AnP...385..509T. DOI:10.1002/andp.19263851304.
- Carl T. Chase (1926). “A Repetition of the Trouton-Noble Ether Drift Experiment” (PDF). Physical Review. 28 (2): 378—383. Bibcode:1926PhRv...28..378C. DOI:10.1103/PhysRev.28.378.
- Carl T. Chase (1927). “The Trouton–Noble Ether Drift Experiment”. Physical Review. 30 (4): 516&ndash, 519. Bibcode:1927PhRv...30..516C. DOI:10.1103/PhysRev.30.516.
- R. Tomaschek (1927). “Bemerkung zu meinen Versuchen zur Auffindung elektrodynamischer Wirkungen in großen Höhen”. Annalen der Physik. 84 (17): 161&ndash, 162. Bibcode:1927AnP...389..161T. DOI:10.1002/andp.19273891709.
- H. C. Hayden (1994). “High sensitivity Trouton–Noble experiment”. Review of Scientific Instruments. 65 (4): 788&ndash, 792. Bibcode:1994RScI...65..788H. DOI:10.1063/1.1144955.
- Lewis, Gilbert N. (1909), The Principle of Relativity, and Non-Newtonian Mechanics, Proceedings of the American Academy of Arts and Sciences Т. 44 (25): 709–726, DOI 10.2307/20022495
- Laue, Max von (1911). “Ein Beispiel zur Dynamik der Relativitätstheorie”. Verhandlungen der Deutschen Physikalischen Gesellschaft. 13: 513—518.
- Janssen (1995), see «Further reading»
- Lorentz, Hendrik Antoon (1904), Electromagnetic phenomena in a system moving with any velocity smaller than that of light, Proceedings of the Royal Netherlands Academy of Arts and Sciences Т. 6: 809–831
- Laue, Max von (1911). “Zur Dynamik der Relativitätstheorie”. Annalen der Physik. 340 (8): 524—542. Bibcode:1911AnP...340..524L. DOI:10.1002/andp.19113400808.
- Laue, Max von (1911). “Bemerkungen zum Hebelgesetz in der Relativitätstheorie”. Physikalische Zeitschrift. 12: 1008—1010.
- Laue, Max von (1912). “Zur Theorie des Versuches von Trouton und Noble”. Annalen der Physik. 343 (7): 370—384. Bibcode:1912AnP...343..370L. DOI:10.1002/andp.19123430705.
- See «further reading», especially Nickerson/McAdory (1975), Singal (1993), Teukolsky (1996), Jefimenko (1999), Jackson (2004).
- See «further reading», for instance Butler (1968), Aranoff (1969, 1972), Grøn (1975), Janssen (1995, 2008), Ivezić (2006).
- Janssen (2008), see further reading
- Rohrlich (1967), Cavalleri/Salgarelli (1969)
- Tolman, Richard C. (1911), Non-Newtonian Mechanics :— The Direction of Force and Acceleration, Philosophical Magazine Т. 22: 458–463
- Epstein, P. S. (1911). “Über relativistische Statik”. Annalen der Physik. 341 (14): 779—795. Bibcode:1911AnP...341..779E. DOI:10.1002/andp.19113411404.
- Epstein, P. S. (1927). “Conference on the Michelson-Morley experiment”. Contributions from the Mount Wilson Observatory. 373: 45—49. Bibcode:1928CMWCI.373...43E.
- Franklin (2006, 2008), see «Further reading».
Литература
- История
- Michel Janssen, "A comparison between Lorentz's ether theory and special relativity in the light of the experiments of Trouton and Noble, Ph.D. thesis (1995). Online: TOC, pref., intro-I, 1, 2, intro-II, 3, 4, refs.
- Janssen, Michel H. P. (2008), Drawing the line between kinematics and dynamics in special relativity, Symposium on Time and Relativity Т. 40 (1): 1–76, doi:10.1016/j.shpsb.2008.06.004, <http://philsci-archive.pitt.edu/3895/>
- Учебники
- Tolman, R.C. (1917), The Right-Angled Lever, The theory of relativity of motion, Berkeley: University of California press, с. 539–776, 152–153
- Pauli, Wolfgang. Applications to special cases. Trouton's and Noble's experiment // Theory of Relativity. — New York : Dover, 1981. — P. 127–130. — ISBN 978-0-486-64152-2.
- Panofsky, Wolfgang. Classical electricity and magnetism / Panofsky, Wolfgang, Phillips, Melba. — Dover, 2005. — P. 274, 349. — ISBN 978-0-486-43924-2.
- Jackson, John D. Classical Electrodynamics. — 3rd. — Wiley, 1998. — ISBN 978-0-471-30932-1.
- Gamba, A. (1967). “Physical Quantities in Different Reference Systems According to Relativity”. American Journal of Physics. 35 (2): 83—89. Bibcode:1967AmJPh..35...83G. DOI:10.1119/1.1973974.
- Butler, J. W. (1968). “On the Trouton-Noble Experiment”. American Journal of Physics. 36 (11): 936—941. Bibcode:1968AmJPh..36..936B. CiteSeerX 10.1.1.144.9274. DOI:10.1119/1.1974358.
- Aranoff, S. (1969). “Torques and Angular Momentum on a System at Equilibrium in Special Relativity”. American Journal of Physics. 37 (4): 453—454. Bibcode:1969AmJPh..37..453A. DOI:10.1119/1.1975612.
- Furry, W. H. (1969). “Examples of Momentum Distributions in the Electromagnetic Field and in Matter”. American Journal of Physics. 37 (6): 621—636. Bibcode:1969AmJPh..37..621F. DOI:10.1119/1.1975729.
- Butler, J. W. (1969). “A Proposed Electromagnetic Momentum-Energy 4-Vector for Charged Bodies”. American Journal of Physics. 37 (12): 1258—1272. Bibcode:1969AmJPh..37.1258B. DOI:10.1119/1.1975297.
- Butler, J. W. (1970). “The Lewis-Tolman Lever Paradox”. American Journal of Physics. 38 (3): 360—368. Bibcode:1970AmJPh..38..360B. DOI:10.1119/1.1976326.
- Rohrlich, F. (1970). “Electromagnetic Momentum, Energy, and Mass”. American Journal of Physics. 38 (11): 1310—1316. Bibcode:1970AmJPh..38.1310R. DOI:10.1119/1.1976082.
- Sears, Francis W. (1972). “Another Relativistic Paradox”. American Journal of Physics. 40 (5): 771—773. Bibcode:1972AmJPh..40..771S. DOI:10.1119/1.1986643.
- Aranoff, S. (1973). “More on the Right-Angled Lever at Equilibrium in Special Relativity”. American Journal of Physics. 41 (9): 1108—1109. Bibcode:1973AmJPh..41.1108A. DOI:10.1119/1.1987485.
- Nickerson, J. Charles; McAdory, Robert T. (1975). “The Trouton-Noble paradox”. American Journal of Physics. 43 (7): 615—621. Bibcode:1975AmJPh..43..615N. DOI:10.1119/1.9761.
- Cavalleri, G.; Grøn, Ø.; Spavieri, G.; Spinelli, G. (1978). “Comment on the article "Right-angle lever paradox" by J. C. Nickerson and R. T. McAdory”. American Journal of Physics. 46 (1): 108—109. Bibcode:1978AmJPh..46..108C. DOI:10.1119/1.11106.
- Grøn, Ø. (1978). “Relativistics statics and F. W. Sears”. American Journal of Physics. 46 (3): 249—250. Bibcode:1978AmJPh..46..249G. DOI:10.1119/1.11164.
- Holstein, Barry R.; Swift, Arthur R. (1982). “Flexible string in special relativity”. American Journal of Physics. 50 (10): 887—889. Bibcode:1982AmJPh..50..887H. DOI:10.1119/1.13002.
- Singal, Ashok K. (1993). “On the "explanation" of the null results of Trouton-Noble experiment”. American Journal of Physics. 61 (5): 428—433. Bibcode:1993AmJPh..61..428S. DOI:10.1119/1.17236.
- Teukolsky, Saul A. (1996). “The explanation of the Trouton-Noble experiment revisited” (PDF). American Journal of Physics. 64 (9): 1104—1109. Bibcode:1996AmJPh..64.1104T. DOI:10.1119/1.18329.
- Jackson, J. D. (2004). “Torque or no torque? Simple charged particle motion observed in different inertial frames”. American Journal of Physics. 72 (12): 1484—1487. Bibcode:2004AmJPh..72.1484J. DOI:10.1119/1.1783902.
- Aguirregabiria, J. M.; Hernandez, A.; Rivas, M. (1982). “A Lewis-Tolman-like paradox”. European Journal of Physics. 3 (1): 30—33. Bibcode:1982EJPh....3...30A. DOI:10.1088/0143-0807/3/1/008.
- Franklin, Jerrold (2006). “The lack of rotation in the Trouton Noble experiment”. European Journal of Physics. 27 (5): 1251—1256. arXiv:physics/0603110. Bibcode:2006EJPh...27.1251F. DOI:10.1088/0143-0807/27/5/024.
- Franklin, Jerrold (2008). “The lack of rotation in a moving right angle lever”. European Journal of Physics. 29 (6): N55—N58. arXiv:0805.1196. Bibcode:2008EJPh...29...55F. DOI:10.1088/0143-0807/29/6/N01.
Journal of Physics A
- Jefimenko, Oleg D. (1999). “The Trouton-Noble paradox”. Journal of Physics A. 32 (20): 3755—3762. Bibcode:1999JPhA...32.3755J. DOI:10.1088/0305-4470/32/20/308.
Nuovo Cimento
- Arzeliès, H. (1965). “Sur le problème relativiste du levier coudé”. Il Nuovo Cimento. 35 (3): 783—791. Bibcode:1965NCim...35..783A. DOI:10.1007/BF02739341.
- Rohrlich, F. (1966). “True and apparent transformations, classical electrons, and relativistic thermodynamics”. Il Nuovo Cimento B. 45 (1): 76—83. Bibcode:1966NCimB..45...76R. DOI:10.1007/BF02710587.
- Newburgh, R. G. (1969). “The relativistic problem of the right-angled lever: The correctness of the Laue solution”. Il Nuovo Cimento B. 61 (2): 201—209. Bibcode:1969NCimB..61..201N. DOI:10.1007/BF02710928.
- Cavalleri, G.; Salgarelli, G. (1969). “Revision of the relativistic dynamics with variable rest mass and application to relativistic thermodynamics”. Il Nuovo Cimento A. 62 (3): 722—754. Bibcode:1969NCimA..62..722C. DOI:10.1007/BF02819595.
- Aranoff, S. (1972). “Equilibrium in special relativity” (PDF). Il Nuovo Cimento B. 10 (1): 155—171. Bibcode:1972NCimB..10..155A. DOI:10.1007/BF02911417. Архивировано из оригинала (PDF) 2012-03-28. Используется устаревший параметр
|url-status=(справка) - Grøn, Ø. (1973). “The asynchronous formulation of relativistic statics and thermodynamics”. Il Nuovo Cimento B. 17 (1): 141—165. Bibcode:1973NCimB..17..141G. DOI:10.1007/BF02906436.
- Pahor, S.; Strnad, J. (1974). “Statics in special relativity”. Il Nuovo Cimento B. 20 (1): 105—112. Bibcode:1974NCimB..20..105P. DOI:10.1007/BF02721111.
- Cavalleri, G.; Spavieri, G.; Spinelli, G. (1975). “Ropes and pulleys in special relativity (relativistic statics of threads)”. Il Nuovo Cimento B. 25 (1): 348—356. Bibcode:1975NCimB..25..348C. DOI:10.1007/BF02737685.
- Chamorro, A.; Hernández, A. (1978). “A synchronous formulation of relativistic statics”. Il Nuovo Cimento B. 41 (1): 236—244. Bibcode:1977NCimB..41..236C. DOI:10.1007/BF02726555.
- Hernández, A.; Rivas, M.; Aguirregabiria, J. M. (1982). “A quantitative analysis of the trouton-noble experiment”. Il Nuovo Cimento B. 72 (1): 1—12. Bibcode:1982NCimB..72....1H. DOI:10.1007/BF02894929.
- Ai, Hsiao-Bai (1993). “The historical misconception in relativistic statics”. Il Nuovo Cimento B. 108 (1): 7—15. Bibcode:1993NCimB.108....7A. DOI:10.1007/BF02874335.
- Nieves, L.; Rodriguez, M.; Spavieri, G.; Tonni, E. (2001). “An experiment of the Trouton-Noble type as a test of the differential form of Faraday's law”. Il Nuovo Cimento B. 116 (5): 585. Bibcode:2001NCimB.116..585N.
- Spavieri, G.; Gillies, G. T. (2003). “Fundamental tests of electrodynamic theories: Conceptual investigations of the Trouton-Noble and hidden momentum effects”. Il Nuovo Cimento B. 118 (3): 205. Bibcode:2003NCimB.118..205S.
Foundations of Physics
- Prokhovnik, S. J.; Kovács, K. P. (1985). “The application of special relativity to the right-angled lever”. Foundations of Physics. 15 (2): 167—173. Bibcode:1985FoPh...15..167P. DOI:10.1007/BF00735288.
- Spavieri, Gianfranco (1990). “Proposal for experiments to detect the missing torque in special relativity”. Foundations of Physics Letters. 3 (3): 291—302. Bibcode:1990FoPhL...3..291S. DOI:10.1007/BF00666019.
- Ivezić, Tomislav (2005). “Axiomatic Geometric Formulation of Electromagnetism with Only One Axiom: The Field Equation for the Bivector Field F with an Explanation of the Trouton-Noble Experiment”. Foundations of Physics Letters. 18 (5): 401—429. arXiv:physics/0412167. Bibcode:2005FoPhL..18..401I. DOI:10.1007/s10702-005-7533-7.
- Ivezić, Tomislav (2006). “Four-Dimensional Geometric Quantities versus the Usual Three-Dimensional Quantities: The Resolution of Jackson's Paradox”. Foundations of Physics. 36 (10): 1511—1534. arXiv:physics/0602105. Bibcode:2006FoPh...36.1511I. DOI:10.1007/s10701-006-9071-y.
- Ivezić, Tomislav (2006). “Trouton Noble Paradox Revisited”. Foundations of Physics. 37 (4—5): 747—760. arXiv:physics/0606176. Bibcode:2007FoPh...37..747I. DOI:10.1007/s10701-007-9116-x.
Ссылки
- Kevin Brown, "Trouton-Noble and The Right-Angle Lever в MathPages.
- Michel Janssen, "The Trouton Experiment and E = mc2, " Эйнштейн для всех учебный курс UMN (2002).