Лоренц-фактор

Фа́ктор Ло́ренца, или ло́ренц-фа́ктор, га́мма-фа́ктор — безразмерная физическая величина, используемая в релятивистской кинематике, монотонно возрастающая положительная функция скорости. Названа по имени Г. А. Лоренца. Определяется как

${\displaystyle \gamma \equiv {\frac {1}{\sqrt {1-v^{2}/c^{2}}}},}$

где v — скорость, c — скорость света в вакууме.

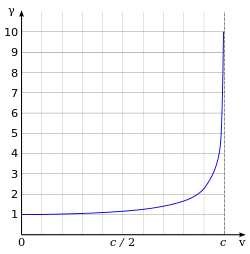
С увеличением скорости от 0 до c лоренц-фактор γ увеличивается от 1 до ${\displaystyle +\infty .}$

Связан с безразмерной скоростью β = v/c следующим образом:

${\displaystyle \gamma ={\frac {1}{\sqrt {1-\beta ^{2}}}},}$

${\displaystyle \beta ={\sqrt {1-{\frac {1}{\gamma ^{2}}}}}.}$

Лоренц-фактор равен гиперболическому косинусу быстроты φ:

${\displaystyle \gamma =\mathrm {ch} \,\varphi$ ;}

${\displaystyle \varphi =\mathrm {Arch} \,\gamma .}$

Собственное время частицы обратно пропорционально её лоренц-фактору. Время, измеряемое равномерно движущимися часами в данной инерциальной системе отсчёта, замедляется в γ раз. Если частица (часы) движется с переменной скоростью, её собственное время, прошедшее между событиями А и В на её мировой линии, равно:

${\displaystyle \tau =\int _{A}^{B}{\frac {dt}{\gamma (t)}}.}$

Например, собственное время мюона, летящего из верхних слоёв атмосферы со скоростью 0,99 от скорости света, замедляется по сравнению с координатным временем в ${\displaystyle \gamma ={\frac {1}{\sqrt {1-0,99^{2}}}}\approx 7}$ раз, в результате время жизни такого мюона оказывается в 7 раз длиннее времени жизни покоящегося мюона.

Релятивистское сокращение длины движущегося объекта пропорционально его лоренц-фактору. Так, в системе отсчёта вышеупомянутого мюона Земля движется со скоростью 0,99с, и в результате расстояние между верхними слоями атмосферы и поверхностью Земли сокращается в 7 раз.

Отношение полной энергии частицы к её массе равно лоренц-фактору (с точностью до множителя с²). В частности, полная энергия покоящейся частицы равна её массе, а для ультрарелятивистской частицы её масса пренебрежимо мала по сравнению с энергией (${\displaystyle \gamma \gg 1}$). Таким образом, полная энергия рассмотренного выше мюона (масса которого m_μ = 106 МэВ/c²) примерно равна 7m_μc² = 740 МэВ.