Среднее значение

Исходным пунктом становления теории средних величин явилось исследование пропорций школой Пифагора. При этом не проводилось строгого различия между понятиями средней величины и пропорции. Значительный толчок развитию теории пропорций с арифметической точки зрения был дан греческими математиками Никомахом Герасским (конец I — начало II в. н. э.) и Паппом Александрийским (III в. н. э.). Первым этапом развития этого понятия является этап, когда средняя стала считаться центральным членом непрерывной пропорции. Но понятие средней как центрального значения прогрессии не даёт возможности вывести понятие средней по отношению к последовательности n членов, независимо от того, в каком порядке они следуют друг за другом. Для этой цели необходимо прибегнуть к формальному обобщению средних. Следующий этап — переход от непрерывных пропорций к прогрессиям — арифметической, геометрической и гармонической[1].

В истории статистики впервые широкое употребление средних величин связано с именем английского учёного У. Петти. Он одним из первых пытался придать средней величине статистический смысл, связав её с экономическими категориями. Но описания понятия средней величины, его выделения, Петти не произвёл. Родоначальником теории средних величин принято считать А. Кетле. Он одним из первых начал последовательно разрабатывать теорию средних величин, пытаясь подвести под неё математическую базу. А. Кетле выделял два вида средних величин — собственно средние и средние арифметические. Собственно средние представляют вещь, число, действительно существующие. Собственно средние или средние статистические должны выводиться из явлений однокачественных, одинаковых по своему внутреннему значению. Средние арифметические — числа, дающие возможно близкое представление о многих числах, различных, хотя и однородных[2].

Каждый из видов средней может выступать либо в форме простой, либо в форме взвешенной средней. Правильность выбора формы средней вытекает из материальной природы объекта исследования. Формулы простых средних применяются в случае, если индивидуальные значения усредняемого признака не повторяются. Когда в практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторений индивидуальных значений признака присутствует в расчётных формулах степенных средних. В этом случае они называются формулами взвешенных средних.[3]

Изображение некоторых средних пары значений (n = 2) для a = x₁ и b = x₂:
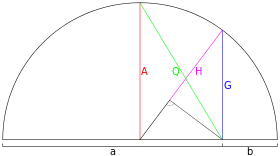
H = M₋₁(a, b) — гармоническое
G = M₀(a, b) — геометрическое
A = M₁(a, b) — арифметическое
Q = M₂(a, b) — квадратическое

• среднее значение функции — понятие, определяемое многими способами.
  • Более конкретно, но на основе произвольных функций, определяются средние Колмогорова для набора чисел.
    • среднее степенное — частный случай средних Колмогорова при ${\displaystyle \phi (x)=x^{\alpha }}$. Средние различных степеней связывает между собой неравенство о средних. Наиболее распространённые частные случаи:
      1. среднее арифметическое (${\displaystyle \alpha =1}$);
      2. среднее квадратическое (${\displaystyle \alpha =2}$);
      3. среднее гармоническое (${\displaystyle \alpha =-1}$);
      4. по непрерывности при ${\displaystyle \alpha \to 0}$ доопределяется среднее геометрическое, которое также является Колмогоровским средним при ${\displaystyle \phi (x)=\log x}$
• Среднее взвешенное — обобщение средней величины на случай неодинакового вклада усредняемых величин:
  • Среднее арифметическое взвешенное.
  • Среднее геометрическое взвешенное.
  • Среднее гармоническое взвешенное.
  • Среднее степенное взвешенное.
• среднее хронологическое — обобщает значения признака для одной и той же единицы или совокупности в целом, изменяющихся во времени.
• среднее логарифмическое, определяемое по формуле ${\textstyle {\bar {a}}={\frac {a_{1}-a_{2}}{\ln(a_{1}/a_{2})}}}$, используется в теплотехнике
• среднее логарифмическое, определяемое в электроизоляции в соответствии с ГОСТ 27905.4-88, определяется как ${\textstyle \log {\bar {a}}={\frac {\log a_{1}+\log a_{2}+\ldots +\log a_{n}}{a_{1}+a_{2}+\ldots +a_{n}}}}$ (логарифм по любому основанию)[4]

• непараметрические средние — мода, медиана.
• среднее значение случайной величины — то же, что математическое ожидание случайной величины. По сути — среднее значение её функции распределения.