Модель Пуанкаре в верхней полуплоскости

Модель Пуанкаре в верхней полуплоскости — это верхняя половина плоскости $\{(x,y)\mid y>0;x,y\in \mathbb {R} \}$ , обозначаемая ниже как H, вместе с метрикой (метрикой Пуанкаре), которая делает её моделью двумерной гиперболической геометрии (геометрии Лобачевского).

Параллельные лучи в модели Пуанкаре в верхней полуплоскости

Эквивалентно, модель Пуанкаре в верхней полуплоскости иногда описывается как комплексная плоскость, в которой мнимая компонента (координата y, упомянутая выше) положительна.

Модель Пуанкаре в верхней полуплоскости носит имя Анри Пуанкаре, но её создал Эудженио Бельтрами, который использовал её вместе с моделью Кляйна и моделью Пуанкаре́ в круге, чтобы показать, что гиперболическая геометрия настолько же непротиворечива, насколько непротиворечива евклидова геометрия.

Эта модель конформна, что означает, что углы, измеренные в точке модели, равны углам на гиперболической плоскости.

Преобразование Кэли даёт изометрию между моделью в полуплоскости и моделью Пуанкаре́ в круге.

Эту модель можно обобщить до модели (n+1)-мерного гиперболического пространства путём замены вещественного числа x вектором в n-мерном евклидовом векторном пространстве.

Метрика

Метрика модели в полуплоскости $\{\langle x,y\rangle |y>0\}$ имеет вид

(ds)^{2}={\frac {(dx)^{2}+(dy)^{2}}{y^{2}}}\,

,

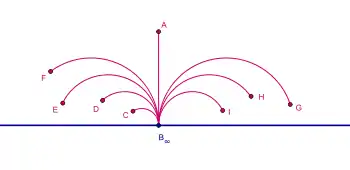
где s измеряет длину вдоль (возможно кривой) линии. Прямые на гиперболической плоскости (геодезические для этого метрического тензора, т.е. кривые, минимизирующие расстояние), представляются на этой модели дугами окружностей, перпендикулярными оси x (полуокружности с центром на оси x) и вертикальными лучами, перпендикулярными оси x.

Вычисление расстояния

В общем случае расстояние между двумя точками измеряется в этой метрике вдоль геодезических и равно:

{\begin{aligned}\operatorname {dist} (\langle x_{1},y_{1}\rangle ,\langle x_{2},y_{2}\rangle )&=\operatorname {arch} (1+{\frac {{(x_{2}-x_{1})}^{2}+{(y_{2}-y_{1})}^{2}}{2y_{1}y_{2}}})\\&=2\operatorname {arsh} {\frac {1}{2}}{\sqrt {\frac {{(x_{2}-x_{1})}^{2}+{(y_{2}-y_{1})}^{2}}{y_{1}y_{2}}}}\\&=2\ln {\frac {{\sqrt {{(x_{2}-x_{1})}^{2}+{(y_{2}-y_{1})}^{2}}}+{\sqrt {{(x_{2}-x_{1})}^{2}+{(y_{2}+y_{1})}^{2}}}}{2{\sqrt {y_{1}y_{2}}}}},\end{aligned}}

где arch и arsh — это обратные гиперболические функции

\operatorname {arsh} {x}=\ln \left(x+{\sqrt {x^{2}+1}}\right)\ ,\ \operatorname {arch} {x}=\ln \left(x+{\sqrt {x^{2}-1}}\right);x\geq 1\,.

Некоторые специальные случаи могут быть упрощены:

\operatorname {dist} (\langle x,y_{1}\rangle ,\langle x,y_{2}\rangle )=\left|\ln {\frac {y_{2}}{y_{1}}}\right|=|\ln(y_{2})-\ln(y_{1})|

[1].

\operatorname {dist} (\langle x_{1},y\rangle ,\langle x_{2},y\rangle )=\operatorname {arch} (1+{\frac {(x_{2}-x_{1})^{2}}{2y^{2}}})=2\operatorname {arsh} ({\frac {|x_{2}-x_{1}|}{2y}})

\operatorname {dist} (\langle x,r\rangle ,\langle x\pm r\sin \phi ,r\cos \phi \rangle )=\operatorname {arsh} (\tan \phi )=\operatorname {arch} ({\frac {1}{\cos \phi }})=\ln({\frac {1+\sin \phi }{\cos \phi }})

Другим способом вычисления расстояния между двумя точками является длина дуги вдоль (евклидовой) полуокружности:

\operatorname {dist} (AB)=\left|\ln \left({\frac {|BA_{\infty }|\ |AB_{\infty }|}{|AA_{\infty }|\ |BB_{\infty }|}}\right)\right|.

где $A_{\infty },B_{\infty }$ — точки полуокружности (концы), лежащие на граничной прямой, а $|PQ|$ — это евклидова длина сегмента окружности, соединяющей точки P и Q в этой модели.

Специальные точки и кривые

Бесконечно удалённые точки в модели Пуанкаре в верхней полуплоскости бывают двух типов:

точки на оси x
одна воображаемая точка на $y=\infty$ , которая является бесконечно удалённой точкой, через которую проходят все ортогональные оси x прямые.

Прямые, геодезические (кратчайшие пути между точками, находящимися на ней) моделируются

полуокружностями, концы которых находятся на оси x
Вертикальными лучами, ортогональными оси x

Окружности (кривые, равноудалённые от центральной точки) с центром в точке $(x,y)$ и радиусом $r$ моделируются:

окружностями с центром

(x,y\cosh(r))

и радиусом

y\sinh(r)

Гиперцикл (или эквидистанта, кривая, удалённая от гиперболической прямой, её оси или базы) моделируется

либо дугой окружности, которая пересекает ось x в тех же двух бесконечно удалённых точках, что и полуокружность, которая является базой, но имеет с осью x острый или тупой (не прямой) угол.
либо прямой, которая пересекает ось x в той же точке, что и вертикальный луч, который моделирует базу, но не перпендикулярной оси x.

Орицикл (предел семейства окружностей с общей касательной, проходящих через фиксированную точку и лежащих по одну сторону от этой касательной, образующийся при стремлении радиуса этих окружностей к бесконечности) моделируется

либо окружностью, касательной оси x (без бесконечно удалённой точки пересечения, которая является центром)
либо окружностью, параллельной x, в случае, если центром является бесконечно удалённой точкой с $y=\infty$ .

Краткий обзор евклидовых окружностей

Пусть дана евклидова окружность с центром $(x_{e},y_{e})$ и радиусом $r_{e}$ .

Если евклидова окружность полностью находится в верхней полуплоскости, она представляет гиперболическую окружность с центром $(x_{e},{\sqrt {y_{e}^{2}-r_{e}^{2}}})$ и радиусом ${\frac {1}{2}}\ln \left({\frac {y_{e}+r_{e}}{y_{e}-r_{e}}}\right)$ .
Если евклидова окружность полностью находится в верхней полуплоскости и касается границы, она представляет орицикл с центром в бесконечно удалённой точке c $(x_{e},0)$ .
Если окружность пересекает границу ортогонально ( $y_{e}=0$ ), она представляет гиперболическую прямую.
Если окружность пересекает границу не ортогонально, она представляет гиперцикл.

Построения с помощью циркуля и линейки

Здесь показывается, как производить построения с помощью циркуля и линейки в модели Пуанкаре[2]. Например, как построить полуокружность в евклидовой полуплоскости, которая моделирует гиперболическую прямую, проходящую через две точки.

Построение гиперболической прямой, проходящей через две точки

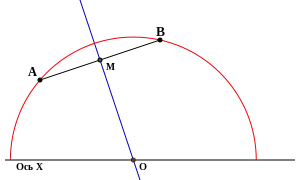
Построение прямой (красная), проходящей через две точки A и B.
M – середина отрезка.
O – центр полученной окружности (гиперболической прямой).

Строим отрезок, соединяющий две точки. Строим перпендикуляр, проходящий через середину отрезка. Находим пересечение этого перпендикуляра с осью x. Строим окружность с центром в точке пересечения, проходящую через данные точки (только верхнюю часть выше x).

Если эти две точки лежат на вертикальном луче, строим его (от оси x) , этот луч и будет искомой прямой.

Построение окружности с заданным центром, проходящей через точку

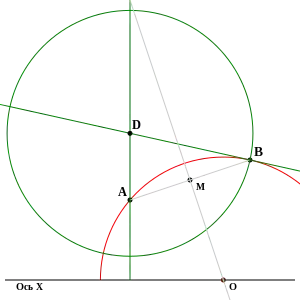
Построение окружности с центром в A, проходящей через точку B (случай, в котором точки A и B не лежат на одной вертикальной прямой).
Построение прямой, проходящей через A и B осуществляется как выше.
D – (евклидов) центр искомой окружности, гиперболическим центром той же окружности служит точка A.

Будем строить гиперболическую окружность с центром A, проходящую через точку B.

Если точки A и B не лежат на вертикальной прямой:

Строим гиперболическую прямую (полуокружность), проходящую через две заданные точки, как в предыдущем случае. Строим касательную к этой полуокружности в точке B. Проводим перпендикуляр к оси x через точку A. Находим пересечение этих двух прямых, чтобы получить центр D моделирующей окружности. Строим моделирующую окружность с центром в D, проходящую через заданную точку B.

Если точки A и B лежат на вертикальной прямой, и точка A лежит выше точки B:

Строим окружность вокруг пересечения вертикальной прямой и оси x, которая проходит через точку A. Строим горизонтальную прямую через точку B. Строим касательную к окружности в точке пересечения с этой горизонтальной прямой.

Середина отрезка между пересечением касательной с вертикальной прямой и B является центром моделирующей окружности. Строим моделирующую окружность вокруг центра, проходящую через точку B.

Если точки A и B лежат на вертикальной оси, и центр A лежит ниже точки B:

Строим окружность вокруг пересечения вертикальной прямой и осью x, которая проходит через заданный центр A. Строим касательную к окружности, проходящую через точку B. Строим горизонтальную прямую, проходящую через точку касания, и находим её пересечение с вертикальной прямой.

Средняя точка между полученной точкой пересечения и точкой является центром моделирующей окружности. Строим моделирующую окружность с новым центром и проходящую через точку B.

Найти центр заданной (гиперболической) окружности

Опускаем перпендикуляр p из евклидова центра окружности на ось x.

Пусть точка q является основанием этого перпендикуляра на ось x.

Строим прямую, касательную к окружности, проходящую через точку q.

Строим полуокружность h с центром в точке q, проходящую через точку касания.

Гиперболическим центром служит точка, в которой h и p пересекаются[3].

Группы симметрии

Звёздчатая правильная семиугольная мозаика модели

Проективная линейная группа PGL(2,C) действует на римановой сфере преобразованиями Мёбиуса. Подгруппа, которая отображает верхнюю половину плоскости H в себя — это PSL(2,R), состоящая из преобразований с вещественными коэффициентами, которая действует транзитивно и изометрично на верхней половине плоскости, что делает её однородным пространством.

Есть четыре тесно связанные группы Ли, которые действуют на верхнюю половину плоскости дробно-линейными преобразованиями, сохраняющими гиперболическое расстояние.

Специальная линейная группа SL(2,R), которая состоит из 2×2 матриц с вещественными элементами и определителем +1. Заметьте, что многие тексты (включая Википедию) часто упоминают SL(2,R), подразумевая под этим PSL(2,R).
Группа S*L(2,R), состоящая из 2×2 матриц с вещественными элементами с определителем +1 или −1. Заметим, что SL(2,R) является подгруппой этой группы.
Проективная специальная линейная группа PSL(2,R) = SL(2,R)/{±E}, состоящая из матриц из SL(2,R) по модулю ± единичной матрицы (то есть это факторгруппа по группе, состоящей из +E и -E).
Группа PS^*L(2,R) = S^*L(2,R)/{±E}=PGL(2,R) является снова проективной группой и, снова, по модулю ±E. PSL(2,R) содержится в ней в качестве нормальной подгруппы с индексом два; другой класс смежности состоит из матриц 2×2 с вещественными элементами и определителем −1, опять же по модулю ±E.

Связь этих групп с моделью Пуанкаре следующая:

Группа всех движений H, иногда обозначаемая как Isom(H), изоморфна PS^*L(2,R). Она включает как сохраняющие ориентацию движения, так и меняющие ориентацию. Меняющее ориентацию отображение (зеркальное отражение) — это $z\rightarrow -{\overline {z}}$ .
Группа сохраняющих ориентацию движений H, иногда обозначаемая как Isom⁺(H), изоморфна PSL(2,R).

Важными подгруппами группы изометрии являются фуксовы группы.

Часто рассматривается модулярная группа SL(2,Z), которая важна в двух аспектах. Во-первых, это группа линейных преобразований плоскости, сохраняющих решётку точек. Таким образом, функции, периодичные на квадратной решётке, такие как модулярные формы и эллиптические функции, наследуют симметрию решётки SL(2,Z). Во-вторых, SL(2,Z) является, конечно, подгруппой SL(2,R), а следовательно, имеет гиперболическое поведение, заложенное в ней. В частности, SL(2,Z) можно использовать для замощения гиперболической плоскости ячейками равной площади.

Изометрическая симметрия

Действие проективной специальной линейной группы PSL(2,R) на H определяется как

\left({\begin{matrix}a&b\\c&d\\\end{matrix}}\right)\cdot z={\frac {az+b}{cz+d}}={(ac|z|^{2}+bd+(ad+bc)\Re (z))+i(ad-bc)\Im (z) \over |cz+d|^{2}}.

Заметим, что действие транзитивно, поскольку для любых $z_{1},z_{2}\in \mathbb {H}$ существует элемент $g\in {\rm {PSL}}(2,\mathbb {R} )$ , такой, что $gz_{1}=z_{2}$ . Также верно, что если для всех z из H $gz=z$ , то g = e.

Стабилизатор или стационарная подгруппа элемента z из H — это множество $g\in {\rm {PSL}}(2,\mathbb {R} )$ , которые оставляют z неизменным — gz=z. Стабилизатор i — группа вращения

{\rm {SO}}(2)=\left\{\left({\begin{matrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{matrix}}\right)\,:\,\theta \in {\mathbf {R} }\right\}.

Поскольку любой элемент z из H отображается в i некоторым элементом PSL(2,R), это означает, что стационарная группа любого элемента z изоморфна SO(2). Таким образом, H = PSL(2,R)/SO(2). Также расслоение касательных векторов единичной длины на верхней половине плоскости, называемое единичным касательным расслоением, изоморфно PSL(2,R).

Верхняя половина плоскости замощается свободными регулярными множествами модулярной группой SL(2,Z).

Геодезические

Геодезические для метрического тензора являются полуокружностями с центрами на оси x и вертикальными лучами с началом на оси x.

Геодезические со скоростью единица, идущие вертикально через точку i, задаются выражением

\gamma (t)=\left({\begin{matrix}e^{t/2}&0\\0&e^{-t/2}\\\end{matrix}}\right)\cdot i=ie^{t}.

Поскольку PSL(2,R) действует транзитивно на верхней половине плоскости путём изометрий, эта геодезическая отображается в другие геодезические при помощи действия PSL(2,R). Таким образом, геодезическая общего вида с единичной скоростью задаётся как

\gamma (t)=\left({\begin{matrix}a&b\\c&d\\\end{matrix}}\right)\left({\begin{matrix}e^{t/2}&0\\0&e^{-t/2}\\\end{matrix}}\right)\cdot i={\frac {aie^{t}+b}{cie^{t}+d}}.

Это даёт полное описание геодезического потока расслоения касательных единичной длины (комплексное линейное расслоение) на верхней половине плоскости.

Модель в трёхмерных пространствах

Метрика модели в полупространстве

\{\langle x,y,z\rangle |z>0\}\,

задаётся выражением

(ds)^{2}={\frac {(dx)^{2}+(dy)^{2}+(dz)^{2}}{z^{2}}}\,

,

где s измеряет расстояние вдоль (возможно) кривой линии. Прямые в гиперболическом пространстве (геодезические для этого метрического тензора, т.е. кривые, которые минимизируют расстояние), представляются в этой модели дугами окружностей, исходящих перпендикулярно от плоскости z = 0 (полуокружности, центры которых находятся на плоскости z = 0) и лучами, исходящими перпендикулярно от плоскости z = 0.

Расстояние между двумя точками измеряется в этой метрике вдоль геодезической и равно

\operatorname {dist} (\langle x_{1},y_{1},z_{1}\rangle ,\langle x_{2},y_{2},z_{2}\rangle )=\operatorname {arch} \left(1+{\frac {{(x_{2}-x_{1})}^{2}+{(y_{2}-y_{1})}^{2}+{(z_{2}-z_{1})}^{2}}{2z_{1}z_{2}}}\right)=

=2\operatorname {arsh} \left({\frac {\sqrt {{(x_{2}-x_{1})}^{2}+{(y_{2}-y_{1})}^{2}+{(z_{2}-z_{1})}^{2}}}{2{\sqrt {z_{1}z_{2}}}}}\right)\,.

Модель в n-мерном пространстве

Модель можно обобщить до модели (n+1)-мерного пространства Лобачевского путём замены вещественных чисел x векторами в n-мерном евклидовом пространстве.

См.также

Примечания

mathematics stackexchange (неопр.). Дата обращения: 19 сентября 2015.
Bochaca, Judit Abardia Tools to work with the Half-Plane model (неопр.). Tools to work with the Half-Plane mode. Дата обращения: 25 июня 2015.
Cannon, Floyd, Kenyon, Parry, 1997, с. 87.

Литература

Cannon J. W., Floyd W. J., Kenyon R., Parry W. R. Figure 19. Constructing the hyperbolic center of a circle // Hyperbolic Geometry. — MSRI Publications, 1997. — Т. Volume 31. — (Flavors of Geometry).
Eugenio Beltrami. Teoria fondamentale degli spazi di curvatura constant // Annali. di Mat.. — 1868. — Т. 2. — С. 232–255.
Henri Poincaré. Théorie des Groupes Fuchsiens // Acta Mathematica. — 1882. — Т. 1. — С. 1. Первая статья в легендарной серии о модели в верхней полуплоскости.
Hershel M. Farkas, Irwin Kra. Riemann Surfaces. — New York: Springer-Verlag, 1980. — ISBN 0-387-90465-4.
Jurgen Jost. Section 2.3 // Compact Riemann Surfaces. — New York: Springer-Verlag, 2002. — ISBN 3-540-43299-X.
Saul Stahl. The Poincaré Half-Plane. — Jones and Bartlett, 1993. — ISBN 0-86720-298-X.
John Stillwell. Numbers and Geometry. — NY: Springer-Verlag, 1998. — С. 100–104. — ISBN 0-387-98289-2.. Элементарное введение в модель Пуанкаре.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] thematics stackexchange (неопр.). Дата обращения: 19 сентября 2015.

[2] Bochaca, Judit Abardia Tools to work with the Half-Plane model (неопр.). Tools to work with the Half-Plane mode. Дата обращения: 25 июня 2015.

[_26c809208c46f955-3] Cannon, Floyd, Kenyon, Parry, 1997, с. 87.