Обратные гиперболические функции

Обра́тные гиперболи́ческие фу́нкции (известные также как а̀реафу́нкции или ареа-функции) — семейство элементарных функций, определяющихся как обратные функции к гиперболическим функциям. Эти функции определяют площадь сектора единичной гиперболы x² − y² = 1 аналогично тому, как обратные тригонометрические функции определяют длину дуги единичной окружности x² + y² = 1. Для этих функций часто используются обозначения arcsinh, arcsh, arccosh, arcch и т.д., хотя такие обозначения являются, строго говоря, ошибочными, так как префикс arc является сокращением от arcus (дуга) и потому относится только к обратным тригонометрическим функциям, тогда как ar обозначает area — площадь. Более правильными являются обозначения arsinh, arsh и т.д. и названия обратный гиперболический синус, ареасинус и т.д. Также применяют[1] названия гиперболический ареасинус, гиперболический ареакосинус и т.д., но слово «гиперболический» здесь является лишним, поскольку на принадлежность функции семейству обратных гиперболических функций однозначно указывает префикс «ареа». Иногда названия соответствующих функций записывают через дефис: ареа-синус, ареа-косинус и т.д.

В комплексной плоскости гиперболические функции являются периодическими, а обратные им функции — многозначными. Поэтому подобно обратным тригонометрическим функциям обозначения ареафункций принято записывать с большой буквы, если подразумевается множество значений функции (логарифм в соответствующем определении функции также понимается как общее значение логарифма, обозначаемое Ln). С маленькой буквы записываются главные значения соответствующих функций.

В русской литературе обозначения большинства прямых и обратных гиперболических функций (так же как и части тригонометрических) отличаются от английских обозначений.

Название функции	Обозначение в русской литературе	Обозначение в английской литературе
ареасинус	arsh	arsinh, sinh⁻¹
ареакосинус	arch	arcosh, cosh⁻¹
ареатангенс	arth	artanh, tanh⁻¹
ареакотангенс	arcth	arcoth, coth⁻¹
ареасеканс	arsch, arsech	arsech, sech⁻¹
ареакосеканс	arcsch	arcsch, csch⁻¹

Определения функций

Ареасинус для действительного аргумента

Ареакосинус для действительного аргумента

Ареатангенс для действительного аргумента

Ареакотангенс для действительного аргумента

Ареасеканс для действительного аргумента

Ареакосеканс для действительного аргумента

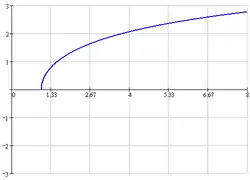
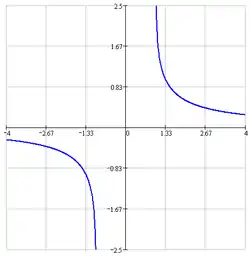
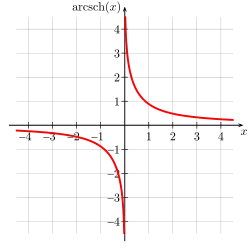
В комплексной плоскости главные значения функций можно определить формулами:

ареасинус

\operatorname {arsh} \,z=\ln(z+{\sqrt {z^{2}+1}}\,);

ареакосинус

\operatorname {arch} \,z=\ln(z+{\sqrt {z^{2}-1}});

ареатангенс

\operatorname {arth} \,z={\tfrac {1}{2}}\ln \left({\frac {1+z}{1-z}}\right);

ареакотангенс

\operatorname {arcth} \,z={\tfrac {1}{2}}\ln \left({\frac {z+1}{z-1}}\right);

ареасеканс

\operatorname {arsech} \,z=\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}-1}}\right);

ареакосеканс

\operatorname {arcsch} \,z=\ln \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}+1}}\,\right).

Квадратными корнями в этих формулах являются главные значения квадратного корня (то есть ${\sqrt {z}}={\sqrt {r}}\,e^{i\varphi /2},$ если представить комплексное число z как $z=re^{i\varphi }$ при $-\pi <\varphi \leq \pi$ ), а логарифмические функции являются функциями комплексной переменной. Для действительных аргументов можно осуществить некоторые упрощения, например ${\sqrt {x+1}}{\sqrt {x-1}}={\sqrt {x^{2}-1}},$ которые не всегда верны для главных значений квадратных корней.

Разложение в ряд

Обратные гиперболические функции можно разложить в ряды:

{\begin{aligned}\operatorname {arsh} \,x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n-1)!!}{(2n)!!}}\right){\frac {x^{2n+1}}{(2n+1)}},\qquad \left|x\right|<1.\end{aligned}}

{\begin{aligned}\operatorname {arch} \,x&=\ln 2x-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln 2x-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{(2n)}},\qquad x>1.\end{aligned}}

{\begin{aligned}\operatorname {arth} \,x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)}},\qquad \left|x\right|<1.\end{aligned}}

{\begin{aligned}\operatorname {arcsch} \,x=\operatorname {arsh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n+1)}}{(2n+1)}},\qquad \left|x\right|>1.\end{aligned}}

{\begin{aligned}\operatorname {arsech} \,x=\operatorname {arch} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1.\end{aligned}}

{\begin{aligned}\operatorname {arcth} \,x=\operatorname {arth} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3}}{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n+1)}}{(2n+1)}},\qquad \left|x\right|>1.\end{aligned}}

Асимптотическое разложение arsh x даётся формулой

\operatorname {arsh} \,x=\ln 2x+\sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\frac {\left({2n-1}\right)!!}{2n\left({2n}\right)!!}}}{\frac {1}{x^{2n}}}.

Производные

Функция $f(x)$	Производная $f'(x)$	Примечание
$\mathrm {arsh} \ x$	${\frac {1}{\sqrt {x^{2}+1}}}$	Доказательство $(arsh(x))'=(\ln {(x+{\sqrt {x^{2}+1}})})'={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot (x+{\sqrt {x^{2}+1}})'={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot ((x)'+({\sqrt {x^{2}+1}})')={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot (1+({\sqrt {x^{2}+1}})')={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot (1+{\frac {1}{2{\sqrt {x^{2}+1}}}}\cdot (x^{2}+1)')={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot (1+{\frac {2x}{2{\sqrt {x^{2}+1}}}})={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot ({\frac {x+{\sqrt {x^{2}+1}}}{\sqrt {x^{2}+1}}})={\frac {x+{\sqrt {x^{2}+1}}}{(x+{\sqrt {x^{2}+1}})\cdot ({\sqrt {x^{2}+1}})}}={\frac {1}{\sqrt {x^{2}+1}}}$
$\mathrm {arch} \ x$	${\frac {1}{\sqrt {x^{2}-1}}}$	Доказательство $(arch(x))'=(\ln {(x+{\sqrt {x^{2}-1}})})'={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot (x+{\sqrt {x^{2}-1}})'={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot ((x)'+({\sqrt {x^{2}-1}})')={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot (1+({\sqrt {x^{2}-1}})')={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot (1+{\frac {1}{2{\sqrt {x^{2}-1}}}}\cdot (x^{2}-1)')={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot (1+{\frac {2x}{2{\sqrt {x^{2}-1}}}})={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot ({\frac {x+{\sqrt {x^{2}-1}}}{\sqrt {x^{2}-1}}})={\frac {x+{\sqrt {x^{2}-1}}}{(x+{\sqrt {x^{2}-1}})\cdot ({\sqrt {x^{2}-1}})}}={\frac {1}{\sqrt {x^{2}-1}}}$
$\mathrm {arth} \ x$	${\frac {1}{1-x^{2}}}$	Доказательство $({\displaystyle \mathrm {arth} \ x})'={\biggl (}{\frac {1}{2}}\cdot \ln {\biggl (}{\frac {1+x}{1-x}}{\biggl )}{\biggl )}'={\frac {1}{2}}\cdot {\frac {1-x}{1+x}}\cdot {\biggl (}{\frac {1+x}{1-x}}{\biggl )}'={\frac {1}{2}}\cdot {\frac {1-x}{1+x}}\cdot {\frac {(1+x)'(1-x)-(1+x)(1-x)'}{(1-x)^{2}}}={\frac {1}{2}}\cdot {\frac {1-x}{1+x}}\cdot {\frac {2}{(1-x)^{2}}}={\frac {1}{1-x^{2}}}$
$\mathrm {arcth} \ x$	${\frac {1}{1-x^{2}}}$	Доказательство $({\displaystyle \mathrm {arcth} \ x})'={\biggl (}{\frac {1}{2}}\cdot \ln {\biggl (}{\frac {x+1}{x-1}}{\biggl )}{\biggl )}'={\frac {1}{2}}\cdot {\frac {x-1}{x+1}}\cdot {\biggl (}{\frac {x+1}{x-1}}{\biggl )}'={\frac {1}{2}}\cdot {\frac {x-1}{x+1}}\cdot {\frac {(x+1)'(x-1)-(x+1)(x-1)'}{(x-1)^{2}}}={\frac {1}{2}}\cdot {\frac {x-1}{x+1}}\cdot {\frac {-2}{(x-1)^{2}}}={\frac {1}{1-x^{2}}}$
$\mathrm {arsech} \ x$	$-{\frac {1}{x(x+1){\sqrt {\frac {1-x}{1+x}}}}}$
$\mathrm {arcsch} \ x$	$-{\frac {1}{x(x+1){\sqrt {1+{\frac {1}{x^{2}}}}}}}$

Для действительных x:

{\begin{aligned}{\frac {d}{dx}}\operatorname {arsech} \,x&{}=\mp {\frac {1}{x\,{\sqrt {1-x^{2}}}}};\qquad \Re \{x\}\gtrless 0.\\{\frac {d}{dx}}\operatorname {arcsch} \,x&{}=\mp {\frac {1}{x\,{\sqrt {1+x^{2}}}}};\qquad \Re \{x\}\gtrless 0.\end{aligned}}

Пример дифференцирования: если θ = arsh x, то:

{\frac {d\,\operatorname {arsh} \,x}{dx}}={\frac {d\theta }{d\operatorname {sh} \theta }}={\frac {1}{\operatorname {ch} \theta }}={\frac {1}{\sqrt {1+\operatorname {sh} ^{2}\theta }}}={\frac {1}{\sqrt {1+x^{2}}}}.

Комбинация гиперболических и обратных гиперболических функций

{\begin{aligned}&\operatorname {sh} (\operatorname {arch} \,x)={\sqrt {x^{2}-1}},\quad \quad |x|>1;\\&\operatorname {sh} (\operatorname {arth} \,x)={\frac {x}{\sqrt {1-x^{2}}}},\quad \quad -1<x<1;\\&\operatorname {ch} (\operatorname {arsh} \,x)={\sqrt {1+x^{2}}};\\&\operatorname {ch} (\operatorname {arth} \,x)={\frac {1}{\sqrt {1-x^{2}}}},\quad \quad -1<x<1;\\&\operatorname {th} (\operatorname {arsh} \,x)={\frac {x}{\sqrt {1+x^{2}}}};\\&\operatorname {th} (\operatorname {arch} \,x)={\frac {\sqrt {x^{2}-1}}{x}},\quad \quad |x|>1.\end{aligned}}

Дополнительные формулы

\operatorname {arsh} \;u\pm \operatorname {arsh} \;v=\operatorname {arsh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right).

\operatorname {arch} \;u\pm \operatorname {arch} \;v=\operatorname {arch} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right).

\operatorname {arth} \;u\pm \operatorname {arth} \;v=\operatorname {arth} \left({\frac {u\pm v}{1\pm uv}}\right).

{\begin{aligned}\operatorname {arsh} \;u+\operatorname {arch} \;v&=\operatorname {arsh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arch} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right).\end{aligned}}

{\begin{aligned}2\operatorname {arch} x&=\operatorname {arch} (2x^{2}-1),&\quad \quad x\geq 1;\\4\operatorname {arch} x&=\operatorname {arch} (8x^{4}-8x^{2}+1),&\quad \quad x\geq 1;\\2\operatorname {arsh} x&=\operatorname {arch} (2x^{2}+1),&\quad \quad x\geq 0;\\4\operatorname {arsh} x&=\operatorname {arch} (8x^{4}+8x^{2}+1),&\quad \quad x\geq 0.\\\end{aligned}}

См. также

Источники

М.Я. Выгодский. Справочник по высшей математике. — Наука, 1963. — С. 594. — 873 с.

Herbert Busemann, Paul J. Kelly (1953) Projective Geometry and Projective Metrics, с. 207, Academic Press.

Ссылки

Inverse hyperbolic functions на сайте MathWorld
Inverse hyperbolic functions

|Шаблон {{rq}} не предназначен для страниц из данного пространства имён.}}

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] М.Я. Выгодский. Справочник по высшей математике. — Наука, 1963. — С. 594. — 873 с.