Эклиптическая система координат
Эклиптическая система координат, или эклиптикальные координаты[1]:49 — это система небесных координат, в которой основной плоскостью является плоскость эклиптики, а полюсом — полюс эклиптики. Она применяется при наблюдениях за движением небесных тел Солнечной системы, плоскости орбит многих из которых, как известно, близки к плоскости эклиптики, а также при наблюдениях за видимым перемещением Солнца по небу за год[2]:30.
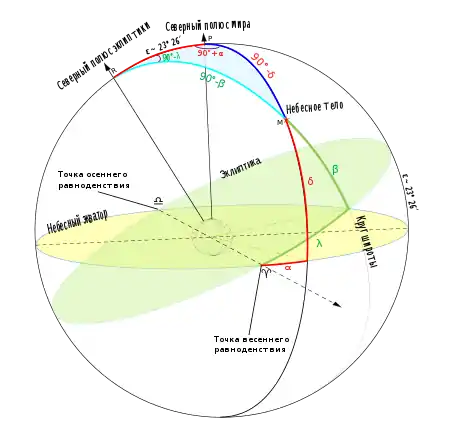
Описание
Одной координатой в этой системе является эклиптическая широта β, а другой — эклиптическая долгота λ.
Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.
Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.
Различают два типа эклиптических координат. В первом из них за центральную точку берётся центр Земли[3]. Эклиптическая геоцентрическая система координат используется в небесной механике для расчета орбиты Луны. Во втором центральной точкой считается центр Солнца[3]. Эклиптическая гелиоцентрическая система координат используется для расчета орбит планет и других тел Солнечной системы обращающихся вокруг Солнца.
Вследствие предварения равноденствий и колебания угла наклона плоскости эклиптики к небесному экватору, на продолжительных промежутках времени эклиптическая система координат не является фиксированной, в таких случаях необходимы ссылки на эпоху, то есть время, когда были измерены координаты[3].
Экваториальные координаты полюсов эклиптики на эпоху 1 января 2000 г.:
- Северный: прямое восхождение 18ч 0м 0.0с (точное значение), склонение +66° 33′ 38.55″ (созвездие Дракона)
- Южный: прямое восхождение 6ч 0м 0.0с (точное значение), склонение −66° 33′ 38.55″ (созвездие Золотой Рыбы).
Переход от второй экваториальной
Обозначим — прямое восхождение, — склонение, — угол наклона эклиптики к небесному экватору. Тогда формулы перехода от второй экваториальной системы координат к эклиптической системе координат имеют следующий вид:
Если косинусов и синусов недостаточно, и нужны сами и , их выражают из этих трёх формул: угол — из первой формулы, а угол — из второй и третьей формул. Причём для получения нужно разобраться со знаками. Обозначим правую часть второй формулы , а правую часть третьей — , тогда
Остаётся рассмотреть значения и , которые обращают в нуль:
- при и любом , и ;
- при и любом , и ;
- при и , и по формуле;
- при и , и по формуле.
Обозначим северный полюс эклиптики — , северный полюс мира — , положение данного небесного тела — и рассмотрим сферический треугольник . По теореме косинусов имеем:
Первая формула получена. Теперь к тому же сферическому треугольнику применяем теорему синусов:
Вторая формула получена. Теперь применяем к нашему сферическому треугольнику формулу пяти элементов[1]:67[4]:12:
Третья формула получена. Итак, все три формулы получены из рассмотрения одного сферического треугольника.
Переход ко второй экваториальной
Формулы перехода от эклиптической системы координат ко второй экваториальной системе координат имеют следующий вид. Обозначим — прямое восхождение, — склонение, — угол наклона эклиптики к небесному экватору. Тогда
Текущая эклиптическая долгота Солнца
339.79481607578°
Примечания
- Цесевич В.П. Что и как наблюдать на небе. — 6-е изд. — М.: Наука, 1984. — 304 с.
- Белова Н.А. Курс сферической астрономии. — М.: Недра, 1971. — 183 с.
- Небесные координаты — статья из Большой советской энциклопедии.
- Балк М.Б., Демин В.Г., Куницын А.Л. Сборник задач по небесной механике и космодинамике. — М.: Наука, 1972. — 336 с.
Литература
- Цесевич В.П. Что и как наблюдать на небе. — 6-е изд. — М.: Наука, 1984. — 304 с.
- Даффет-Смит П. Практическая астрономия с калькулятором. — М.: Мир, 1982. — 176 с.