Прямое восхождение
Прямое восхождение (α; также R. A. — от англ. right ascension) — координата объекта на небесной сфере, используемая во второй экваториальной системе координат. Прямое восхождение равно длине дуги небесного экватора от точки весеннего равноденствия до круга склонения светила, причём оно отсчитывается против часовой стрелки, если смотреть со стороны северного полюса мира[1].
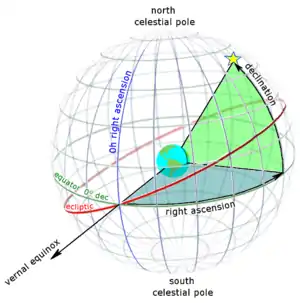
Прямое восхождение α вместе со склонением δ образуют вторую экваториальную систему координат — систему небесных координат, общепринятую в астрономии. Прямое восхождение удобно тем, что в отличие от часового угла и азимута не меняется из-за суточного движения.
Прямое восхождение обычно выражается либо в градусной мере (от 0° до 360°), либо в часовой мере (от 0h до 24h), причём 360° и 24h не включаются. Иногда часовые углы могут отсчитываться к востоку и к западу от точки весеннего равноденствия — по аналогии с долготой. В этом случае они принимают значения от −180° до +180°, или, в часовой мере, от −12h до +12h[1].
| Часовые меры | ||||
|---|---|---|---|---|
| Название | Символ | Значение | Градусная мера | Радианы |
| Час | h | 124 окружности | 15° | π12 рад |
| Минута | m | 11440 окружности, 160 часа |
14°, 15' | π720 рад |
| Секунда | s | 186400 окружности, 13600 часа, |
1240°, 14', 15'' | π43 200 рад |
- Точка весеннего равноденствия имеет прямое восхождение 0h;
- Точка летнего солнцестояния имеет прямое восхождение 6h;
- Точка осеннего равноденствия имеет прямое восхождение 12h;
- Точка зимнего солнцестояния имеет прямое восхождение 18h.
Звёздное время s, часовой угол светила t и его прямое восхождение α связаны:
В момент верхней кульминации часовой угол равняется нулю, следовательно, звёздное время равно прямому восхождению светил в верхней кульминации. Прямое восхождение точки весеннего равноденствия равно нулю, и её часовой угол всегда равен звёздному времени[1].
Прямое восхождение — астрономический эквивалент земной долготы во второй экваториальной системе. И прямое восхождение, и долгота измеряют угол «восток-запад» вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Начало отсчёта долготы на Земле — нулевой меридиан; начало отсчёта прямого восхождения на небе — точка весеннего равноденствия.
Прямое восхождение Солнца
Склонение и прямое восхождение Солнца меняются в течение года. В момент весеннего равноденствия прямое восхождение Солнца равно нулю, и оно постоянно увеличивается, пока снова не окажется в точке весеннего равноденствия и не обнулится. Однако, оно изменяется неравномерно: это вызвано тем, что орбита Земли не круговая, а эллиптическая, а также наклоном плоскости экватора к плоскости эклиптики. Это приводит к тому, что между верхними кульминациями Солнца проходит не в точности 24 часа, а чуть больше или меньше, и это затрудняет измерение времени по Солнцу. Отклонение истинного Солнца от среднего называется уравнением времени[1].
Влияние прецессии
Из-за прецессии оси Земли меняется положение полюсов мира и небесного экватора с периодом в 26000 лет. Следовательно, даже у неподвижных объектов меняется склонение и прямое восхождение. Поэтому для учёта прецессии астрономам нужно пересчитывать координаты на определённый момент времени, называемый эпохой. В данный момент используется эпоха J2000.0, которой соответствует момент 1 января 2000 в 12:00 TT. В 1976 году на ассамблее Международного Астрономического Союза было решено использовать эту эпоху с 1984 года; до этого по очереди использовались эпохи B1875.0, B1900.0 и B1950.0[2][3][4].
Примечания
- Кононович Э.В., Мороз В.И. Общий курс астрономии. — 2-е, исправленное. — УРСС, 2004. — С. 19—40. — 544 с. — ISBN 5-354-00866-2.
- Moulton (1918), pp. 92-95.
- Aoki, S.; Soma, M.; Kinoshita, H.; Inoue, K. Conversion matrix of epoch B 1950.0 FK 4-based positions of stars to epoch J 2000.0 positions in accordance with the new IAU resolutions (англ.) // Astronomy and Astrophysics : journal. — 1983. — December (vol. 128, no. 3). — P. 263—267. — ISSN 0004-6361. — .
Ссылки
- Merrifield, Michael (α,δ) – Right Ascension & Declination. Sixty Symbols. Brady Haran for the University of Nottingham.