Псевдоскалярное произведение

Псевдоскалярным[1] или косым произведением векторов $\mathbf {a}$ и $\mathbf {b}$ на плоскости называется число

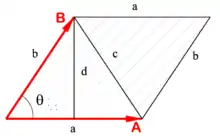
\mathbf {a} \wedge \mathbf {b} =|\mathbf {a} |\cdot |\mathbf {b} |\sin \theta ,

где $\theta =\angle (\mathbf {a} ,\mathbf {b} )$ — угол вращения (против часовой стрелки) от $\mathbf {a}$ к $\mathbf {b}$ . Если хотя бы один из векторов $\mathbf {a}$ и $\mathbf {b}$ нулевой, то полагают $\mathbf {a} \wedge \mathbf {b} =0$ . Геометрически псевдоскалярное произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора. С её помощью удобно работать с площадями многоугольников, выражать условия коллинеарности векторов и находить углы между ними.

Псевдоскалярное произведение существует только для 2-мерных векторов, его аналогом в трехмерном пространстве является тройное скалярное произведение.

Свойства

Линейность: $\mathbf {a} \wedge (\lambda \mathbf {b} +\mu \mathbf {c} )=\lambda \mathbf {a} \wedge \mathbf {b} +\mu \mathbf {a} \wedge \mathbf {c} .$ Здесь $\lambda$ , $\mu$ — произвольные вещественные числа.
Антикоммутативность: $\mathbf {a} \wedge \mathbf {b} =-\mathbf {b} \wedge \mathbf {a}$ .
$\mathbf {a} \wedge \mathbf {b}$ является псевдоскаляром, то есть инвариантом при всех невырожденных изометриях, не включающих отражений.
Псевдоскалярное произведение $\mathbf {a} \wedge \mathbf {b}$ $\text{[math]}$ — это ориентированная площадь параллелограмма, натянутого на векторы $\mathbf {a}$ $\text{[math]}$ и $\mathbf {b}$ $\text{[math]}$ .
- Абсолютная величина псевдоскалярного произведения $|\mathbf {a} \wedge \mathbf {b} |$ — это площадь такого параллелограмма.
- Ориентированная площадь треугольника $\triangle ABC$ выражается формулой
  $S(A,B,C)={\frac {1}{2}}({\overrightarrow {AB}}\wedge {\overrightarrow {AC}}),$
а его площадь, следовательно, равна модулю этой величины.
Если рассматривать плоскость в трёхмерном пространстве, то
$\mathbf {a} \wedge \mathbf {b} =\pm (\mathbf {a} \times \mathbf {b} )\cdot \mathbf {n} ,$

где «

\times

» и «

\ \cdot

» соответственно — векторное и скалярное произведение, а

\mathbf {n}

— единичный вектор нормали к плоскости. Знак плюс берется в случае, если правый базис на плоскости, дополненный вектором

\mathbf {n}

, образует также правый базис; в противном случае минус.

$\mathbf {a} \wedge \mathbf {b} =\mathbf {0}$ — необходимое и достаточное условие коллинеарности ненулевых векторов на плоскости. Нулевой вектор для удобства работы с более употребительным скалярным произведением обычно считают ортогональным любому другому вектору, хотя это является произвольным соглашением.
Из линейности и антикоммутативности следует, что если на плоскости задан ортонормированный базис $\langle \mathbf {e} _{1},\mathbf {e} _{2}\rangle ,~~\angle (\mathbf {e} _{1},\mathbf {e} _{2})={\tfrac {\pi }{2}},$ и два вектора, имеющих в нём координаты $\mathbf {a} =(a_{1},a_{2}),~~\mathbf {b} =(b_{1},b_{2}),$ то их псевдоскалярное произведение равно определителю

\mathbf {a} \wedge \mathbf {b} ={\begin{vmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{vmatrix}}

Это выражение также можно записать через символ Леви-Чивиты в двумерном пространстве:

\mathbf {a} \wedge \mathbf {b} =\sum _{i,\;j=1}^{2}\varepsilon _{ij}a^{i}b^{j}

См. также

Примечания

Прасолов В. В., Задачи по планиметрии. — 4-е изд., дополненное — М.: МЦНМО, 2001. — 584 с. ; ISBN 5-900916-82-0.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Прасолов В. В., Задачи по планиметрии. — 4-е изд., дополненное — М.: МЦНМО, 2001. — 584 с. ; ISBN 5-900916-82-0.