Символ Леви-Чивиты

Изображение символа Леви-Чивиты.

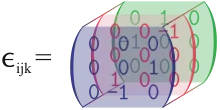
В трёхмерном пространстве, в правом ортонормированном базисе (или вообще в правом базисе с единичным определителем метрики) символ Леви-Чивиты определяется следующим образом:

${\displaystyle \varepsilon _{ijk}={\begin{cases}+1&P(i,j,k)=+1\\-1&P(i,j,k)=-1\\0&i=j\bigvee j=k\bigvee k=i\end{cases}}}$

то есть для чётной перестановки P(i, j, k) равен 1 (для троек (1,2,3), (2,3,1), (3,1,2)), для нечётной перестановки P(i, j, k) равен −1 (для троек (3,2,1), (1,3,2), (2,1,3)), а в остальных случаях равен нулю, при повторении. Для компонент ${\displaystyle \ \varepsilon _{ijk}}$ в левом базисе берутся противоположные числа.

Для общего случая (произвольных косоугольных координат с правой ориентацией базисных векторов) это определение обычно меняется на

${\displaystyle \varepsilon _{ijk}={\begin{cases}+{\sqrt {g}}&P(i,j,k)=+1\\-{\sqrt {g}}&P(i,j,k)=-1\\0&i=j\bigvee j=k\bigvee k=i\end{cases}}}$

где ${\displaystyle \ g}$ — определитель матрицы метрического тензора ${\displaystyle \ g_{ij}}$, представляющий квадрат объёма параллелепипеда, натянутого на базис. Для компонент ${\displaystyle \ \varepsilon _{ijk}}$ в левом базисе берутся противоположные числа.

Такой набор компонент ${\displaystyle \varepsilon _{ijk}}$ представляет собой (истинный) тензор. Если, как это иногда делается в литературе, в качестве определения ${\displaystyle \varepsilon _{ijk}}$ использовать приведённые выше формулы для любой — как правой, так и левой — системы координат, то получившийся набор чисел будет представлять псевдотензор.

При этом ${\displaystyle \varepsilon ^{ijk}}$ будет таким же, но с заменой ${\displaystyle \ {\sqrt {g}}}$ на ${\displaystyle \ 1/{\sqrt {g}}}$ .

${\displaystyle \varepsilon _{ijk}}$ может определяться также как смешанное произведение векторов базиса, в котором символ применяется:

${\displaystyle \varepsilon _{ijk}=\left[{\vec {e}}_{i}{\vec {e}}_{j}{\vec {e}}_{k}\right]}$.

Это определение для любого, правого или левого базиса, так как разница знака для левых и правых базисов заключена в смешанном произведении. Абсолютная величина каждой ненулевой компоненты равна объёму параллелепипеда, натянутого на базис ${\displaystyle \ \{{\vec {e_{i}}}\}}$. Тензор, как и положено, антисимметричен по любой паре индексов. Определение эквивалентно приведенным выше.

• Иногда пользуются альтернативным определением символа Леви-Чивиты без множителя ${\displaystyle {\sqrt {g}}\ }$ в любых базисах (то есть таким, что все его компоненты всегда равны ±1 или 0, как в нашем определении для ортонормированных базисов). В этом случае он сам по себе не является представлением тензора. Домноженный же на ${\displaystyle {\sqrt {g}}\ }$ объект (совпадающий с ${\displaystyle \varepsilon _{ijk}}$ в нашем определении и являющийся тензором) в этом случае обозначается другой буквой и называется, как правило, элементом объёма. Мы же здесь следуем определению Леви-Чивиты. (Это замечание имеет силу не только для трехмерного пространства, но и для любой размерности).

Как видно уже из определения через смешанное произведение, символ Леви-Чивиты связан с ориентированным объёмом и ориентированной площадью, представленной как вектор.

В трехмерном (евклидовом) пространстве смешанное произведение трех векторов

${\displaystyle V=\varepsilon _{ijk}a^{i}b^{j}c^{k}}$

— это ориентированный объём (псевдоскаляр, модуль которого равен объёму, а знак зависит от ориентации тройки векторов) параллелепипеда, натянутого на три вектора ${\displaystyle {\vec {a}}}$, ${\displaystyle {\vec {b}}}$ и ${\displaystyle {\vec {c}}}$

Векторное произведение двух векторов

${\displaystyle S_{i}=\varepsilon _{ijk}a^{j}b^{k}}$

— это ориентированная площадь параллелограмма, стороны которого — векторы ${\displaystyle {\vec {a}}}$ и ${\displaystyle {\vec {b}}}$, представленная псевдовектором, длина которого равна площади, а направление — ортогонально к плоскости параллелограмма.

Этот смысл сохраняется для любой размерности пространства n, если, конечно, брать ${\displaystyle \varepsilon }$ с соответствующим количеством индексов, под объёмом понимать n-мерный объём, а под площадью — (n−1)-мерную (гипер-)площадь. При этом, естественно, в соответствующую формулу входит n и (n−1) векторов — сомножителей. Например, для 4-мерного (евклидова) пространства:

${\displaystyle V=\varepsilon _{ijkm}a^{i}b^{j}c^{k}d^{m},}$

${\displaystyle S_{i}=\varepsilon _{ijkm}a^{j}b^{k}c^{m}.}$

• Определитель матрицы A размера 3×3 можно записать (здесь подразумевается стандартный, а следовательно ортонормированный базис):

  ${\displaystyle {\begin{vmatrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\\\end{vmatrix}}=\sum _{i,j,k=1}^{3}\varepsilon _{ijk}a_{i}b_{j}c_{k}.}$

• Векторное произведение двух пространственных векторов записывается через этот символ:

  ${\displaystyle {\vec {a}}\times {\vec {b}}=\sum _{i,j,k=1}^{3}\varepsilon _{ijk}{\vec {e}}^{\ i}a^{j}b^{k}={\vec {c}}}$, где ${\displaystyle c_{i}=\sum _{j,k=1}^{3}\varepsilon _{ijk}a^{j}b^{k}}$ — его компоненты, а ${\displaystyle \ {\vec {e}}^{\ i}}$ — векторы базиса.

• Смешанное произведение векторов тоже:

  ${\displaystyle \left[{\vec {a}}{\vec {b}}{\vec {c}}\right]=\sum _{i,j,k=1}^{3}\varepsilon _{ijk}a^{i}b^{j}c^{k}.}$

• В следующей формуле ${\displaystyle \delta }$ обозначает символ Кронекера:

  ${\displaystyle \varepsilon _{ijk}\varepsilon ^{lmn}={\begin{vmatrix}\delta _{i}^{l}&\delta _{i}^{m}&\delta _{i}^{n}\\\delta _{j}^{l}&\delta _{j}^{m}&\delta _{j}^{n}\\\delta _{k}^{l}&\delta _{k}^{m}&\delta _{k}^{n}\\\end{vmatrix}}.}$

• В случае суммирования по общему индексу

${\displaystyle \sum _{i=1}^{3}\varepsilon _{ijk}\varepsilon _{imn}=\delta _{jm}\delta _{kn}-\delta _{jn}\delta _{km}}$

• В случае двух общих индексов ${\displaystyle i,\;j}$, тензор сворачивается следующим образом:

${\displaystyle \sum _{i=1}^{3}\sum _{j=1}^{3}\varepsilon _{ijk}\varepsilon _{ijn}=2\delta _{kn}}$

(Везде здесь в случае ортонормированного базиса все индексы можно просто переписать как нижние.)

Символ Леви-Чивиты может быть легко обобщён на любое количество измерений больше единицы, если пользоваться определением через чётность перестановок индексов:

${\displaystyle \varepsilon _{ijk\ell \dots }=\left\{{\begin{matrix}~\\~\\~\end{matrix}}\right.}$	${\displaystyle +{\sqrt {g}},}$ если ${\displaystyle (i,j,k,\ell ,\dots )}$ есть чётная перестановка набора ${\displaystyle (1,2,3,4,\dots )\;;}$
	${\displaystyle -{\sqrt {g}},}$ если ${\displaystyle (i,j,k,\ell ,\dots )}$ есть нечётная перестановка набора ${\displaystyle (1,2,3,4,\dots )\;;}$
	${\displaystyle 0}$, если хотя бы два индекса совпадают.

То есть он равен знаку (signum) перестановки, умноженному на корень из определителя метрики ${\displaystyle {\sqrt {g}}={\sqrt {\det {\{g_{ij}\}}}}}$ в случае, когда индексы принимают значения, реализующие перестановку набора ${\displaystyle (1,2,3,\dots ,n)}$, а в остальных случаях ноль. (Как видим, количество индексов равно размерности пространства ${\displaystyle n}$.)

• В псевдоевклидовых пространствах в случае, если сигнатура метрики такова, что ${\displaystyle g<0}$, вместо него как правило берут ${\displaystyle -g}$, чтобы ${\displaystyle {\sqrt {g}}}$ получался вещественным.

• Во всех размерностях, где символ Леви-Чивиты определён, он представляет тензор (имеется в виду главным образом то, что надо проследить за тем, чтобы количество индексов символа совпадало с размерностью пространства). Кроме того, как видно из написанного выше, какие-то трудности с обычным определением символа Леви-Чивиты могут быть в пространствах, где не определён метрический тензор, или, скажем, ${\displaystyle \det {\{g_{ij}\}}=0}$ или ${\displaystyle \det {\{g^{ij}\}}=0}$.

Можно показать, что для ${\displaystyle n}$ измерений выполняются свойства, аналогичные трёхмерным:

• ${\displaystyle \sum _{i,j,k,\dots =1}^{n}\varepsilon _{ijk\dots }\varepsilon ^{ijk\dots }=n!}$

— что связано с тем, что существует ${\displaystyle n!}$ перестановок набора ${\displaystyle (1,2,3,\dots ,n)}$, а следовательно, столько же ненулевых компонент ${\displaystyle \varepsilon }$ с ${\displaystyle n}$ индексами.

• ${\displaystyle \varepsilon _{ijk\dots }\varepsilon ^{pqr\dots }={\begin{vmatrix}\delta _{i}^{p}&\delta _{i}^{q}&\delta _{i}^{r}&\dots \\\delta _{j}^{p}&\delta _{j}^{q}&\delta _{j}^{r}&\dots \\\delta _{k}^{p}&\delta _{k}^{q}&\delta _{k}^{r}&\dots \\\vdots &\vdots &\vdots &\ddots \\\end{vmatrix}}.}$

После раскрытия определителя появляется множитель ${\displaystyle n!}$ и производятся упрощения в соответствующих символах Кронекера.

• Псевдоскалярное произведение двух векторов в двумерном пространстве:

  ${\displaystyle {{\vec {a}}\vee {\vec {b}}}=\sum _{i,j=1}^{2}\varepsilon _{ij}a^{i}b^{j}}$

• Определитель матрицы ${\displaystyle A}$ размера ${\displaystyle n\times n}$ можно удобно записать с использованием ${\displaystyle n}$-мерного символа Леви-Чивиты

  ${\displaystyle \det {A}=\sum _{i,j,k,\ldots =1}^{n}\varepsilon _{ijk\ldots }A_{1i}A_{2j}A_{3k}\cdots =\sum _{i_{1},i_{2},i_{3},\ldots ,i_{n}=1}^{n}\varepsilon _{i_{1}i_{2}i_{3}\cdots i_{n}}A_{1i_{1}}A_{2i_{2}}A_{3i_{3}}\cdots A_{ni_{n}}}$

что является, по сути, просто переписанным с помощью этого символа определением определителя (одним из самых распространенных). Здесь базис подразумевается стандартным, и ненулевые компоненты ${\displaystyle \varepsilon _{ijk\ldots }}$ принимают тут значения ${\displaystyle \pm 1}$.

• прямое ${\displaystyle n}$-мерное обобщение векторного произведения ${\displaystyle n-1}$ штук ('${\displaystyle n}$-мерных) векторов:

${\displaystyle {\vec {p}}={{\vec {a}}\times {\vec {b}}\times {\vec {c}}\cdots }=\sum _{i,j,k,m,\ldots =1}^{n}\varepsilon _{ijkm\ldots }{\vec {f}}^{i}a^{j}b^{k}c^{m}\cdots }$,

где ${\displaystyle p_{i}=\sum _{j,k,m,\ldots =1}^{n}\varepsilon _{ijkm\ldots }a^{j}b^{k}c^{m}\cdots }$ — его компоненты, а ${\displaystyle {\vec {f}}^{\ i}}$ — базисные векторы. (Здесь для краткости записано выражение для ковариантных компонент и разложение в дуальном базисе).

• прямое ${\displaystyle n}$-мерное обобщение смешанного произведения ${\displaystyle n}$ штук (${\displaystyle n}$-мерных) векторов:

  ${\displaystyle \left[{\vec {a}}{\vec {b}}{\vec {c}}\cdots \right]=\sum _{i,j,k,\ldots =1}^{n}\varepsilon _{ijk\ldots }a^{i}b^{j}c^{k}\cdots }$

В безындексной тензорной записи символ Леви-Чивиты заменяется оператором дуальности, называемым звёздочка Ходжа, или просто оператор звездочка:

${\displaystyle (*\eta )_{i_{1},i_{2},\ldots ,i_{n-k}}={\frac {1}{k!}}\eta ^{j_{1},\ldots ,j_{k}}\varepsilon _{j_{1},\ldots ,j_{k},i_{1},\ldots ,i_{n-k}}}$

(для произвольного тензора ${\displaystyle \eta ,}$ учитывая эйнштейновское правило суммирования).

• Символ Кронекера
• Метрический тензор
• Символ Кристоффеля

• Hermann R. (ed.), Ricci and Levi-Civita’s tensor analysis papers, (1975) Math Sci Press, Brookline (определение символа — см. стр. 31).
• Charles W. Misner, Kip S. Thorne, John Archibald Wheeler, Gravitation, (1970) W.H. Freeman, New York; ISBN 0-7167-0344-0. (См. параграф 3.5 для обзора применения тензоров в общей теории относительности).
• Русский перевод: Ч. Мизнер, К. Торн, Дж. Уилер, Гравитация, (1977) Москва, «Мир» (См. по указателю — Леви-Чивиты тензор).
• Димитриенко Ю. И., Тензорное исчисление, М.:Высшая школа, 2001, 575 с.