L-система
L-система или система Линденмайера — это параллельная система переписывания и вид формальной грамматики. L-система состоит из алфавита символов, которые могут быть использованы для создания строк, набора порождающих правил, которые задают правила подстановки вместо каждого символа, начальной строки («аксиомы»), с которой начинается построение, и механизма перевода образованной строки в геометрические структуры. L-системы предложил и развивал в 1968 Аристид Линденмайер, венгерский биолог и ботаник из Утрехтского университета. Линденмайер использовал L-системы для описания поведения клеток растений и моделирования процесса развития растения. L-системы использовались также для моделирования морфологии различных организмов[1] и могут быть использованы для генерации самоподобных фракталов, таких как системы итерируемых функций.

Истоки

В качестве биолога Линденмайер работал с дрожжами и нитевидными грибами и изучал схемы роста различных видов водорослей, таких как синезелёные водоросли Anabaena catenula. Первоначально L-системы были разработаны для формального описания развития таких простых многоклеточных организмов и для иллюстрации связи между соседними клетками растения. Позже система была расширена для описания высших растений и сложных ветвящихся структур.
Структура L-системы
Рекурсивная природа правил L-системы приводит к самоподобию и потому подобные фракталам формы легко описываются с помощью L-системы. Модели растений и выглядящие естественно органические формы легко сформировать, так как при увеличении уровня рекурсии модель медленно «растёт» и становится более сложной. Системы Линденмайера популярны также в генерации искусственной жизни.
Грамматики L-систем очень похожи на полусистемы Туэ (см. «Иерархия Хомского»). L-системы теперь известны как параметрические L системы, которые определяются как кортеж
- G = (V, ω, P),
где
- V (алфавит) — это множество символов, содержащих как элементы, которые могут быть заменены (переменные), так и элементы, которые не могут быть заменены ("константы" или "терминальные символы")
- ω (старт, аксиома или инициатор) — это строка символов из V, определяющая начальное состояние системы
- P — это множество порождающих правил, определяющих, каким образом переменные могут быть заменены комбинациями констант и других переменных. Порождающее правило состоит из двух строк, прототип и преемник. Для любого символа A, входящего в алфавит V, не входящего в левую часть правил P, предполагается правило вывода A → A. Эти символы называются константами или терминальными символами. (см. «Закон тождества»).
Правила грамматики L-системы применяются итеративно, начиная с аксиомы (начального состояния). На итерации применяется как можно больше правил. Факт, что на каждой итерации применяется как можно больше правил, отделяет L-систему от формального языка генерируемого по формальной грамматике, которая применяет только одно правило на итерацию. Если бы правила вывода применялись по одному, легко было бы сгенерировать язык, а не L-систему. Таким образом, L-системы являются подмножеством языков.
L-система является контекстно-свободной, если каждое правило вывода ссылается только на индивидуальные символы, а не на их соседей. Контекстно-свободные L-системы определяются контекстно-свободной грамматикой. Если правило зависит не только от единичного символа, но и от соседних, система называется контекстно-зависимой L-системой.
Если существует в точности одно правило для каждого символа, говорят, что L-система детерминированная (детерминированная контекстно-независимая L-система называется D0L системой). Если имеется несколько правил и каждая выбирается с некоторой вероятностью на каждой итерации, то это стохастическая L-система.
Чтобы использовать L-системы для генерации графических образов, требуется, чтобы символы в модели относились к элементам рисунка на экране компьютера. Например, программа Fractint использует черепашью графику (похожую на графику в языке Лого) для получения изображения на экране. Программа интерпретирует каждую константу в модели L-системы как команды системы черепашьей графики.
Примеры L-систем
Пример 1: Водоросли
Оригинальная L-система Линденмайера для моделирования роста водорослей.
- переменные : A B
- константы : нет
- аксиома : A
- правила : (A → AB), (B → A)
Система даёт
- n = 0 : A
- n = 1 : AB
- n = 2 : ABA
- n = 3 : ABAAB
- n = 4 : ABAABABA
- n = 5 : ABAABABAABAAB
- n = 6 : ABAABABAABAABABAABABA
- n = 7 : ABAABABAABAABABAABABAABAABABAABAAB
Пример 1: Водоросли, объяснение
n=0: A старт (аксиома/инициатор)
/ \
n=1: A B начальная единственная A превращается в AB по правилу (A → AB), правило (B → A) не может быть применено
/| \
n=2: A B A к строке AB применяются все правила, A снова превращается в AB, а B превращается A
/| | |\
n=3: A B A A B заметьте, что все A переводятся в копию себя и добавляется B, которая превращается ...
/| | |\ |\ \
n=4: A B A A B A B A ... в A в следующем поколении, что приводит к рекурсии
Результатом будут слова Фибоначчи. Если посчитать длину каждой строки, получим знаменитую последовательность Фибоначчи (опуская первую 1):
- 1 2 3 5 8 13 21 34 55 89 ...
Для каждой строки, если мы отсчитаем k-ю позицию с левого конца строки, значение зависит от того, попадает ли k, умноженное на золотое сечение, в интервал . Отношение вхождений букв A к B также сходится к золотому сечению.
Этот пример даёт тот же результат (в смысле длины строк, не в смысле последовательности букв A и B), если правило (A → AB) заменить на (A → BA), но при этом получим зеркально отражённые строки.
Эта последовательность является катенантной, поскольку , где является n-м поколением.
Пример 2: Дерево Пифагора
- переменные: 0, 1
- константы: [, ]
- аксиома: 0
- правила: (1 → 11), (0 → 1[0]0)
Фигура строится рекурсивным применением правил вывода к аксиоме. Каждый символ входной строки проверяется в списке правил, чтобы определить, на что следует заменить символ. В этом примере «1» на входе превращается в «11» на выходе, а «[» не меняется. Применяя правила вывода к аксиоме «0», получим:
| аксиома: | 0 |
| 1-ая рекурсия: | 1[0]0 |
| 2-ая рекурсия: | 11[1[0]0]1[0]0 |
| 3-я рекурсия: | 1111[11[1[0]0]1[0]0]11[1[0]0]1[0]0 |
| … |
Мы видим, что строки быстро растут в длине и сложности. Строку можно нарисовать в виде рисунка с помощью черепашьей графики, где каждому символу соответствует графическая операция для черепахи. В данном примере черепахе могут быть даны следующие команды:
- 0: рисуем отрезок, кончающийся листом
- 1: рисуем отрезок
- [: кладем в стек положение и угол рисования, поворачиваем влево на 45 градусов
- ]: считываем из стека положение и угол, поворачиваем вправо на 45 градусов
«Положим в стек» и «выберем из стека» относится к LIFO-стеку (более подробная грамматика потребовала бы разделить на «положим в стек» и «повернём»). Когда интерпретатор встречает «[», текущее положение черепахи и угол движения сохраняются в стеке, когда же встречается «]», положение и угол восстанавливаются. Если несколько значений заносятся в стек, восстанавливается последнее занесённое значение. В литературе L-системы, использующие такой подход к ветвлению, называют «bracketed L-systems» (скобочные L-системы)[2].
Применяя эти графические правила к полученной ранее строке, мы имеем:
 Аксиома
Аксиома Первая рекурсия
Первая рекурсия Вторая рекурсия
Вторая рекурсия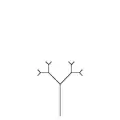 Третья рекурсия
Третья рекурсия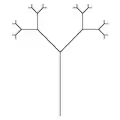 Четвёртая рекурсия
Четвёртая рекурсия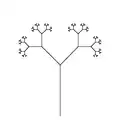 Седьмая рекурсия, уменьшенная в десять раз
Седьмая рекурсия, уменьшенная в десять раз
Пример 3: Множество Кантора

- переменные: A B
- константы: нет
- старт: A {стартовая строка}
- правила: (A → ABA), (B → BBB)
Пусть A означает «рисуем отрезок», а B означает «движемся».
Такая грамматика порождает знаменитое канторово фрактальное множество на вещественной оси R.
Пример 4: Кривая Коха
Вариант кривой Коха, использующей только прямые углы.
- переменные : F
- константы : + −
- старт : F
- правила : (F → F+F−F−F+F)
Здесь F означает «рисуем отрезок», + означает «повернуть влево на 90°», а − означает «повернуть вправо на 90°» (см. «Черепашья графика»).
- n = 0:
- F

- n = 1:
- F+F−F−F+F

- n = 2:
- F+F−F−F+F + F+F−F−F+F − F+F−F−F+F − F+F−F−F+F + F+F−F−F+F
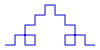
- n = 3:
- F+F−F−F+F+F+F−F−F+F−F+F−F−F+F−F+F−F−F+F+F+F−F−F+F +
- F+F−F−F+F+F+F−F−F+F−F+F−F−F+F−F+F−F−F+F+F+F−F−F+F −
- F+F−F−F+F+F+F−F−F+F−F+F−F−F+F−F+F−F−F+F+F+F−F−F+F −
- F+F−F−F+F+F+F−F−F+F−F+F−F−F+F−F+F−F−F+F+F+F−F−F+F +
- F+F−F−F+F+F+F−F−F+F−F+F−F−F+F−F+F−F−F+F+F+F−F−F+F

Пример 5: Треугольник Серпинского
Треугольник Серпинского, нарисованный с помощью L-системы.
- переменные: F G
- константы: + −
- старт: F−G−G
- правило: (F → F−G+F+G−F), (G → GG)
- угол: 120°
Здесь F и G означают «рисуем отрезок», + означает «повернуть вправо на угол», а − означает «повернуть влево на угол».
.png.webp) n = 2
n = 2.png.webp) n = 4
n = 4.png.webp) n = 6
n = 6
Можно также аппроксимировать треугольник Серпинского, используя L-систему создания стреловидной кривой Серпинского.
- переменные: A B
- константы: + −
- старт: A
- правила: (A → B−A−B), (B → A+B+A)
- угол: 60°
Здесь A и B означают «рисуем отрезок», + означает «повернуть влево на угол», а − означает «повернуть вправо на угол» (см. «Черепашья графика»).
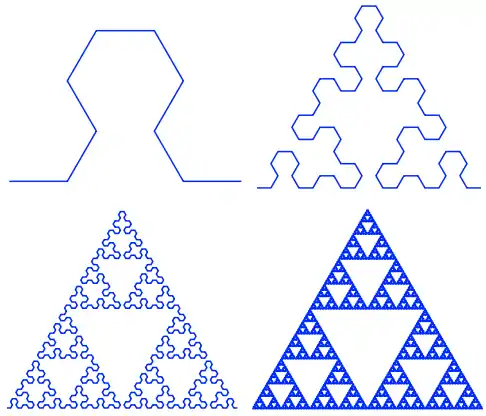
Пример 6: Кривая дракона
Кривая дракона, нарисованная с помощью L-системы.
- переменные : X Y
- константы : F + −
- старт : FX
- правила : (X → X+YF+), (Y → −FX−Y)
- угол : 90°
Здесь F означает «рисуем отрезок», − означает «повернуть влево на 90°», а + означает «повернуть вправо на 90°». X и Y не соответствуют какому-либо действию при рисовании, а используются только для построения кривой.
Пример 7: Фрактальное растение
- переменные : X F
- константы : + − [ ]
- старт : X
- правила : (X → F−[[X]+X]+F[+FX]−X), (F → FF)
- угол : 25°
Здесь F означает «рисуем отрезок», − означает «повернуть влево на 25°», а + означает «повернуть вправо на 25°». X не соответствует какому-либо действию при рисовании используется только для построения кривой. Квадратная скобка «[» соответствует сохранению текущих значений позиции и угла, которые восстанавливаются, когда выполняется соответствующий символ «]».

Варианты
Было сделано несколько разработок на основе техники L-систем, которые могут быть использованы совместно. Среди них cтохастические грамматики, контекстно-зависимые грамматики и параметрические грамматики.
Стохастические грамматики
Модели грамматик, которые мы сейчас рассматривали, являются детерминированными. То есть, если дан какой-либо символ из алфавита, имеется в точности одно правило, которое всегда выбирается и всегда выполняется одна и та же подстановка. Альтернативой является указание более одного правила вывода для символа, задав для каждого правила вероятность выполнения. Например, в грамматике примера 2 мы можем заменить правило переписывания «0» с
- 0 → 1[0]0
на вероятностное правило
- 0 (0.5) → 1[0]0
- 0 (0.5) → 0
При этих правилах вывода, когда встречается «0» во входной строке, с вероятностью 50 % поведение будет таким же, как и раньше, а с вероятностью 50 % ничего не меняется. Если используется стохастическая грамматика в контексте эволюции, рекомендуется инкорпорировать генератор случайности в генотип, так что стохастические свойства рисунка остаются постоянными между поколениями.
Контекстно-зависимые грамматики
Контекстно-зависимое правило вывода просматривает не только символы, которые он изменяет, но и символы предшествующие им и следующие за ними. Например, правило вывода:
- b < a > c → aa
преобразует "a" в "aa", но только если "a" окажется между "b" и "c" во входной строке:
- …bac…
Как и в случае случайного вывода, имеется несколько правил для обработки символы в различных контекстах. Если никакое порождающее правило не найдено для указанного контекста, предполагается тождественное преобразование, и символ не меняется. Если имеются как контекстно-независимые, так и зависимые правила вывода в той же грамматике, контекстно-зависимое правило вывода имеет преимущество (если его можно применить).
Параметрические грамматики
В параметрической грамматике каждый символ в алфавите имеет список параметров, ассоциированный с символом. Символ вместе с параметрами называется модулем и строка в параметрической грамматике — это последовательность модулей. Примером может служить следующая строка:
- a(0,1)[b(0,0)]a(1,2)
Параметры могут быть использованы как функцией рисования, так и правилами вывода. Правила вывода могут использовать параметры двумя путями. В первом случае параметр используется в условном выражении, определяющем, следует ли применять правило вывода. Во втором случае правило вывода может подменять фактические параметры. Например, правило вывода:
- a(x,y) : x == 0 → a(1, y+1)b(2,3)
Модуль a(x,y) испытывает преобразование по этому правилу, если выполняется x=0. Например, a(0,2) претерпит преобразование, а a(1,2) — нет.
На правой стороне правила вывода (в преемнике) могут быть подвергнуты преобразованию как параметры, так и целые модули. В примере выше модуль b(x,y) добавляется к строке с начальными параметрами (2,3). Параметры же уже существующего модуля преобразуются. При описанных выше правилах вывода,
- a(0,2)
Становится
- a(1,3)b(2,3)
так как параметр «x» модуля a(x,y) явно преобразуется в «1», а параметр «y» увеличивается на единицу.
Параметрические грамматики позволяют длину отрезка и угол ответвления задать в грамматике, а не в методах интерпретации черепашьей графики. Если возраст также задаётся параметром для модуля, правила могут быть изменены в зависимости от возраста сегмента растения, что позволяет создавать анимацию всего жизненного цикла дерева.
Другие категории L-систем
- D0L-системы = детерминированные контекстно-свободные системы (см. выше)
- Размножающиеся L-системы («Propagative L-systems», «pL-systems») — это системы, в которых хотя бы одно правило имеет в правой части (в выводе) по меньшей мере две буквы. Неразмножающиеся системы имеют в правой части только один символ. Длина слова в этом случае не меняется[3].
- Скобочные L-системы (см. Пример 2)
- 0L-системы, 1L-системы, 2L-системы (IL-системы, известные также как (k,l)-системы)[4].
- Табличные L-системы ( «T0L-системы») — это системы, работающие с несколькими наборами правил. Для выбора набора правил используется внешний механизм контроля. Табличные L-системы были введены и формализованы Розенбергом в 1975 для моделирования влияния среды на рост растений[5] .
Открытые проблемы
Имеется много открытых проблем, связанных с изучением L-систем. Например:
- Описание всех детерминированных контекстно-свободных локально катентативных L-систем. (Полное решение известно только для случая трёх переменных) [6].
- Если задана структура, найти L-систему, которая может воспроизвести эту структуру.
- Если даны две pL-системы и функция интерполяции, будут ли результирующие рисунки конгруэнтны [4]?
- Если дана pL-система и функция интерпретации, будет ли результирующая кривая замкнутой? Будет ли она самопересекающейся или древовидной? Будут ли некоторые отрезки нарисованы более одного раза?[4]?
Ответы на эти вопросы интересны не только с теоретической точки зрения, они полезны также при построении pL-систем для создания рисунков с заданными свойствами[4].
Типы L-систем
L-системы на вещественной оси R:
Общеизвестные L-системы на плоскости R2:
- Заполняющие пространство кривые (Кривая Гильберта, Кривая Пеано, Церковь Декинга, Колам),
- медианные заполняющие пространство кривые (Кривая Леви, Дракон Хартера — Хейтуэя, Дракон Дэвиса-Кнута),
- мозаики (Мозаика «Сфинкс», Мозаика Пенроуза),
- деревья, растения, и тому подобное.
См. также
- Цифровой морфогенез
- Фрактал
- Система итерируемых функций
- Кривая Гильберта
- Стохастическая контекстно-свободная грамматика
- SpeedTree
Примечания
- Rozenberg, Salomaa, 1980.
- Manousakis, 2006, с. 26.
- Manousakis, 2006, с. 28.
- Prusinkiewicz, 1986, с. 252.
- Manousakis, 2006, с. 29.
- Kari, Rozenberg, Salomaa, 1997, с. 262.
Литература
- Grzegorz Rozenberg, Arto Salomaa. The mathematical theory of L systems. — New York: Academic Press, 1980. — ISBN 0-12-597140-0.
- Przemysław Prusinkiewicz, Aristid Lindenmayer. The Algorithmic Beauty of Plants. — Springer, 2004.
- Grzegorz Rozenberg, Arto Salomaa. Lindenmayer Systems: Impacts on Theoretical Computer Science, Computer Graphics, and Developmental Biology. — Springer-Verlag,, 1992. — ISBN 978-3-540-55320-5.
- D.S. Ebert, F.K. Musgrave, D. Peachey, K. Perlin. Texturing and Modeling: A Procedural Approach. — Academic Press, 1994. — ISBN 0-12-228730-4.
- Burry, Jane, Burry Mark. The New Mathematics of Architecture. — New York: Thames and Hudson, 2010.
- Aristid Lindenmayer. Mathematical models for cellular interaction in development // J. Theoret. Biology. — 1968. — Вып. 18. — С. 280—315.
- P. Prusinkiewicz. Proceedings of Graphics Interface '86 / Vision Interface '86. — 1986. — С. 247−253..
- Handbook of Formal Languages / G.Rozenberg, A.Salomaa. — Springer, 1997. — Т. 1(Word, Language, Grammar). — С. 253-328. — ISBN 978-3-642-63863-3.
- Stelios Manousakis. Musical L-Systems. — The Hague: The Royal Conservatory, 2006. — (Master’s Thesis – Sonology).
Ссылки
- Algorithmic Botany at the University of Calgary
- Branching: L-system Tree Java-апплет и исходный код (открытый код) моделирования роста ботанических деревьев с использованием L-системы.
- Fractint L-System True Fractals
- "powerPlant", система моделирования ландшафта (с открытым кодом)
- Fractint home page
- Простой генератор L-систем (Windows)
- Lyndyhop: другой Простой генератор L-систем (Windows & Mac)
- An evolutionary L-systems generator (anyos*)
- eXtended L-Systems (XL), Relational Growth Grammars, программная система с открытым кодом, GroIMP.
- Java-апплет с множеством фрактальных рисунков, сгенерированных L-системами. Архивная копия от 6 августа 2016 на Wayback Machine
- My Graphics – приложение для iPhone/iPad, генерирующее некоторые рисунки на основе L-систем.
- Онлайновое экспериментирование с L-системами, используя JSXGraph (JavaScript)
- Flea Имплементация на языке Ruby LSYSTEM
- Lindenmayer power Генератор растений и фракталов на основе L-систем (JavaScript)
- Rozenberg, G. & Salomaa, A. (2001), L-systems, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Laurens Lapré's L-Parser Архивная копия от 13 сентября 2013 на Wayback Machine
- HTML5 L-Systems – эксперименты онлайн
- The vector-graphics program Использующий Inkscape парсер L-системы
- Сложност L-системы (недоступная ссылка)
- Имплементация парсера L-системы и простая черепашья графика на языке программирования Icon
- Генератор систем Линденмайера от Нолана Каррола
- Bloogen: L-Systems


