Неравенство о среднем арифметическом, геометрическом и гармоническом

Рис. 1

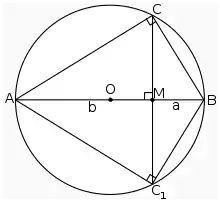
Количество доказательств этого неравенства на данный момент сравнимо, наверное, только с количеством доказательств теоремы Пифагора. Приведем красивое геометрическое доказательство для случая ${\displaystyle n=2}$. Пускай нам даны два отрезка длины ${\displaystyle a}$ и ${\displaystyle b}$. Тогда построим окружность диаметром ${\displaystyle a+b}$ (см. рис. 1). От одного из концов диаметра отметим точку ${\displaystyle M}$ на расстоянии ${\displaystyle a}$. Проведем через эту точку перпендикуляр к диаметру; полученная прямая пересечет окружность в двух точках, ${\displaystyle C}$ и ${\displaystyle C_{1}}$. Рассмотрим полученную хорду. Треугольник ${\displaystyle ABC}$ прямоугольный, так как угол ${\displaystyle C}$ — вписанный в окружность и опирающийся на её диаметр, а значит, прямой. Итак, ${\displaystyle CM}$ — высота треугольника ${\displaystyle ABC}$, а высота в прямоугольном треугольнике есть среднее геометрическое двух сегментов гипотенузы. Значит, ${\displaystyle CM={\sqrt {ab}}}$. Аналогично, из треугольника ${\displaystyle ABC_{1}}$ получаем, что ${\displaystyle C_{1}M={\sqrt {ab}}}$, поэтому ${\displaystyle CC_{1}=2CM=2C_{1}M=2{\sqrt {ab}}}$. Так как ${\displaystyle CC_{1}}$ — хорда окружности с диаметром ${\displaystyle a+b}$, а хорда не превосходит диаметра, то получаем, что ${\displaystyle 2{\sqrt {ab}}\leqslant a+b}$, или же ${\displaystyle {\sqrt {ab}}\leqslant {\frac {a+b}{2}}}$. Заметим, что равенство будет тогда, когда хорда будет совпадать с диаметром, то есть при ${\displaystyle a=b}$.

Алгебраическое же доказательство может быть построено следующим образом:

${\displaystyle {\frac {a+b}{2}}\geqslant {\sqrt {ab}}\;\Leftrightarrow \;(a+b)^{2}\geqslant 4ab\;\Leftrightarrow \;(a-b)^{2}\geqslant 0}$

Отметим, что первый переход равносилен в силу неотрицательности ${\displaystyle a}$ и ${\displaystyle b}$.

Достаточно положить ${\displaystyle \alpha ={\frac {a_{1}+a_{2}}{2}},\;\beta ={\frac {a_{3}+a_{4}}{2}}}$, а также ${\displaystyle \alpha '={\sqrt {a_{1}a_{2}}},\;\beta '={\sqrt {a_{3}a_{4}}}}$. Нетрудно видеть, в силу доказанного, что

${\displaystyle {\frac {\alpha +\beta }{2}}\geqslant {\sqrt {\alpha \beta }}\geqslant {\sqrt {\alpha '\beta '}}\;\Leftrightarrow \;{\frac {a_{1}+a_{2}+a_{3}+a_{4}}{4}}\geqslant {\sqrt[{4}]{a_{1}a_{2}a_{3}a_{4}}}}$.

Очевидно, переход от 2 к 4 по индукции влечёт за собой справедливость неравенства для ${\displaystyle N=2^{k}}$, причём для интересующего нас ${\displaystyle n}$ найдётся ${\displaystyle k:N\geqslant n}$. Полагая неравенство верным для ${\displaystyle N}$, докажем его справедливость для ${\displaystyle N-1}$. Для этого достаточно положить ${\displaystyle a_{N}={\sqrt[{N-1}]{a_{1}\cdot \ldots \cdot a_{N-1}}}}$, тогда

${\displaystyle {\frac {a_{1}+\ldots +a_{N}}{N}}\geqslant {\sqrt[{N}]{a_{1}\cdot \ldots \cdot a_{N}}}\;\Leftrightarrow \;}$${\displaystyle {\frac {a_{1}+\ldots +a_{N-1}+{\sqrt[{N-1}]{a_{1}\cdot \ldots \cdot a_{N-1}}}}{N}}\geqslant {\sqrt[{N}]{a_{1}\cdot \ldots \cdot a_{N-1}{\sqrt[{N-1}]{a_{1}\cdot \ldots \cdot a_{N-1}}}}}\;\Leftrightarrow \;}$${\displaystyle a_{1}+\ldots +a_{N-1}\geqslant (N-1){\sqrt[{N-1}]{a_{1}\cdot \ldots \cdot a_{N-1}}}\;\Leftrightarrow \;}$${\displaystyle {\frac {a_{1}+\ldots +a_{N-1}}{N-1}}\geqslant {\sqrt[{N-1}]{a_{1}\cdot \ldots \cdot a_{N-1}}}}$

По принципу индукции приведённое доказательство верно также и для ${\displaystyle n}$.

${\displaystyle {\sqrt[{n}]{x_{1}x_{2}...x_{n}}}\leqslant {\frac {x_{1}+x_{2}+...+x_{n}}{n}}}$

Поделим обе части неравенства на ${\displaystyle {\sqrt[{n}]{x_{1}x_{2}...x_{n}}}}$ и произведем замену ${\displaystyle y_{i}={\frac {x_{i}}{\sqrt[{n}]{x_{1}x_{2}...x_{n}}}}}$. Тогда при условиях ${\displaystyle y_{1}>0,y_{2}>0,...,y_{n}>0;\quad y_{1}y_{2}...y_{n}=1}$ необходимо доказать, что ${\displaystyle 1\leqslant {\frac {y_{1}+y_{2}+...+y_{n}}{n}}}$(1).

Воспользуемся методом математической индукции.

Нужно доказать, что если ${\displaystyle m_{1}>0,m_{2}>0,...,m_{n+1}>0;\quad m_{1}m_{2}...m_{n+1}=1}$, то ${\displaystyle m_{1}+m_{2}+...+m_{n+1}\geq n+1}$. Воспользуемся неравенством (1), которое по предположению индукции считаем доказанным для ${\displaystyle n}$. Пусть ${\displaystyle y_{1}=m_{1},y_{2}=m_{2},...,y_{n}=m_{n}m_{n+1}}$. Тогда выполнены оба условия ${\displaystyle y_{1}>0,y_{2}>0,...,y_{n}>0;\quad y_{1}y_{2}...y_{n}=1}$ и предполагается доказанным неравенство ${\displaystyle y_{1}+y_{2}+...+y_{n}\geq n}$ или ${\displaystyle m_{1}+m_{2}+...+m_{n}m_{n+1}\geq n}$. Теперь заменим ${\displaystyle m_{n}m_{n+1}}$ на ${\displaystyle m_{n}+m_{n+1}}$. Это возможно сделать в силу того, что ${\displaystyle m_{n}+m_{n+1}\geq m_{n}m_{n+1}+1}$ или ${\displaystyle m_{n}+m_{n+1}-m_{n}m_{n+1}-1\geq 0}$, что, очевидно выполняется, так как ${\displaystyle m_{n}(1-m_{n+1})-(1-m_{n+1})=(m_{n}-1)(1-m_{n+1})\geq 0}$. Таким образом, неравенство доказано.