Группа кватернионов

В теории групп группа кватернионов — это неабелева группа восьмого порядка, изоморфная набору из восьми кватернионов с операцией умножения. Она часто обозначается буквой Q или Q₈, и определяется заданием группы

Q=\langle -1,i,j,k\mid (-1)^{2}=1,\;i^{2}=j^{2}=k^{2}=ijk=-1\rangle ,

Диаграмма циклов группы Q. Каждый цвет отражает последовательность степеней некоторого элемента. Например, красный цикл отражает тот факт, что i ² = −1, i ³ = −i и i ⁴ = 1, а также (−i )² = −1, (−i )³ = i и (−i )⁴ = 1.

где 1 — единичный элемент, а элемент −1 коммутирует с остальными элементами группы.

Граф Кэли

Группа Q₈ имеет тот же порядок, что и диэдрическая группа D₄, но имеет другую структуру, что можно видеть на графах Кэли и диаграммах циклов:

Граф Кэли		Граф циклов
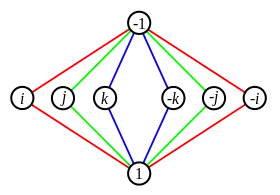
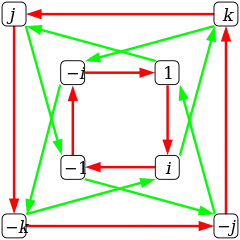Q₈ Красные стрелки обозначают умножение справа на i, а зелёные — умножение справа на j.	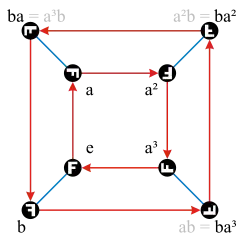D₄ Диэдрическая группа	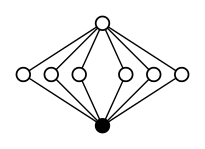Q₈	Dih₄

Диэдрическая группа D₄ получается из сплит-кватернионов таким же образом, что и Q₈ из кватернионов.

Таблица Кэли

Таблица Кэли (таблица умножения) для Q[1]:

Q×Q	1	−1	i	−i	j	−j	k	−k
1	1	−1	i	−i	j	−j	k	−k
−1	−1	1	−i	i	−j	j	−k	k
i	i	−i	−1	1	k	−k	−j	j
−i	−i	i	1	−1	−k	k	j	−j
j	j	−j	−k	k	−1	1	i	−i
−j	−j	j	k	−k	1	−1	−i	i
k	k	−k	j	−j	−i	i	−1	1
−k	−k	k	−j	j	i	−i	1	−1

Умножение шести мнимых единиц {±i, ±j, ±k} действует как векторное произведение единичных векторов в трёхмерном евклидовом пространстве.

{\begin{alignedat}{2}ij&=k,&ji&=-k,\\jk&=i,&kj&=-i,\\ki&=j,&ik&=-j.\end{alignedat}}

Свойства

Группа кватернионов имеет необычное свойство гамильтоновости — любая подгруппа группы Q является нормальной подгруппой, и при этом сама группа не является абелевой.[2] Любая гамильтонова группа содержит копию группы Q.[3]

Можно построить четырёхмерное векторное пространство с базисом {1, i, j, k} и превратить его в ассоциативную алгебру с использованием приведённой выше таблицы умножения базисных векторов и продолжив операцию умножения по дистрибутивности. Полученная алгебра будет телом кватернионов. Заметим, что это не то же самое, что и групповая алгебра Q (которая имеет размерность 8). Обратно, можно начать с кватернионов и определить группу кватернионов как мультипликативную подгруппу, состоящую из восьми элементов {1, −1, i, −i, j, −j, k, −k}. Комплексное четырёхмерное векторное пространство с тем же базисом называется алгеброй бикватернионов.

Заметим, что i, j и k имеют порядок 4 в Q и любые два из них порождают всю группу. Другое задание группы Q[4], показывающее это:

\langle x,y\mid x^{4}=1,x^{2}=y^{2},y^{-1}xy=x^{-1}\rangle .

Можно, например, взять i = x, j = y и k = xy.

Центром и коммутантом группы Q является подгруппа {±1}. Факторгруппа Q/{±1} изоморфна четверной группе Клейна V. Группа внутренних автоморфизмов группы Q изоморфна факторгруппе Q по центру, и потому также изоморфна четверной группе Клейна. Полная группа автоморфизмов группы Q изоморфна S₄, симметрической группе четырёх букв. Группой внешних автоморфизмов группы Q является S₄/V, которая изоморфна S₃.

Матричное представление

Группа кватернионов как подгруппа SL(2,C)

Группа кватернионов может быть представлена как подгруппа полной линейной группы GL₂(C). Представление

Q=\{\pm 1,\pm i,\pm j,\pm k\}\to \mathrm {GL} _{2}(\mathbf {C} )

определяется матрицами[5]

1\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}

i\mapsto {\begin{pmatrix}i&0\\0&-i\end{pmatrix}}

j\mapsto {\begin{pmatrix}0&1\\-1&0\end{pmatrix}}

k\mapsto {\begin{pmatrix}0&i\\i&0\end{pmatrix}}

Поскольку все из приведённых выше матриц имеют единичные определители, они задают представление группы Q в специальной линейной группе SL₂(C).

Группа кватернионов как подгруппа SL(2,3)

Существует также важное действие группы Q на восьми ненулевых элементах двумерного векторного пространства над конечным полем F₃. Представление

Q=\{\pm 1,\pm i,\pm j,\pm k\}\to \mathrm {GL} (2,3)

определяется матрицами

1\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}

i\mapsto {\begin{pmatrix}1&1\\1&-1\end{pmatrix}}

j\mapsto {\begin{pmatrix}-1&1\\1&1\end{pmatrix}}

k\mapsto {\begin{pmatrix}0&-1\\1&0\end{pmatrix}}

где {−1,0,1} — три элемента поля F₃. Поскольку определитель всех матриц над полем F₃ равен единице, это является представлением группы Q в специальной линейной группе SL(2, 3). Более того, группа SL(2, 3) имеет порядок 24, а Q является нормальной подгруппой группы SL(2, 3) с индекса 3.

Группа Галуа

Как показал Ричард Дин (Richard Dean) в 1981 году, группа кватернионов может быть задана как группа Галуа Gal(T/Q), где Q является полем рациональных чисел, а T является полем разложения многочлена

x^{8}-72x^{6}+180x^{4}-144x^{2}+36

над Q.

Доказательство использует основную теорему теории Галуа, а также две теоремы о циклических расширениях степени 4.[6]

Обобщённая группа кватернионов

Группа называется обобщённой группой кватернионов (или дициклической группой), если она имеет задание [4]

\langle x,y\mid x^{2n}=y^{4}=1,x^{n}=y^{2},y^{-1}xy=x^{-1}\rangle .

для некоторого целого n ≥ 2. Эта группа обозначается как Q_4n и имеет порядок 4n.[7] Коксетер обозначил эти дициклические группы как <2,2,n>, рассматривая их как частный случай бинарной полиэдральной группы <l,m,n>, связанной с полиэдральными группами (p,q,r) и диэдральной группой (2,2,n). Обычная кватернионная группа соответствует случаю n = 2. Обобщённая кватернионная группа изоморфна подгруппе группы GL₂(C), порождённой элементами

\left({\begin{array}{cc}\omega _{n}&0\\0&{\overline {\omega }}_{n}\end{array}}\right)

и

\left({\begin{array}{cc}0&-1\\1&0\end{array}}\right)

где ω_n = e^iπ/n[4]. Она также изоморфна группе, порождённой [8] кватернионами x = e^iπ/n и y = j.

Теорема Брауэра — Сузуки утверждает, что группы, для которых силовские 2-подгруппы являются обобщёнными кватернионами, не могут быть простыми.

См. также

Примечания

См. также a table таблицу на сайте Wolfram Alpha
См. книгу Холла (1999), p. 190
Курош А.Г. Теория групп. — М.: Наука, 1967. — С. 57.
Johnson, 1980, с. 44-45.
Artin, 1991.
Dean, Richard (1981). "A Rational Polynomial whose Group is the Quaternions". The American Mathematical Monthly 88 (1): 42–45. .
Некоторые авторы (например, Rotman, 1995, pp. 87, 351) называют эту группу дициклической группой, оставляя название обобщённая группа кватернионов для случая, когда n является степенью двойки.
Brown, 1982, с. 98.

Литература

Michael Artin. Algebra. — Prentice Hall, 1991. — ISBN 978-0-13-004763-2.
Kenneth S. Brown. Cohomology of groups. — Springer-Verlag, 1982. — ISBN 978-0-387-90688-1.
Henri Cartan, Samuel Eilenberg. Homological Algebra. — Princeton University Press, 1999. — ISBN 978-0-691-04991-5.
Richard A. Dean. A rational polynomial whose group is the quaternions // American Mathematical Monthly. — 1981. — С. 88:42–5.
D. Gorenstein. Finite Groups. — New York: Chelsea, 1980. — ISBN 978-0-8284-0301-6.
David L. Johnson. Topics in the theory of group presentations. — Cambridge University Press, 1980. — ISBN 978-0-521-23108-4.
Joseph J. Rotman. An introduction to the theory of groups. — 4. — Springer-Verlag, 1995. — ISBN 978-0-387-94285-8.
P.R. Girard. The quaternion group and modern physics // European Journal of Physics. — 1984. — С. 5:25–32.
Marshall Hall. The theory of groups. — 2. — AMS Bookstore, 1999. — ISBN 0-8218-1967-4.
Alexander G. Kurosh. Theory of Groups. — AMS Bookstore, 1979. — ISBN 0-8284-0107-1.

Внешние ссылки

Weisstein, Eric W. Quaternion group (англ.) на сайте Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] См. также a table таблицу на сайте Wolfram Alpha

[2] См. книгу Холла (1999), p. 190

[3] Курош А.Г. Теория групп. — М.: Наука, 1967. — С. 57.

[_47ec204143969536-4] Johnson, 1980, с. 44-45.

[_df28794fd8219b59-5] Artin, 1991.

[6] Dean, Richard (1981). "A Rational Polynomial whose Group is the Quaternions". The American Mathematical Monthly 88 (1): 42–45. .

[7] Некоторые авторы (например, Rotman, 1995, pp. 87, 351) называют эту группу дициклической группой, оставляя название обобщённая группа кватернионов для случая, когда n является степенью двойки.

[_3140690286b9435c-8] Brown, 1982, с. 98.