Группа Григорчука
Группа Григорчука — первый пример конечнопорождённой группы промежуточного роста (то есть её рост быстрее полиномиального, но медленнее экспоненциального).
Пример построен Григорчуком, промежуточный рост доказан им в работе 1984 года[1][2]. Тем самым был дан ответ на вопрос Милнора, заданный в 1968 году[3].
Построение
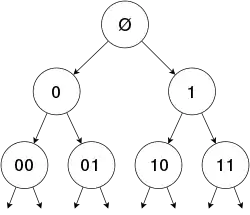
Группа строится через своё действие на бесконечном полном двоичном дереве.
Бесконечное полное двоичное дерево
Рассмотрим бесконечное полное двоичное корневое дерево Т2 и его автоморфизмы. Это дерево изоморфно любому своему поддереву, поэтому любой его автоморфизм может быть применён и к любому поддереву.
Каждая вершина дерева Т2 может быть помечена элементом множества Σ* всех конечных строк в алфавите Σ = {0,1}, включая пустую строку Ø. Пустая строка Ø соответствует корневой вершине Т2. Метка левого потомка каждого узла получается добавлением 0, правого — 1.
Любой автоморфизм дерева T2 сохраняет путь от корневого узла до любого другого и не перемещает ни один узел с одного уровня на другой. Выполнение этих свойств достаточно, чтобы перестановка множества вершин дерева была автоморфизмом дерева. Поэтому группа всех автоморфизмов Aut(Т2) соответствует группе всех таких перестановок σ множества строк Σ*, которые сохраняют длину строки (то есть длина x должна равняться длине σ(х)) и сохраняют отношение «начальный сегмент строки» (то есть если строка х является начальным сегментом строки y, то σ(х) является начальным сегментом σ(y)).
Образующие
Группа Григорчука G определяется как подгруппа группы Aut(Т2), порождённая определёнными четырьмя элементами а, b, с, d, то есть .
С точки зрения преобразования строк, состоящих из 0 и 1, автоморфизмы а, b, с, d определяются рекурсивно следующим образом:
- a(0x) = 1x, a(1x) = 0x;
- b(0x) = 0a(x), b(1x) = 1c(x);
- c(0x) = 0a(x), c(1x) = 1d(x);
- d(0x) = 0x, d(1x) = 1b(x)
для каждого x в Σ*. Например:
- a(11101) = 01101
- b(11101) = 1c(1101) = 11d(101) = 111b(01) = 1110a(1) = 11100
- c(11101) = 1d(1101) = 11b(101) = 111c(01) = 1110a(1) = 11100
- d(11101) = 1b(1101) = 11c(101) = 111d(01) = 11101

С точки зрения преобразования двоичного дерева элемент a меняет местами левое и правое поддеревья того дерева, на которое он действует. Остальные элементы действуют отдельно на каждое из этих двух поддеревьев, эти элементы могут быть рекурсивно представлены парами (два элемента пары соответствуют действию на левое и правое поддеревья):
- b = (a,c),
- c = (a,d),
- d = (1,b).
Здесь b = (a, c) означает, что b не меняет корень Т2, действует на левое поддерево как a, а на правое — как c. Здесь 1 обозначает тождественное отображение.
В не рекурсивном представлении действие элементов b, c, d выглядит так: начиная от корня, продвигаемся вниз, выбирая на каждом шаге правого потомка; при этом всякий раз к левому поддереву применяется операция a (меняющая местами два его поддерева), кроме каждого третьего шага, начиная с третьего, второго и первого шага для b, c и d, соответственно[4].
Свойства образующих
Ниже приведены основные следствия из этого построения[5].
- Каждый из элементов a, b, c, d имеет порядок 2 в G.
- Элементы b, c, d попарно коммутируют, и bc = cb = d, bd = db = c, dc = dc = b.
- В частности, — абелева группа порядка 4; она изоморфна прямому произведению двух циклических групп порядка 2.
- Группа G порождается a и любыми двумя из трёх элементов b, c, d (например, ).
- В приведённых выше рекурсивных обозначениях .
- Стабилизатор StG[1] в G — это подгруппа, порождённая b, c, d, aba, aca, ada. Подгруппа StG[1] является нормальной подгруппой индекса 2 в G, и
- G = StG[1] a StG[1].
- Каждый элемент G может быть записан как (положительное) слово из букв a, b, c, d без подслов формы aa, bb, cc, dd, cd, dc, bc, cb, bd, db.
- Такие слова называются сокращёнными.
- «Положительное слово» здесь означает, что в соответствующей записи отсутствуют элементы a−1, b−1 и т. д. Поскольку у всех этих образующих порядок равен 2, т. е. они сами себе обратны, то это необременительное условие.
- Сокращённое слово представляет собой элемент из стабилизатора StG[1] тогда и только тогда, когда это слово включает в себя чётное число вхождений a.
- Если w — сокращённое слово чётной длины с положительным чётным числом появлений a, то есть некоторые слова u, v, записанные через a, b, c, d (не обязательно сокращённые), такие, что в G есть w = (u, v) и |u| ≤ |w|/2, |v| ≤ |w|/2.
- Если w — сокращённое слово нечётной длины с положительным чётным числом вхождений a, то подобное утверждение тоже верно, но неравенства принимают вид: |u| ≤ (|w| + 1)/2, |v| ≤ (|w| + 1)/2.
Последнее свойство играет ключевую роль во многих доказательствах, поскольку оно позволяет использовать индукцию по длине слова.
Свойства
- Группа G бесконечна.[2]
- Группа G является остаточно конечной.[2]
- Группа G является 2-группой, то есть каждый элемент в G имеет конечный порядок, который равен степени 2.[1]
- Группа G имеет промежуточный рост.[2]
- В частности, группа G аменабельна.[2]
- Григорчук доказал, что рост группы G, , заключён между и .
- Позже было найдено точное значение показателя степени в показателе экспоненты в : , где — действительный корень многочлена [6].
- Каждая факторгруппа G по нетривиальной нормальной группе конечна.
- Каждая конечно порождённая подгруппа замкнута в про-конечной топологии на G.[7]
- Каждая максимальная подгруппа в G имеет конечный индекс.[8]
- Группа G конечно порождённая, но не конечно заданная.[2][9]
- Централизатор элемента конечно порожден тогда и только тогда, когда элемент сопряжен с порождающим элементом "а" [10]
- Индексы членов нижнего центрального ряда ограничены сверху числом 4 [11]
- Найдены примеры максимальных локально конечных подгрупп, они оказались бесконечными [12]
References
- Р. И. Григорчук, “К проблеме Бернсайда о периодических группах”, Функц. анализ и его прил., 14:1 (1980), 53—54
- Р. И. Григорчук, “Степени роста конечно-порожденных групп и теория инвариантных средних”, Изв. АН СССР. Сер. матем., 48:5 (1984), 939—985
- John Milnor, Problem No. 5603, American Mathematical Monthly, vol. 75 (1968), pp. 685—686.
- Rostislav Grigorchuk, Igor Pak. Groups of intermediate growth: an introduction : [англ.] // L'Enseignement Mathématique. — 2008. — Vol. 54. — P. 251-272. — arXiv:math/0607384. — doi:10.5169/seals-109938.
- Pierre de la Harpe. Topics in geometric group theory. Chicago Lectures in Mathematics. University of Chicago Press, Chicago. ISBN 0-226-31719-6; Ch. VIII, The first Grigorchuk group, pp. 211–264.
- Anna Erschler & Tianyi Zheng. Growth of periodic Grigorchuk groups // Inventiones mathematicae. — 2020. — Vol. 219. — P. 1069–1155. — doi:10.1007/s00222-019-00922-0.
- R. I. Grigorchuk, and J. S. Wilson. A structural property concerning abstract commensurability of subgroups. Journal of the London Mathematical Society (2), vol. 68 (2003), no. 3, pp. 671–682.
- Е. Л. Первова. Всюду плотные подгруппы одной группы автоморфизмов дерева // Тр. МИАН. — 2000. — Т. 231. — С. 356—367.
- И. Г. Лысëнок, “Система определяющих соотношений для группы Григорчука”, Матем. заметки, 38:4 (1985), 503—516
- А.В. Рожков. Централизаторы элементов в одной группе автоморфизмов деревьев // Изв. РАН. Сер. мат.. — 1993. — Т. 57, № 6. — С. 82-105.
- А.В. Рожков. Нижний центральный ряд одной группы автоморфизмов дерева // Мат. заметки.. — 1996. — Т. 60, № 2. — С. 225-237.
- А. В. Рожков. Максимальные локально конечные подгруппы в группе Григорчука // Мат. заметки.. — 1998. — Т. 63, № 4. — С. 617–624.