Эллиптическая система координат
Эллиптические координаты — двумерная ортогональная система координат, в которой координатными линиями являются конфокальные эллипсы и гиперболы. За два фокуса и обычно берутся точки и на оси декартовой системы координат.
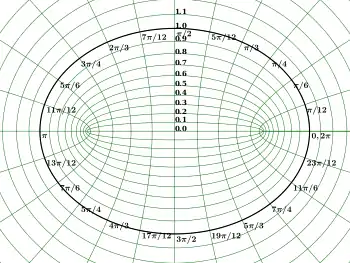
Основное определение
Эллиптические координаты обычно определяются по правилу:
где , .
Таким образом определяется семейство конфокальных эллипсов и гипербол. Тригонометрическое тождество
показывает, что линии уровня являются эллипсами, а тождество из гиперболической геометрии
показывает, что линии уровня являются гиперболами.
Коэффициенты Ламэ
Коэффициенты Ламэ для эллиптических координат равны
Тождества для двойного угла позволяют привести их к виду
Элемент площади равен:
а лапласиан равен
Прочие дифференциальные операторы могут быть получены подстановкой коэффициентов Ламэ в общие формулы для ортогональных координат. Например, градиент скалярного поля записывается:
где
- ,
- .
Другое определение
Иногда используется другое более геометрически интуитивное определение эллиптических координат :
Таким образом, линии уровня являются эллипсами, а линии уровня являются гиперболами. При этом
Координаты имеют простую связь с расстояниями до фокусов и . Для любой точки на плоскости
где — расстояния до фокусов соответственно.
Таким образом:
Напомним, что и находятся в точках и соответственно.
Недостатком этой системы координат является то, что она не отображается взаимно однозначно на декартовы координаты:
Коэффициенты Ламэ
Коэффициенты Ламэ для альтернативных эллиптических координат равны:
Элемент площади равен
а лапласиан равен
Прочие дифференциальные операторы могут быть получены подстановкой коэффициентов Ламэ в общие формулы для ортогональных координат.
Литература
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1974. — 832 с.