Софокусные конические сечения
Софокусные конические сечения — в геометрии конические сечения, обладающие одними и теми же фокусами. Поскольку эллипсы и гиперболы обладают двумя фокусами, то существуют софокусные эллипсы и софокусные гиперболы, а также эллипс и гиперболы могут быть софокусными друг другу. В том случае, когда семейство эллипсов софокусно семейству гипербол, каждый эллипс ортогонально пересекает каждую гиперболу. Параболы обладают только одним фокусом, поэтому принять считать софокусными те параболы, которые имеют общий фокус и одну и ту же ось симметрии. Следовательно, любая точка вне оси симметрии лежит на двух софокусных параболах, пересекающих друг друга под прямым углом.
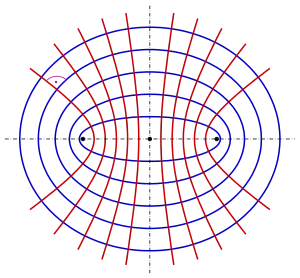
Понятие софокусных конических сечений можно обобщить на трёхмерное пространство, рассматривая софокусные квадрики.
Софокусные эллипсы
Эллипс, не являющийся окружностью, однозначно определяется положением фокусов и точкой вне большой оси. Пучок софокусных эллипсов с фокусами можно описать уравнением
в котором большая полуось является параметром (фокальное расстояние однозначно определяется расположением фокусов). Поскольку точка на эллипсе однозначно задаёт значение , то
- никакие два эллипса в пучке не имеют общих точек.
Софокусные гиперболы
Гипербола однозначно определяется положением фокусов и точкой вне осей симметрии. Пучок софокусных гипербол с фокусами можно описать уравнением
в котором большая полуось является параметром (фокальное расстояние однозначно определяется расположением фокусов). Поскольку точка на гиперболе однозначно задаёт значение , то
- никакие две гиперболы в пучке не имеют общих точек.
Софокусные эллипсы и гиперболы
Уравнение
описывает эллипс при и гиперболу при .
В литературе можно найти другой вариант представления:
где — полуоси данного эллипса (тогда и фокусы заданы) и является параметром пучка.
При мы получаем софокусные эллипсы (то есть ) и
при получаем софокусные гиперболы с фокусами .
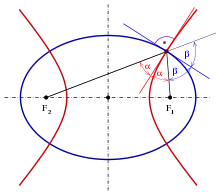
Рассмотрение пучков софокусных эллипсов и гипербол приводит к следующему выводу о касательной и нормали в заданной точке (нормаль к эллипсу и касательная к гиперболе делят пополам угол между направлениями из точки к фокусам):
- каждый эллипс в пучке пересекает каждую гиперболу под прямым углом (см. рисунок).
Таким образом, можно покрыть плоскость ортогональной системой софокусных эллипсов и гипербол. Такую ортогональную сетку можно использовать как основу эллиптической системы координат.
Софокусные параболы

Параболы обладают только одним фокусом. Можно рассматривать параболу как предел пучка софокусных эллипсов или гипербол, у которых один фокус зафиксирован, а второй удаляется на бесконечность. Если подобное рассмотрение провести для софокусных эллипсов и гипербол, можно получить систему из двух пучков софокусных парабол.
Уравнение описывает параболу с началом координат в фокусе, при этом ось x является осью симметрии. Рассмотрим два пучка парабол:
- параболы, бесконечные в правую сторону,
- параболы, бесконечные в левую сторону,
- фокус является общим.
Из уравнения параболы следует, что
- параболы, простирающиеся в одну сторону, не имеют общих точек.
Вычисления показывают, что
- любая парабола , простирающаяся направо, пересекает каждую параболу , простирающуюся налево, ортогонально. Точки пересечения имеют координаты .
Векторы ( являются векторами нормали в точках пересечения. Скалярное произведение данных векторов равно нулю.
По аналогии с софокусными эллипсами и гиперболами, плоскость можно покрыть ортогональной сеткой парабол.
Теорема Грейвса о построении софокусных эллипсов
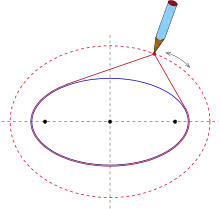
В 1850 году ирландский епископ Чарльз Грейвс доказал и опубликовал следующий метод построения софокусных эллипсов с помощью нити:[1]
- если окружить данный эллипс E кольцом из нити, превышающей по длине контур данного эллипса, нарисуем новый эллипс с помощью закреплённых в фокусах "иголок" (см. построение эллипса), при этом новый эллипс будет софокусным с E. Доказательство данного утверждения требует использования эллиптических интегралов. Отто Штауде обобщил данный метод для построения софокусных эллипсоидов.
Если эллипс E представляет собой отрезок , то софокусные ему эллипсы будут обладать фокусами .
Софокусные поверхности второго порядка
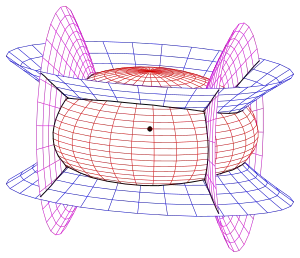
0.1, 0.5, 0.8
Понятие софокусных поверхностей второго порядка является формальным обобщением понятия софокусных конических сечений на трёхмерное пространство.
Выберем три вещественных числа при условии . Уравнение
- описывает
- эллипсоид при ,
- однополостный гиперболоид при (синяя поверхность на рисунке),
- двуполостный гиперболоид при .
- При решений не существует
(В данном контексте параметр не является фокальным расстоянием эллипсоида).
Аналогично случаю софокусных эллипсов/гипербол имеем свойства:
- любая точка при лежит только на одной поверхности каждого из трёх видов софокусных квадрик;
- три поверхности второго порядка, проходящие через точку , пересекаются ортогонально
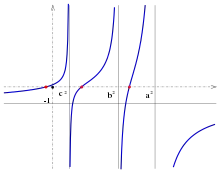
Доказательство существования и единственности трёх квадрик, проходящих через данную точку: для точки при рассмотрим функцию
- .
Данная функция имеет три вертикальные асимптоты и является непрерывной и монотонно возрастающей во всех интервалах . Анализ поведения функции вблизи вертикальных асимптот и при приводит к выводу о том, что имеет три корня при
Доказательство ортогональности поверхностей: рассмотрим пучки функций с параметром . Софокусные квадрики можно описать соотношением . Для любых двух пересекающихся квадрик при в общей точке выполняется равенство
Отсюда скалярное произведение градиентов в общей точке
что доказывает ортогональность.

Приложения.
По теореме Ш. Дюпена об ортогональных системах поверхностей следующие утверждения является справедливым:
- линия пересечения любых двух софокусных поверхностей второго порядка является линией кривизны;
- по аналогии с эллиптическими координатами можно ввести эллипсоидальные координаты.
В физике софокусные эллипсоиды являются эквипотенциальными поверхностями:
- эквипотенциальные поверхности заряженного эллипсоида являются софокусными к данному эллипсоидами.[2]
Теорема Айвори
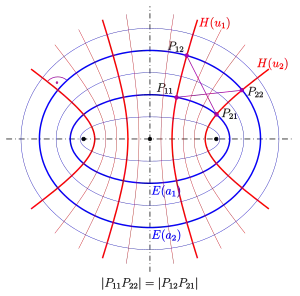
Теорема Айвори, названная по имени шотландского математика Джеймса Айвори (1765–1842), представляет собой утверждение о диагоналях четырёхугольника, образованного ортогональными кривыми.
- В любом четырёхугольнике, образованном двумя софокусными эллипсами и двумя софокусными гиперболами с теми же фокусами, диагонали имеют равные длины.
Точки пересечения эллипса и софокусной гиперболы
Пусть — эллипс с фокусами , задаваемый уравнением
а — софокусная гипербола с уравнением
Вычисление точек пересечения и даёт координаты четырёх точек
Диагонали четырёхугольника
Для упрощения вычислений предположим, что
- , что не является существенным ограничением, поскольку возможно изменение масштаба;
- при выборе знака (см. пункт о точках пересечения) будем рассматривать только . Несложно показать, что выбор другого знака приведёт к тому же результату.
Пусть являются софокусными эллипсами, а являются софокусными гиперболами с теми же фокусами. Диагонали четырёхугольника, образованного точками пересечения с координатами
имеют длины
Последнее выражение является инвариантом по отношению к замене . Подобная замена приводит к выражению для длины . Следовательно, имеет место равенство
Доказательство утверждения для софокусных парабол представляет собой несложные расчёты.
Айвори также доказал теорему для трёхмерного случая:
- у трёхмерного прямоугольного параллелепипеда, образованного софокусными квадриками, диагонали, соединяющие противоположные точки, имеют равные длины.
Примечания
- Felix Klein: Vorlesungen über Höhere Geometrie, Sringer-Verlag, Berlin, 1926, S.32.
- D. Fuchs, S. Tabachnikov: Ein Schaubild der Mathematik. Springer-Verlag, Berlin/Heidelberg 2011, ISBN 978-3-642-12959-9, p. 480.
Литература
- W. Blaschke: Analytische Geometrie. Springer, Basel 1954,ISBN 978-3-0348-6813-6, p. 111.
- G. Glaeser,H. Stachel,B. Odehnal: The Universe of Conics: From the ancient Greeks to 21st century developments, Springer Spektrum, ISBN 978-3-662-45449-7, p. 457.
- David Hilbert & Stephan Cohn-Vossen (1999), Geometry and Imagination, American Mathematical Society, ISBN 0-8218-1998-4
- Ernesto Pascal: Repertorium der höheren Mathematik. Teubner, Leipzig/Berlin 1910, p. 257.
- A. Robson: An Introduction to Analytical Geometry Vo. I, Cambridge, University Press, 1940, p. 157.
- D.M.Y. Sommerville: Analytical Geometry of Three Dimensions, Cambridge, University Press, 1959, p. 235.
Ссылки
- T. Hofmann: Miniskript Differentialgeometrie I, p. 48
- B. Springborn: Kurven und Flächen, 12. Vorlesung: Konfokale Quadriken (S. 22 f.).
- H. Walser: Konforme Abbildungen. p. 8.