Октаэдральные соты порядка 4

В гиперболическом пространстве размерности 3 восьмиугольные соты порядка 4 — правильные паракомпактные соты. Они называются паракомпактными, поскольку имеют бесконечные вершинные фигуры со всеми вершинами как идеальные точки на бесконечности. Если многогранник задан символом Шлефли {3,4,4}, он имеет четыре октаэдра {3,4} вокруг каждого ребра и бесконечное число октаэдров вокруг каждой вершины в квадратном паркете {4,4}, в качестве расположения вершин[1].

octahedral tiling honeycomb порядка 4
Перспективная проекция в модели Пуанкаре
Тип	Гиперболические правильные соты Паракомпактные однородные соты
Символы Шлефли\|{3,4,4} {3,4^1,1}
Диаграммы Коксетера — Дынкина	↔ ↔ ↔
Ячейки	октаэдр {3,4}
Грани	треугольник {3}
Edge figure	квадрат {4}
Вершинная фигура	Квадратный паркет, {4,4}
Двойственные соты	Квадатные мозаичные соты, {4,4,3}
Группы Коксетера	[4,4,3] [3,4^1,1]
Свойства	Правильные

Геометрические соты — это заполняющие пространство многогранники или ячейки большей размерности. Заполнение происходит так, что между ними не остаётся зазоров. Это пример более общего математического понятия мозаики или замощения в пространстве любой размерности.

Соты обычно строятся в обычном евклидовом («плоском») пространстве подобно выпуклым однородным сотам. Их можно построить также в неевклидовых пространствах, такие как однородные гиперболические соты. Любой конечный однородный многогранник может быть спроецирован на его описанную сферу для образования однородных сот в сферическом пространстве.

Симметрия

Построение с половинной симметрией, [3,4,4,1⁺], существует как {3,4^1,1}, с чередованием двух видов (цветов) октаэдральных ячеек. ↔ . Второе построение с половинной симметрией, [3,4,1⁺,4]: ↔ . Более высокий индекс симметрии, [3,4,4^*], индекс 8, существует с пирамидальной фундаментальной областью, [((3,∞,3)),((3,∞,3))]: .

Эти соты содержат , , которые замощают 2-гиперциклические поверхности наподобие паракомпактных мозаик или

Связанные многогранники и соты

Многогранник входит в 15 правильных гиперболических сот в 3-мерном пространстве, 11 из которых, подобно этим сотам, паракомпактны и имеют бесконечные ячейки или вершинные фигуры.

11 паракомпактных правильных сот
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

Имеется пятнадцать однородных сот в [4,4,3] семействе групп Коксетера, включая эту однородную форму.

Семейство сот [4,4,3]
{4,4,3}	r{4,4,3}	t{4,4,3}	rr{4,4,3}	t_0,3{4,4,3}	tr{4,4,3}	t_0,1,3{4,4,3}	t_0,1,2,3{4,4,3}


{3,4,4}	r{3,4,4}	t{3,4,4}	rr{3,4,4}	2t{3,4,4}	tr{3,4,4}	t_0,1,3{3,4,4}	t_0,1,2,3{3,4,4}

Соты являются частью последовательности сот с вершинной фигурой в виде квадратного паркета:

Соты {p,4,4}
Пространство	E³	H³
Форма	Аффинные	Паракомпактные		Некмпактные
Название	{2,4,4}	{3,4,4}	{4,4,4}	{5,4,4}	{6,4,4}	..{∞,4,4}
Coxeter
Image
Cells	{2,4}	{3,4}	{4,4}	{5,4}	{6,4}	{∞,4}

Соты являются частью последовательности правильных четырёхмерных многогранников и сот с октаэдральными ячейками.

Многогранники {3,4,p}
Пространство	S³	H³
Форма	Конечные	Паракомпактные	Некомпактные
Название	{3,4,3}	{3,4,4}	{3,4,5}	{3,4,6}	{3,4,7}	{3,4,8}	... {3,4,∞}
Рисунок
Vertex figure	{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8}	{4,∞}

Спрямлённые восьмиугольные соты порядка 4

Спрямлённые восьмиугольные соты порядка 4

Тип	Паракомпактные однородные соты
Символы Шлефли	r{3,4,4} or t₁{3,4,4}
Диаграммы Коксетера — Дынкина	↔ ↔ ↔
Ячейки	r{4,3} {4,4}
Грани	треугольные {3} квадратные {4}
Вершинная фигура
Группы Коксетера	[4,4,3]
Свойства	вершинно транзитивны

Спрямлённые восьмиугольные соты порядка 4, t₁{3,4,4}, имеют фасеты в виде кубооктаэдра и квадратного паркета, с квадратной пирамидой в качестве вершинной фигуры.

Усечённые восьмиугольные соты порядка 4

Усечённые восьмиугольные соты порядка 4
Тип	Паракомпактные однородные соты
Символы Шлефли	t{3,4,4} или t_0,1{3,4,4}
Диаграммы Коксетера — Дынкина	↔ ↔ ↔
Ячейки	t{3,4} {4,4}
Грани	квадратные {4} шестиугольные {6}
Вершинная фигура
Группы Коксетера	[4,4,3]
Свойства	вершинно транзитивны

Усечённые восьмиугольные соты порядка 4, t_0,1{3,4,4}, имеют фасеты в виде усечённого октаэдра и квадратного паркета с квадратной пирамидой в качестве вершинной фигуры.

Скошенные восьмиугольные соты порядка 4

Скошенные восьмиугольные соты порядка 4
Тип	Паракомпактные однородные соты
Символы Шлефли	rr{3,4,4} или t_0,2{3,4,4} s₂{3,4,4}
Диаграммы Коксетера — Дынкина	↔
Ячейки	rr{3,4} r{4,4}
Грани	треугольник {3} квадрат {4}
Вершинная фигура	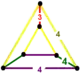треугольная призма
Группы Коксетера	[4,4,3]
Свойства	вершинно транзитивны

Скошенные восьмиугольные соты порядка 4, t_0,2{3,4,4}, имеют грани в виде ромбокубооктаэдра и квадратного паркета с вершинной фигурой в виде треугольной призмы.

Скошено-усечённые восьмиугольные соты порядка 4

Скошено-усечённые восьмиугольные соты порядка 4
Тип	Паракомпактные однородные соты
Символы Шлефли	tr{3,4,4} или t_0,1,2{3,4,4}
Диаграммы Коксетера — Дынкина	↔
Ячейки	tr{3,4} r{4,4}
Грани	квадратные {4} шестиугольные {6} восьмиугольные {8}
Вершинная фигура	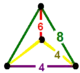тетраэдр
Группы Коксетера	[4,4,3]
Свойства	вершинно транзитивны

Скошено-усечённые восьмиугольные соты порядка 4, t_0,1,2{3,4,4}, имеют фасеты в виде усечённого кубооктаэдра и квадратного паркета с тетраэдром в качестве вершинной фигуры.

Струг-усечённые восьмиугольные соты порядка 4

Струг-усечённые восьмиугольные соты порядка 4
Тип	Паракомпактные однородные соты
Символы Шлефли	t_0,1,3{3,4,4}
Диаграммы Коксетера — Дынкина	↔
Ячейки	t{3,4} rr{4,4}
Грани	треугольник {3} квадрат {4} восьмиугольные {8}
Вершинная фигура	квадратная пирамида
Группы Коксетера	[4,4,3]
Свойства	вершинно транзитивны

Струг-усечённые восьмиугольные соты порядка 4, t_0,1,3{3,4,4}, имеют фасеты в виде усечённого октаэдра и квадратного паркета с квадратной пирамидой в качестве вершинной фигуры.

Плосконосые восьмиугольные соты порядка 4

Плосконосые восьмиугольные соты порядка 4
Тип	Паракомпактные равнобедренные соты
Символы Шлефли	s{3,4,4}
Диаграммы Коксетера — Дынкина	↔ ↔ ↔
Ячейки	квадратный паркет икосаэдр квадратная пирамида
Грани	{3} {4}
Вершинная фигура
Группы Коксетера	[4,4,3⁺] [4^1,1,3⁺] [(4,4,(3,3)⁺)]
Свойства	вершинно транзитивны

Плосконосые восьмиугольные соты порядка 4, s{3,4,4}, имеют диаграмму Коксетера — Дынкина . Они являются равнобедренными сотами с квадратными пирамидами, квадратными мозаиками и икосаэдрами.

См. также

Выпуклые однородные соты в гиперболическом пространстве
Список правильных многомерных многогранников и соединений

Примечания

Coxeter, 1999, с. Chapter 10, Table III.

Литература

Coxeter. Tables I and II: Regular polytopes and honeycombs // Regular Polytopes. — 3rd. ed.. — Dover Publications, 1973. — С. 294–296. — ISBN 0-486-61480-8.
Coxeter. Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — С. 212-213. — ISBN 0-486-40919-8.
Jeffrey R. Weeks. Chapter 16-17: Geometries on Three-manifolds I,II // The Shape of Space. — 2nd. — ISBN 0-8247-0709-5.
N.W. Johnson. Uniform Polytopes. — (Manuscript).
- N.W. Johnson. The Theory of Uniform Polytopes and Honeycombs. — University of Toronto, 1966. — (Ph.D. Dissertation).
- N.W. Johnson. Chapter 13: Hyperbolic Coxeter groups // Geometries and Transformations. — 2015.
- Norman W. Johnson, Asia Ivic Weiss. Quadratic Integers and Coxeter Groups // Can. J. Math.. — 1999. — Т. 51, вып. 6. — С. 1307–1336.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[_bf7ed2078ec17f18-1] Coxeter, 1999, с. Chapter 10, Table III.