Мезоскопическая физика
Мезоскопи́ческая фи́зика или кратко мезоско́пика[1] (от англ. mesoscopics) — раздел физики конденсированных сред, в котором рассматриваются свойства систем на масштабах промежуточных между макроскопическим и микроскопическим. Термин ввёл в 1981 году датский физик Ван Кампен[2]. Многие законы, полученные в макроскопической физике, неприменимы в области мезоскопических размеров, например последовательно соединённые сопротивления нельзя вычислить суммированием отдельных сопротивлений, а следует учитывать квантовые эффекты. Именно мезоскопические размеры накладывают ограничения на классический транспорт в полупроводниках[2]. Мезоскопика возникла в 80-х годал XX века как ответ на технологический прогресс микро- и нанолитографии, роста монокристаллов, а также инструментов типа сканирующего туннельного микроскопа, позволяющего проводить измерения на атомарном уровне[3].
Под микроскопическим масштабом понимают размеры, сравнимые с размерами одного атома или с длиной одной химической связи, то есть с боровским радиусом. Под макроскопическим понимают масштаб, при котором из-за неупругих столкновений теряется квантовая когерентность или фазовая когерентность — то есть становится невозможной интерференция траекторий частиц. Это происходит из-за неупругих столкновений носителей, например при рассеянии на фононах или точечных дефектов, что сбивают фазу волновой функции. Этот размер характеризуется длиной сбоя фазы и обозначается обычно и играет роль характерного масштаба при рассмотрении эффектов, которые приводят к поправкам к проводимости, где важна интерференция, таким как слабая локализация, универсальные флуктуации проводимости, эффект Ааронова — Бома. Одна из задач мезоскопики заключается в учёте таких интерференционных членов в проводимости макроскопических образцов[4].
С точки зрения транспорта в структурах под микроскопическим масштабом следует понимать всякий размер меньше длины свободного пробега носителей тока. Стоит учитывать, что если система обладает макроскопической когерентностью, то это тоже мезоскопическая система, как в случае сверхпроводников. Топологически защищённые состояния, как в случае квантового эффекта Холла, которые можно наблюдать даже при комнатной температуре в графене, тоже мезоскопическая система. Соответственно, мезоскопическая физика изучает явления сильной и слабой локализации, туннелирования и прыжковой проводимости.
Границы макроскопической области существенно зависят от температуры и характера движения частиц (является ли он баллистическим или диффузионным).
Согласно этому определению к мезоскопической физике относятся не только явления в устройствах с мезоскопическими размерами, но и явления в макроскопических устройствах, которые происходят на мезоскопических масштабах, то есть определяются интерференцией. Например, к задачам мезоскопической физики относят нахождение квантовых поправок к сопротивлению макроскопических образцов[4].
Обзор
Квантовая когерентность — основное понятие мезоскопической физики, которое определяется для слабовзаимодействующих квазичастиц в мезоскопических системах движущихся в самосогласованном поле. Оно характеризуется временем фазовой когерентности, связанным с длиной фазовой когеретности, которая типично много больше расстояния между атомами. Длина фазовой когеретности увеличивается при уменьшении температуры, и уменьшается при увеличении количества дефектов в системе. Именно эта длина, которая оказывается порядка размеров изучаемой системы характеризует наличие мезоскопического транспорта в системе[5]. В мезоскопике электронный транспорт описывается в формализме Ландауэра — Бюттикера, который позволяет ответить на вопрос о линейной проводимости или просто проводимости многоконтактных (двухконтактный образец, холловский мост, ван дер Пау геометрия) образцов. Тип контактов (омические, туннельные) приобраетает важное значение при изучении транспорта в мезоскопических образцах. Например, при достаточно малого размера островка и двух туннельных контактов влияние кулоновского взаимодействия приводит к эффекту кулоновской блокады, когда в проводящей системе ток не может течь пока электрон не покинет островок. Если островок имеет размер много больший фермиевской длине волны и много меньше, чем длина свободного пробега возникает транспорт типа бильярда, когда электрон вынужден многократно отражаться от стенок островка прежде чем попасть во второй контакт[6].
Историчеки, мезоскопическая физика изучала вопросы когерентного транспорта в неупорядоченных системах. При достаточно малом размере изучаемых систем (порядка длине фазовой когерентности) проводимость больше не описывалась классической формулой Друде, и возникали квантовые поправки к проводимости, среди которых слабая локализация, эффект Ааронова — Бома, универсальные флуктуации кондактанса. Транспорте в таких системах размера порядка a, при условии
где — фермиевская длина волны, — длина свободного пробега, — длина фазовой когерентности, существенно зависит от беспорядка[7]. По мере того, как прогресс в технологиях и особенно в нанолитографии позволял выращивать всё более чистые материалы и достигать более низкие температуры — размеры мезоскопических систем росли — ведь они ограничены только длиной фазовой когерентности. Появились системы с длиной свободного пробега порядка микрона или десятков микрон[8]. Баллистические структуры демонстрируют необычное поведение в магнитном поле. Например для достаточно малых размеров (геометрия «крест») возможно разрушение квантового эффекта Холла, который славится свой нечувствительностью к дефектам, но в чистых баллистических системах может пропадать[9].
Квантовые поправки к проводимости
Теория Друде
Теория Друде появилась в 1900 году, но основные выражения для некоторых физических величин (для эффекта Холла, высокочастотной проводимости) используют и сейчас, хотя смысл некоторых параметров поменялся из-за современного знания кинетических явлений в металлах и полупроводниках. Уровень Ферми в металлах находится в зоне проводимости — таким образом приложенное электрическое поле ускоряет электроны пока они не испытывают рассеяние из-за дефектов. Теория Друде, в современной трактовке, учитывает усреднение по рассеивателям, вызывающие неупругие столкновения и представляет собой одноэлектронную модель. Для удельной проводимости металла используется следующее выражение[10]
где
- — удельная электрическая проводимость;
- — концентрация электронов;
- — элементарный заряд;
- — время релаксации по импульсам (время, за которое электрон «забывает» о том, в какую сторону двигался);
- — эффективная масса электрона.
Эта формула описывает все размерности, поскольку её размерность изменяется для концентрации. Время релаксании описывает рассеяние на большие углы — в таком случае электрон не движется в направлении приложенного электрического поля. Формула имеет смысл только для классического (или квазиклассического) транспорта, где несущественен вклад квантовых явлений. Согласие с экспериментом удельных проводимостей в квазиклассическом подходе, где электронные транспортные свойства хорошо описываются усреднением по беспорядку. Но в 80-х годах XX века оказалось, что в мезоскопических образцах это не так[11].
Многие квантовые явления, например связанные с интерференцией, в мезоскопике рассматривают как поправки к удельной проводимости заданной формулой Друде.
Эффект Ааронова — Бома
Эффект Ааронова — Бома проявляется в том, что при движении в магнитном поле волновая функция электрона приобретает дополнительный сдвиг фазы равный[12]
где L — обозначает траекторию электрона, dL — элемент длины этой траектории, A — векторный потенциал связанный с магнитным полем, e — элементарный заряд. Если рассмотреть какую-нибудь замкнутую траекторию, эта дополнительная фаза должна повлиять на интерференционную картину. Например, если электрон двигается в проводящем золотом кольце, соединённым с двумя контактами, а магнитное поле B направлено перпендикулярно плоскости кольца, то данная фаза повлияет на интерференцию между путями расположенными в разных каналах кольцевого интерферометра[13]. При достаточно низких температурах будут наблюдаться осцилляции проводимости этой мезоскопической системы при изменении магнитного поля[14]
где S — площадь кольца, h/e — квант магнитного потока.
Слабая локализация
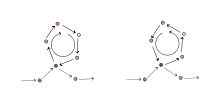
При сильном беспорядке нарушения периодической структуры кристалла настолько велики, что радиус локализации сравним с расстоянием между атомами. Такая система испытывает андерсоновскую локализацию или сильную локализацию и становится непроводящей. При этом произведение длины свободного пробега электрона le и фермиевского импульса становится меньше постоянной Планка (это условие называется критерием Иоффе — Регеля)[15]
В другом пределе электроны делокализованы[16]
волновые функции электрона приобретают вид блоховских волн. Если информация о фазе волновой функции сохраняется порядка времени фазовой когерентности, то все процессы рассеяния сохраняющие фазы приводят к интерференции. В этом длина свободного пробега много меньше длины фазовой когерентности и процесс рассеяния можно отобразить как показано на рисунке. Интерференция возникает для двух возможных путей обходов вдоль траектории[17]. Конструктивная интерференция приводит к увеличению вероятности обнаружить частицу в начале пути — что соответствует увеличению рассеяния или уменьшению проводимости или наоборот деструктивная интерференция соответствует невозможности обнаружить частицы в начале пути, увеличению проводимости. Начальная точка определяется из соотношения неопределённости[18]. Поправка к проводимости для d-мерного случая описывается интегралом[19]
- .
где τ — время релаксации по импульсам, τφ — время фазовой когерентности, D — коэффициент диффузии, λ — де Бройлевская длина волны электрона. Время фазовой когерентности определяется неупругими процессами, то есть меняющими энергию электрона. Рассеяние на электронах и фононах — основные процессы влияющие на τφ. При температурах менее и порядка 1К на время фазовой когерентности влияет электронное рассеяние на электронах, а при больших вклад вносят фононы[20]. Для двумерной системы поправку к проводимости из-за слабой локализации модно записать в виде
Экспериментально для тонких плёнок, любой механизм неупругого рассеяния для времени фазовой когерентности имеет степенную зависимость, поэтому температурная зависимость поправки имеет также логарифмический вид[21].
Универсальные флуктуации кондактанса
Дефазировка
Формализм Бюттикера — Ландауэра
Ландауэр рассмотрел идеальный одномерный случай транспорта в двухконтактном образце с барьером в 1957 году. Идеальность подразумевает отсутствие рассеяния. Единственный источник беспорядка задаётся коэффициентом пропускания барьера T. При коэффициенте пропуская равным единице канал полностью прозрачен. Если ситуация неидеальна, то часть электронов отражается с вероятностью R=1-T. Электронные резервуары подсоединённые с заданными химическими потенциалами поставляют электроны в систему. При разнице в химических потенциалах между правым и левым контактами при прилодении напряжения μ1-μ1=eV возникает ток I в системе[22]. Можно показать, что при нулевой температуре (случай полного вырождения) кондактанс одномерного канала (учтено спиновое вырождение), измеренного между двумя внешними резервуарами, равен
который при идеальном прохождении остаётся конечным и связан с термализацией электронов в контактах. Более строго эта зависимость вычисляется с использованием формулы Кубо[23]. Несмотря на то, что это выражение напоминает обычный закон Ома, интерференция приводит к тому, что результат для двух последовательных барьеров уже не согласуется с классическим результатом и обычно оказывается больше, чем сумма сопротивлений[24].
Одномерный случай представляет собой простейшую задачу о баллистическом транспорте в системе с одним рассеивателем. Она оказывается довольно универсальна когда речь идёт о транспорте в одномерных системах. Для общего случая рассматривают квазиодномерную систему и считают, что система поддерживает N мод, каждая из которых служит отдельным проводящим каналом и проводит ток в соответствии с характеристикой рассеивателей в ситеме. Задача формулируется в терминах многоканального рассеивания, когда мода i может пройти или отразиться с вероятносиями Tij, Rij соответственно в j-тый канал[25]. Полная вероятность прохождения и отражения в канале i задаются выражениеями[26]
В сумме кондактанс многомодовой системы при разности химических потенциалов много меньших теплового размытия (~kT) приобретает вид интеграла по энергии
где f — функция Ферми — Дирака[27].
Квантовый точечный контакт
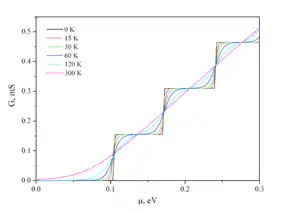
Как показано выше для одномерных проводящих каналов проводимость квантуется. Такая ситуация возникает во многих системах в мезоскопической физике. Нанопроволока или графеновые наноленты, углеродные нанотрубки — это типичные примеры одномерных систем. Существуют также системы, которые формально не являются одномерными, но ведут себя в соответствии с формулой Ландауэра — это система с двумерным электронным газом (ДЭГ) в квантующем магнитном поле и квантовый точечный контакт. Квантовый точечный контакт представляет собой микросужение в ДЭГ сформированное посредством нанолитографии. Его формируют с помощью мезы — полностью удаляют ДЭГ, но это увеличивает количество дефектов по краям проводящего канала или формируют локальные затворы, которые обедняют часть ДЭГ с помощью эффекта поля. Сужение имеет размер сопоставимый с длиной волны электрона, которая определяется законом дисперсии и уровнем Ферми и быть много меньше, чем длина свободного пробега электронов — что приводит к возникновению баллистического транспорта носителей тока в системе. Размер сужения настолько мал, что формирует барьер для электронов, в котором существует несколько квантованных уровней энергии — определяемый квантованием при поперечном движении, зависящем от размера и эффективной массы электронов, но в то же время при движении вдоль канала волновые функции электронов представимы в виде плоских волн. Если уровень Ферми в системе превышает основной уровень квантования в микросужении, то возникает ток в системе. Микросужение характерно тем, что канал сформированный электростатически меняется плавно в зависимости от расстояния до самого узкого места. Это приводит к адиабатическому транспорту — то есть если электрон попадает в область микросужения с достаточной энергией, то он проходит его, тем самым формируя идеальный коэффициент пропускания T=1 для всех мод[28]. Ступеньки в кондактансе полученные из выражение приведено выше принимают вид[29]
где N — это число поперечных мод в микросужении. При повышении температуры наблюдается размытие ступеней в связи с уширением распределения Ферми — Дирака.
Квантовый эффект Холла
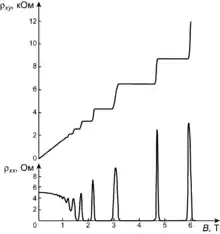
Квантовый эффект Холла наблюдается в двумерной проводящей системе. Эффект заключается в возникновении ступеней со значением холловских сопротивлений — измеренных в геометрии моста Холла — кратным постоянной Клитцинга был открыт в 1980 году в кремнии[30]. Теория Друде хорошо описывает поведение ДЭГ в сильных классических магнитных полях, поскольку как было показано выше в слабых полях возникают поправки к проводимости[31], но из-за квантования спектра электронов в сильном перпендикулярном квантующем магнитном поле ситуация кардинально меняется. Вместо линейной зависимости холловского сопротивления от магнитного формировалась серия ступенек, причём продольная компонента сопротивления обращалась в величину близкую к нулю. В оригинальной работу было показано, что квантование выполнялось с хорошей относительной точностью порядка 1⋅10-7[32]. Возникновение ступенек связано с формированием одномерных проводящих каналов на краях образца, транспорт в которых можно описать в терминах теории Бюттикера — Ландауэра для геометрии холловского моста.
Примечания
- Абрикосов, 1987, с. 200.
- Имри, 2002, с. 11.
- Имри, 2002, с. 12.
- Кульбачинский, 2011.
- Jalabert, 2016, Quantum coherence.
- Jalabert, 2016, Quantum transport.
- Jalabert, 2016, Disordered systems.
- Jalabert, 2016, Ballistic systems.
- Jalabert, 2016, Quenching of the Hall effect.
- Ashcroft & Mermin, 1976, p. 7.
- Akkermans & Montambaux, 2007, p. 4.
- Akkermans & Montambaux, 2007, p. 5.
- Akkermans & Montambaux, 2007, p. 6.
- Akkermans & Montambaux, 2007, p. 7.
- Хмельницкий Д. Е. Андерсоновская локализация // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — 707 с. — 100 000 экз.
- Имри, 2002, с. 20—21.
- Гантмахер, 2013, с. 29.
- Абрикосов, 1987, с. 184.
- Гантмахер, 2013, с. 31—33.
- Абрикосов, 1987, с. 185.
- Гантмахер, 2013, с. 30.
- Имри, 2002, с. 121.
- Имри, 2002, с. 122.
- Имри, 2002, с. 124.
- Имри, 2002, с. 125.
- Имри, 2002, с. 126.
- Имри, 2002, с. 128.
- Имри, 2002, с. 129.
- Имри, 2002, с. 269.
- Имри, 2002, с. 159.
- Имри, 2002, с. 158.
- Имри, 2002, с. 160.
Литература
- Имри Йозеф. Введение в мезоскопическую физику. — М.: Физматлит, 2002. — 304 с. — ISBN 5-9221-0247-8. (рус.)
- Akkermans Eric, Montambaux Gilles. Мезоскопическая физика электронов и фотонов = Mesoscopic Physics of Electrons and Photons. — Cambridge: Cambridge University Press, 2007. — 608 с. — ISBN 9780521349475. (англ.)
- Кульбачинский Владимир Анатольевич. Мезоскопическая физика. http://lomonosov-fund.ru (2 марта 2011). Дата обращения: 19 апреля 2021.
- Jalabert Rodolfo A. (2016). “Mesoscopic transport and quantum chaos”. Scholarpedia. 11 (1): 30946. arXiv:1601.02237. Bibcode:2016SchpJ..1130946J. DOI:10.4249/scholarpedia.30946. (англ.)
- Ashcroft Neil, Mermin N. David. Solid State Physics. — New York : Holt, Rinehart and Winston, 1976. — ISBN 978-0-03-083993-1. (англ.)
- Гантмахер В. Ф. Электроны в неупорядоченных средах. — М.: Физматлит, 2013. — 288 с. — ISBN 978-5-9221-1487-5. (рус.)
- Абрикосов А. А. Основы теории металлов: Учебное руководство. — М.: Наука, Гл. ред. физ. мат. лит., 1987. — 520 с. (рус.)