Волна де Бройля

Физика атомов, молекул и их коллективов, в частности кристаллов, а также атомных ядер и элементарных частиц изучается в квантовой механике. Квантовые эффекты являются существенными, если характерное значение действия (произведение характерной энергии на характерное время или характерного импульса на характерное расстояние) становится сравнимым с ${\displaystyle \hbar }$ (постоянная Планка). Если частицы движутся со скоростями много меньше, чем скорость света в вакууме ${\displaystyle c}$, то применяется нерелятивистская квантовая механика; при скоростях, близких к ${\displaystyle c}$, — релятивистская квантовая механика.

В основе квантовой механики лежат представления Планка о дискретном характере изменения энергии атомов, Эйнштейна о фотонах, данные о квантованности некоторых физических величин (например, импульса и энергии), характеризующих в определённых условиях состояния частиц микромира. В то же время было твёрдо установлено, что свет проявляет свойства не только потока частиц, но и волны, то есть обладает корпускулярно-волновым дуализмом.

Де Бройль выдвинул идею о том, что волновой характер распространения, установленный для фотонов, имеет универсальный характер. Он должен проявляться для любых частиц, обладающих импульсом ${\displaystyle p}$. Все частицы, имеющие конечный импульс ${\displaystyle p}$, обладают волновыми свойствами, в частности, подвержены интерференции и дифракции[4].

Волны де Бройля имеют специфическую природу, не имеющую аналогии среди волн, изучаемых в классической физике: квадрат амплитуды волны де Бройля в данной точке является мерой вероятности того, что частица обнаруживается в этой точке. Дифракционные картины, которые наблюдаются в опытах, являются проявлением статистической закономерности, согласно которой частицы попадают в определённые места в приёмниках — туда, где интенсивность волны де Бройля оказывается наибольшей. Частицы не обнаруживаются в тех местах, где, согласно статистической интерпретации, квадрат модуля амплитуды «волны вероятности» обращается в нуль.

Формула де Бройля устанавливает зависимость длины волны ${\displaystyle \lambda }$, связанной с движущейся частицей вещества, от импульса ${\displaystyle p}$ частицы, а полной энергии ${\displaystyle E}$ — от частоты ${\displaystyle \nu }$, в виде релятивистски инвариантных соотношений:

${\displaystyle \lambda ={\frac {h}{p}},}$

${\displaystyle E=h\nu ,}$

где ${\displaystyle h}$ — постоянная Планка.

Другой вид формул де Бройля:

${\displaystyle \mathbf {p} ={\frac {h}{2\pi }}\mathbf {k} =\hbar \mathbf {k} ,}$

${\displaystyle E=\hbar \omega ,}$

где ${\displaystyle \mathbf {k} ={\frac {2\pi }{\lambda }}\mathbf {n} }$ — волновой вектор, модуль которого ${\displaystyle k={\frac {2\pi }{\lambda }}}$ — волновое число — есть число длин волн, укладывающихся на ${\displaystyle 2\pi }$ единицах длины, ${\displaystyle \omega =2\pi \nu }$ — циклическая частота, ${\displaystyle \mathbf {n} }$ — единичный вектор в направлении распространения волны, ${\displaystyle \hbar ={\frac {h}{2\pi }}\approx 1{,}05\cdot 10^{-34}}$ Дж·с.

Полная энергия ${\displaystyle E=E_{K}+m_{0}c^{2}}$ включает кинетическую энергию ${\displaystyle E_{K}}$ и энергию покоя ${\displaystyle E_{0}=m_{0}c^{2}}$, в терминах которых

${\displaystyle \lambda ={\frac {h}{p}}=hc[E_{K}(E_{K}+2m_{0}c^{2})]^{-1/2},}$

где hc=1240 эВ×нм, и значения ${\displaystyle m_{0}c^{2}}$ равны 0 для фотона и других безмассовых частиц, ${\displaystyle m_{e}c^{2}=}$511 кэВ для электрона, и ${\displaystyle m_{p}c^{2}=}$938 МэВ для протона.

Фазовая скорость волн де Бройля свободной частицы

${\displaystyle v_{f}={\frac {\omega }{k}}={\frac {E}{p}}={\frac {mc^{2}}{mv}}={\frac {c^{2}}{v}}\simeq {\frac {c^{2}}{h}}m\lambda ={\frac {c^{2}p^{2}}{2Wh}}\lambda .}$

Последние соотношения — нерелятивистское приближение. Зависимость фазовой скорости дебройлевских волн от длины волны указывает на то, что эти волны испытывают дисперсию. Фазовая скорость ${\displaystyle v_{f}}$ волны де Бройля хотя и больше скорости света, но относится к числу величин, принципиально неспособных переносить информацию (является чисто математическим объектом).

Групповая скорость волны де Бройля ${\displaystyle u}$ равна скорости частицы ${\displaystyle v}$:

${\displaystyle u={\frac {d\omega }{dk}}={\frac {dE}{dp}}=v}$.

Иллюстрация волны де Бройля

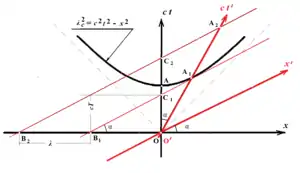
Для частицы массой ${\displaystyle m}$, покоящейся в инерциальной системе отсчёта ${\displaystyle x',ct'}$ псевдоевклидовой плоскости 4-пространства Минковского, движущейся со скоростью ${\displaystyle V}$ относительно условно неподвижной системы ${\displaystyle x,ct}$ вдоль положительного направления оси ${\displaystyle x}$, формула квантовомеханической амплитуды вероятности обнаружить её в каком-либо месте пространства всюду одна и та же. Однако фаза — есть функция времени:

${\displaystyle ae^{(-i\omega _{0})t'}}$,[7]

где: ${\displaystyle \omega _{0}={\frac {E_{0}}{\hbar }}={\frac {mc^{2}}{\hbar }}={\frac {2\pi \cdot c}{\lambda _{C}}}}$;

Здесь: ${\displaystyle \omega _{0}}$ — частота изменения фазы;

${\displaystyle E_{0}}$ — энергия покоящейся частицы;

${\displaystyle \hbar ={\frac {h}{2\pi }}}$ — приведённая постоянная Планка:

${\displaystyle c}$ — скорость света;

${\displaystyle \lambda _{C}={\frac {h}{mc}}}$ — комптоновская длина волны покоящейся частицы массой ${\displaystyle m}$[8].

На рисунке обозначено: ${\displaystyle \lambda _{C}=O'A_{1}}$. Линиями равных фаз в этой системе будут линии одновременности, проведённые через точки временной оси параллельно пространственной оси ${\displaystyle x'}$. Эти линии представляют собой плоскую волну, которая описывается волновой функцией

${\displaystyle \psi _{(x',t')}=ae^{(-i\omega _{0})t'}=ae^{(-i/\hbar )E_{0}t'}}$;

На Рисунке 1 показаны только две линии равных фаз, проведённые через точки ${\displaystyle A_{1}}$ и ${\displaystyle A_{2}}$, в которых фазы амплитуды вероятности имеют то же значение, что и в точке ${\displaystyle O'}$, принятой за начальное. Для нештрихованной системы отсчёта ${\displaystyle x,ct}$ фаза амплитуды вероятности обнаружить частицу в какой-либо точке является уже функцией не только времени, но и пространства[7].

Линии равных фаз системы ${\displaystyle x',ct'}$ пересекают как временную, так и пространственную оси системы ${\displaystyle x,ct}$, разбивая при этом каждую из них на равные отрезки.

Фаза амплитуды вероятности является инвариантной величиной. Это означает, если в штрихованной системе в пространственно-временных точках ${\displaystyle C_{1}}$ и ${\displaystyle B_{1}}$ фаза отличается на целое число ${\displaystyle 2\pi }$ относительно фазы в точке ${\displaystyle O'}$, то и в нештрихованной системе в этих точках фазы должны отличаться на то же число ${\displaystyle 2\pi }$.[8] Отсюда следует, что отрезки по осям ${\displaystyle ct}$ и ${\displaystyle x}$ представляют собой длины волн как во времени, так и в пространстве.

Согласно релятивистской концепции, применяя преобразования Лоренца,[9] из рисунка следует:

${\displaystyle OC_{1}=O'A_{1}{\sqrt {1-(V/c)^{2}}}=cT=\lambda _{C}{\sqrt {1-(V/c)^{2}}}}$,

где: ${\displaystyle T}$ — период изменения фазы в нештрихованной системе. Из последнего равенства этой цепочки равенств следует:

${\displaystyle E=\hbar \omega }$,

где: ${\displaystyle \omega }$ — круговая частота изменения фазы в системе ${\displaystyle x,ct}$;

${\displaystyle E=mc^{2}/{\sqrt {1-(v/c)^{2}}}}$ — полная энергия частицы в системе отсчета ${\displaystyle x,ct}$;

Здесь учтено, что скорость частицы ${\displaystyle v}$ равна скорости ${\displaystyle V}$ перемещения штрихованной системы, в которой эта частица покоится.

Из треугольника ${\displaystyle OB_{1}C_{1}}$, принимая во внимание, что ${\displaystyle \operatorname {tg\alpha } ={\frac {V}{c}}}$ и учитывая, что ${\displaystyle v=V}$, получим:

${\displaystyle B_{1}O={\frac {\lambda _{C}{\sqrt {1-(v/c)^{2}}}}{\operatorname {tg\alpha } }}={\frac {h}{p}}=\lambda }$,

где: ${\displaystyle \lambda }$ — длина волны де Бройля;

${\displaystyle p}$ — импульс частицы.

Выражение для фазы амплитуды вероятности волны де Бройля в системе ${\displaystyle x,ct}$ можно получить, используя преобразование Лоренца для времени при переходе из штрихованной системы к нештрихованной:

${\displaystyle t'={\frac {t-(V/c^{2})x}{\sqrt {1-(V/c)^{2}}}}}$;

Заменив ${\displaystyle t'}$ на ${\displaystyle t}$ в выражении для амплитуды в штрихованной системе отсчета, получим:

${\displaystyle ae^{(-i/\hbar )E_{0}t'}=ae^{-{(i/\hbar )\left[\left(E_{0}t/{\sqrt {1-(V/c)^{2}}}\right)-\left(E_{0}Vx/{c^{2}{\sqrt {1-(V/c)^{2}}}}\right)\right]}}}$;

Отождествляя полную энергию частицы ${\displaystyle E=E_{0}/{\sqrt {1-(v/c)^{2}}}}$ и её импульс ${\displaystyle p=E_{0}v/c^{2}{\sqrt {1-(v/c^{2}}}}$ с полученным при преобразовании выражением для фазы, учитывая, что ${\displaystyle v=V}$, формула амплитуды волны де Бройля запишется так:

${\displaystyle ae^{-{(i/\hbar )\left[Et-px\right]}}}$;[7]

Фазовая скорость волны, то есть скорость, с которой перемещаются точки волны с постоянной фазой (например, на Рисунке 1 перемещение одноимённой фазы из точки ${\displaystyle B_{1}}$ в точку ${\displaystyle C_{1}}$) определяется непосредственно из треугольника ${\displaystyle OB_{1}C_{1}}$:

${\displaystyle v_{f}={\frac {c^{2}}{v}}}$;

Монохроматическая волна де Бройля характеризуется соотношениями ${\displaystyle \Delta x=\infty }$ и ${\displaystyle \Delta p=0}$. То есть, такой волновой объект имеет вполне определённый импульс и совершенно неопределённую область локации.[10] Именно это и содержится в утверждении, когда говорится, что существует одинаковая амплитуда вероятности обнаружить частицу во всех точках пространства.

Явление корпускулярно-волнового дуализма присуще всем видам материи, но в разной степени. Частице массой ${\displaystyle m=10^{-5}}$ г, движущейся со скоростью ${\displaystyle v=1}$ м/с, соответствует волна де Бройля с длиной волны ${\displaystyle \lambda =6{,}6\cdot 10^{-22}}$ см. Такие длины волн лежат за пределами доступной наблюдению области. Поэтому в механике макроскопических тел волновые свойства несущественны и не учитываются.[8]

Гипотеза де Бройля объясняет ряд экспериментов, необъяснимых в рамках классической физики[11]:

• Опыт Дэвиссона — Джермера по дифракции электронов на кристаллах никеля.
• Опыт Дж. П. Томсона по дифракции электронов на металлической фольге.
• Эффект Рамзауэра аномального уменьшения сечения рассеяния электронов малых энергий атомами аргона.
• Дифракция нейтронов на кристаллах (опыты Г. Хальбана, П. Прайсверка и Д. Митчелла).

Волновые свойства не проявляются у макроскопических тел. Длины волн де Бройля для таких тел настолько малы, что обнаружение волновых свойств оказывается невозможным. Впрочем, наблюдать квантовые эффекты можно и в макроскопическом масштабе, особенно ярким примером этому служат сверхпроводимость и сверхтекучесть.

• Волновой пакет
• Комптоновская длина волны
• Ток вероятности

• Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Вып. 3–4. — 3-е изд. — М.: Мир, 1976. — 496 с.
• www.e-libra.su/read/464761-tom-3-kvantovaya-mehanika.html# — Фейнман Ричард Филлипс. Том 3. Квантовая механика читать онлайн. Гл. 5. § 1, § 2.

• Волны де Бройля / лекция «Элементы квантовой механики»
• Соотношение де Бройля // «Элементы»