Квантовый точечный контакт
Квантовый точечный контакт (КТК) — узкое сужение между двумя широкими электропроводящими областями, ширина которого сопоставима с длиной волны электронов (от нанометров до микрометров)[2].
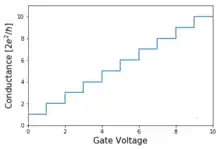
Важность КТК заключается в том, что они доказывают квантование баллистической проводимости в мезоскопических системах. Проводимость КТК квантуется в единицах , так называемый квантах проводимости.
Впервые о квантовых точечных контактах сообщили в 1988 году голландская группа из Делфтского технологического университета и Philips Research[1] и, независимо, британская группа из Кавендишской лаборатории[3]. Они основаны на более ранней работе британской группы, которая показала, как можно использовать разделённые вентили для преобразования двумерного электронного газа в одномерный канал сначала в кремнии[4], а затем в арсениде галлия[5][6].
Это квантование подобно квантованию холловской проводимости, но измеряется в отсутствие магнитного поля. Квантование проводимости в нулевом поле и плавный переход к квантовому эффекту Холла при приложении магнитного поля по существу являются следствием равнораспределения тока между целым числом распространяющихся мод в сужении.
Изготовление
Есть несколько различных способов изготовления квантового точечного контакта. Это может быть реализовано в разрывном соединении, если разорвать кусок металлического проводника до тех пор, пока он не сломается. Точка разрыва образует точечный контакт. В более контролируемом методе, квантовые точечные контакты выполнены в виде двумерного электронного газа (2DEG), например, в GaAs/AlGaAs гетероструктурах. Путем подачи напряжения на затворные электроды подходящей формы электронный газ может быть локально обеднён, и в плоскости 2DEG можно создать много различных типов проводящих областей, в том числе квантовые точки и квантовые точечные контакты. Другой способ создания КТК — это размещение наконечника сканирующего туннельного микроскопа близко к поверхности проводника.
Характеристики
Геометрически квантовый точечный контакт представляет собой сужение в поперечном направлении, которое оказывает сопротивление движению электронов. Подача напряжения через точечный контакт вызывает прохождение тока, величина этого тока определяется выражением , где — проводимость контакта. Эта формула напоминает закон Ома для макроскопических резисторов. Однако здесь есть принципиальная разница, связанная с малым размером системы, что требует квантово-механического анализа[7].
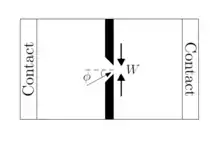
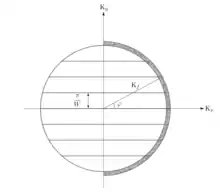
Наиболее распространено изучение КТК в двумерных электронных газах. Таким образом, геометрическое сужение точечного контакта превращает проводимость через отверстие в одномерную систему. Более того, это требует квантово-механического описания системы, которое приводит к квантованию проводимости. Квантово-механически ток через точечный контакт равномерно распределяется между одномерными подзонами или поперечными модами в сужении.
Важно отметить, что предыдущее обсуждение не принимает во внимание возможные переходы между модами (нет рассеяния). Формулу Ландауэра можно обобщить, чтобы выразить эти возможные переходы
,
где — матрица перехода, которая включает ненулевые вероятности перехода из моды n в моду m .
При низких температурах и напряжениях нерассеянные и незахваченные электроны (на ловушках), вносящие вклад в ток, имеют определённую энергию/импульс/длину волны, называемую энергией/импульсом/длиной волны Ферми. Как и в волноводе, поперечное ограничение в квантовом точечном контакте приводит к «квантованию» поперечного движения — поперечное движение не может изменяться непрерывно, но должно принимать вид одной из серии дискретных мод. Аналогия с волноводом применима до тех пор, пока когерентность не теряется из-за рассеяния, например, на дефекте или ловушке. Электронная волна может пройти через сужение только в том случае, если она конструктивно интерферирует, что для данной ширины сужения происходит только для определённого количества мод . Ток, переносимый таким квантовым состоянием, является произведением скорости на плотность электронов. Эти две величины сами по себе различаются от одной моды к другой, но их произведение не зависит от моды. Как следствие, каждое состояние вносит одинаковое количество для каждого спина в полную проводимость системы .
Это фундаментальный результат; проводимость не принимает произвольных значений, а квантуется кратно кванту проводимости , который выражается через заряд электрона и постоянную Планка . Целое число определяется шириной точечного контакта и примерно равна ширине, деленной на половину длины волны электрона. В зависимости от ширины точечного контакта (или напряжения затвора в случае устройств с гетероструктурой GaAs/AlGaAs) проводимость демонстрирует ступенчатое поведение, поскольку все больше и больше мод (или каналов) вносят вклад в перенос электронов. Высота ступеньки определяется выражением .
Экспериментально при повышении температуры обнаруживается, что плато приобретают конечный наклон до тех пор, пока не перестаёт разрешаться. Это следствие термического размытия распределения Ферми — Дирака. Ступеньки проводимости должны исчезнуть при температуре (для GaAs/AlGaAs) (здесь ∆E — расщепление подзоны на уровне Ферми). Это подтверждается как экспериментом, так и численными расчетами[8].
Внешнее магнитное поле, приложенное к квантовому точечному контакту, снимает вырождение по спину и приводит к полуцелым ступеням проводимости. Кроме того, количество мод, которые вносят вклад, становится меньше. Для больших магнитных полей не зависит от ширины сужения, и задаётся другой теорией квантового эффекта Холла. Интересной особенностью, является плато на , так называемая 0,7-аномалия связанная с электрон-электронным взаимодействием.
Приложения
Помимо изучения основ переноса заряда в мезоскопических проводниках, квантовые точечные контакты могут использоваться в качестве чрезвычайно чувствительных детекторов заряда. Поскольку проводимость через контакт сильно зависит от размера сужения, то любые колебания потенциала (например, создаваемые другими электронами) поблизости будут влиять на ток через КТК. По такой схеме возможно обнаружение одиночных электронов. В связи с квантовыми вычислениями в твердотельных системах КТК могут использоваться в качестве устройств считывания состояния квантового бита (кубита)[9][10][11][12]. В физике конфигурация КТК используется для демонстрации полностью баллистического полевого транзистора[13]. Ещё одно применение устройства — его использование в качестве переключателя. Никелевая проволока подводится достаточно близко к поверхности золота, а затем с помощью пьезоэлектрического привода расстояние между проволокой и поверхностью может быть изменено, и, таким образом, транспортные характеристики устройства меняются между туннелированием электронов и баллистическим[14].
Примечания
- B.J. van Wees (1988). “Quantized conductance of point contacts in a two-dimensional electron gas”. Physical Review Letters. 60 (9): 848&ndash, 850. Bibcode:1988PhRvL..60..848V. DOI:10.1103/PhysRevLett.60.848. PMID 10038668.
- H. van Houten (1996). “Quantum point contacts”. Physics Today. 49 (7): 22&ndash, 27. arXiv:cond-mat/0512609. Bibcode:1996PhT....49g..22V. DOI:10.1063/1.881503.
- D.A. Wharam (1988). “One-dimensional transport and the quantization of the ballistic resistance”. J. Phys. C. 21 (8): L209—L214. Bibcode:1988JPhC...21L.209W. DOI:10.1088/0022-3719/21/8/002.
- C.C.Dean and M. Pepper (1982). “The transition from two- to one-dimensional electronic transport in narrow silicon accumulation layers”. J. Phys. C. 15 (36): L1287—L1297. Bibcode:1982JPhC...15.1287D. DOI:10.1088/0022-3719/15/36/005.
- T. J. Thornton (1986). “One-Dimensional Conduction in the 2D Electron Gas of a GaAs-AlGaAs Heterojunction”. Physical Review Letters. 56 (11): 1198—1201. Bibcode:1986PhRvL..56.1198T. DOI:10.1103/PhysRevLett.56.1198. PMID 10032595.
- K-F. Berggren (1986). “Magnetic Depopulation of 1D Subbands in a Narrow 2D Electron Gas in a GaAs:AlGaAs Heterojunction”. Physical Review Letters. 57 (14): 1769—1772. Bibcode:1986PhRvL..57.1769B. DOI:10.1103/PhysRevLett.57.1769. PMID 10033540.
- Pearsall. Quantum Photonics, 2nd edition. — ISBN 978-3-030-47324-2. — doi:10.1007/978-3-030-47325-9.
- C.W.J.Beenakker and H. van Houten (1991). “Quantum Transport in Semiconductor Nanostructures”. Solid State Physics. 44: 1—228. arXiv:cond-mat/0412664. Bibcode:2004cond.mat.12664B. DOI:10.1016/s0081-1947(08)60091-0.
- J.M. Elzerman (2003). “Few-electron quantum dot circuit with integrated charge read out”. Physical Review B. 67 (16): 161308. arXiv:cond-mat/0212489. Bibcode:2003PhRvB..67p1308E. DOI:10.1103/PhysRevB.67.161308.
- M. Field (1993). “Measurements of Coulomb blockade with a noninvasive voltage probe”. Physical Review Letters. 70 (9): 1311—1314. Bibcode:1993PhRvL..70.1311F. DOI:10.1103/PhysRevLett.70.1311. PMID 10054344.
- J. M. Elzerman (2004). “Single-shot read-out of an individual electron spin in a quantum dot”. Nature. 430 (6998): 431—435. arXiv:cond-mat/0411232. Bibcode:2004Natur.430..431E. DOI:10.1038/nature02693. PMID 15269762.
- J. R. Petta (2005). “Coherent Manipulation of Coupled Electron Spins in Semiconductor Quantum Dots”. Science. 309 (5744): 2180—2184. Bibcode:2005Sci...309.2180P. DOI:10.1126/science.1116955. PMID 16141370.
- E. Gremion (2010). “Evidence of a fully ballistic one-dimensional field-effect transistor: Experiment and simulation”. Applied Physics Letters. 97 (23): 233505. Bibcode:2010ApPhL..97w3505G. DOI:10.1063/1.3521466.
- Smith, D. P. E. (1995). “Quantum Point Contact Switches”. Science. 269 (5222): 371—3. Bibcode:1995Sci...269..371S. DOI:10.1126/science.269.5222.371. PMID 17841257. Дата обращения 30 May 2020.
Литература
- C.W.J.Beenakker and H. van Houten (1991). “Quantum Transport in Semiconductor Nanostructures”. Solid State Physics. 44: 1—228. arXiv:cond-mat/0412664. Bibcode:2004cond.mat.12664B. DOI:10.1016/s0081-1947(08)60091-0.
- K. J. Thomas (1996). “Possible spin polarization in a one-dimensional electron gas”. Physical Review Letters. 77 (1): 135—138. arXiv:cond-mat/9606004. Bibcode:1996PhRvL..77..135T. DOI:10.1103/PhysRevLett.77.135. PMID 10061790.
- Nicolás Agraït (2003). “Quantum properties of atomic-sized conductors”. Physics Reports. 377 (2—3): 81. arXiv:cond-mat/0208239. Bibcode:2003PhR...377...81A. DOI:10.1016/S0370-1573(02)00633-6.
- Timp. Semiconductors and Semimetals Volume 35. — 1992. — Vol. 35. — P. 113–190. — ISBN 9780127521350. — doi:10.1016/S0080-8784(08)62393-5.