Граф Аполлония
Граф Аполлония[1] — неориентированный граф, образованный рекурсивным процессом подразделения треугольника на три меньших треугольника. Графы Аполлония можно эквивалентно определить как планарные 3-деревья, как максимальные планарные хордальные графы, как однозначно 4-раскрашиваемые планарные графы или как графы блоковых многогранников. Графы названы именем Аполлония Пергского, изучавшего связанные построения упаковки кругов.
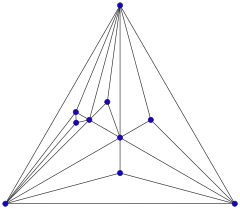

Определение
Граф Аполлония может быть получен из треугольного графа, вложенного в евклидову плоскость, путём неоднократного выбора треугольной грани вложения, добавления новой вершины в эту треугольную грань и соединения новой вершины с каждой вершиной внутри грани. В результате грань делится на три меньших треугольника, которые, в свою очередь, могут быть поделены тем же самым образом.
Примеры
Полные графы с тремя и четырьмя вершинами, K3 и K4, являются графами Аполлония. K3 образуется начальным треугольником без дальнейших операций подразделения граней, в то время как K4 образуется одной операцией подразделения.
Граф Голднера — Харари является графом Аполлония, а также наименьшим негамильтоновым максимальным планарным графом[2]. Другой, более сложный граф Аполлония, использовал Нишизеки[3] как пример 1-жёсткого негамильтонова максимального планарного графа.
Теоретические свойства
Поскольку графы Аполлония определяются рекурсивным подразделением треугольников, они имеют другие математические описания. Графы являются хордальными максимальными планарными графами, хордальными полиэдральными графами и планарными 3-деревьями. Графы являются однозначно 4-раскрашиваемыми планарными графами и планарными графами с уникальной декомпозицией в лес Шнайдера, состоящий из трёх деревьев. Графы являются максимальными планарными графами с древесной шириной три, классом графов, которые можно описать их запрещёнными графами или их сведением путём Y-Δ преобразований. Графы являются максимальными планарными графами с вырожденностью три. Графы являются также планарными графами с данным числом вершин, которые имеют наибольшее возможное число треугольников, наибольшее возможное число тетраэдральных подграфов, наибольшее возможное число клик и наибольшее возможное число частей после разложения на отдельные треугольники.
Хордальность
Графы Аполлония являются примерами максимальными планарными графами, в которые нельзя добавить ребро без нарушения планарности, или, эквивалентно, графами, которые могут быть нарисованы на плоскости так, что любая грань (включая внешнюю грань) является треугольником. Графы являются также хордальными графами, в которых каждый цикл из четырёх или более вершин имеет диагональное ребро, соединяющее две вершины цикла, не являющиеся последовательными в цикле, а порядок, в котором вершины добавляются в процессе построения графа Аполлония, является порядком исключения в хордальном графе. Это свойство даёт альтернативное описание графов Аполлония — это в точности хордальные максимальные планарные графы или, эквивалентно, хордальные полиэдральные графы[4].
В графе Аполлония любая максимальная клика — это полный граф с четырьмя вершинами, образованный выбором любой вершины и трёх ближайших соседей. Любой минимальный кликовый сепаратор (клика, удаление которой разбивает граф на два несвязных графа) — это один из разделённых треугольников. Хордальный граф, в котором все максимальные клики и все минимальные кликовые сепараторы имеют один и тот же размер, является k-деревом, а графы Аполлония являются примерами 3-деревьев. Не все 3-деревья планарны, но планарные 3-деревья — это в точности графы Аполлония.
Единственность раскраски
Любой граф Аполлония имеет единственную 4-цветную раскраску. Поскольку граф планарен, из теоремы о четырёх красках следует, что граф имеет раскраску четырьмя цветами, но поскольку цвета начального треугольника фиксированы, имеется единственная возможность выбора цвета для новой вершины, так что с точностью до перестановки цветов раскраска графа будет единственной. Труднее показать, но это также верно, что любой планарный граф с единственной раскраской является графом Аполлония. Таким образом, граф Аполлония может быть охарактеризован как планарный граф с единственной 4-цветной раскраской[5]. Графы Аполлония дают примеры планарных графов, имеющих минимальное число k-раскрасок для k > 4[6]
Также графы Аполлония — это в точности максимальные планарные графы, которые (если фиксировать внешнюю грань) имеют единственный лес Шнайдера, разбиение рёбер графа на три дерева с корнями в вершинах внешней грани[7][8].
Древесная ширина
Графы Аполлония не образуют семейство графов, замкнутого относительно операции взятия миноров графа, так как при удалении рёбер, но не вершин, получим граф, не являющийся графом Аполлония. Тем не менее, семейство планарных частичных 3-деревьев, подграфов графов Аполлония, является минорно замкнутым семейством. Таким образом, согласно теореме Робертсона — Сеймура, они могут быть охарактеризованы конечным числом запрещённых миноров. Минимальные запрещённые миноры для планарных частичных 3-деревьев — это четыре минимальных графа для планарных графов и частичных 3-деревьев: полный граф K5, полный двудольный граф K3,3, граф октаэдра и граф пятиугольной призмы. Графы Аполлония являются максимальными графами, которые не содержат эти четыре графа в качестве миноров[9]
Преобразование Y-Δ, заменяющее вершину степени три на треугольник, соединяющий соседей, достаточно (вместе с операцией удаления кратных рёбер) для сведения графа Аполлония к единственному треугольнику. Планарные графы, которые могут быть сведены к единственному ребру с помощью преобразования Y-Δ, удаления кратных рёбер, удаления вершин степени 1 и заменой вершины степени 2 вместе с рёбрами на одно ребро, это в точности планарные частичные 3-деревья. Двойственные графы планарных частичных 3-деревьев образуют другое замкнутое относительно взятия миноров семейство графов, которое является в точности теми графами, которые можно свести к единственному ребру с помощью преобразования Δ-Y, удаления кратных рёбер, удаления вершин степени 1, и избавления от вершин степени 2[10].
Вырожденность
В любом подграфе графа Аполлония последняя добавленная вершина имеет степень три, так что графы Аполлония имеют вырожденность три. Порядок, в котором вершины добавляются при создании графа, таким образом, являются порядком вырождения и графы Аполлония совпадают с 3-вырожденными максимальными планарными графами.
Экстремальность
Другое свойство, характеризующее графы Аполлония, связано со связностью. Любой максимальный планарный граф может быть разложен на вершинно 4-связные максимальные планарные подграфы путём разделения вдоль треугольников (не являющихся гранями графа) — если имеется треугольник, не являющийся гранью, можно образовать два меньших максимальных планарных графа, один состоит из части, находящейся внутри треугольника, другой состоит из внешней по отношению к треугольнику части. Максимальные планарные графы без разделяющих треугольников, которые образуются многократным разбиением такого рода, иногда называют блоками, хотя то же имя используется и для компонент двусвязности графа, который сам по себе двусвязным не является. Граф Аполлония — это максимальный планарный граф, в котором все блоки изоморфны полному графу K4.
В экстремальной теории графов графы Аполлония — это в точности планарные графы с n вершинами, в которых число блоков достигает максимального значения n − 3, и планарные графы, в которых число треугольником максимально и равно 3n − 8. Поскольку каждый подграф K4 планарного графа должен быть блоком, на этих графах достигается максимум числа подграфов K4 (это число равно n − 3). На этих же графах достигается максимальное число клик любого типа (число клик равно 8n − 16)[11]
Геометрические реализации
Построение из упаковки кругов
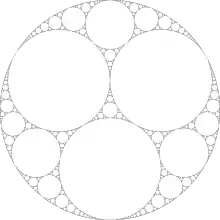

Графы названы именем Аполлония Пергского, изучавшего задачу построения окружностей, касающихся трёх других окружностей. Один из методов построения графов Аполлония — начать с трёх взаимно касающихся окружностей и многократно вписывать другую окружность в промежуток, образованный тремя окружностями, построенными до этого. Фрактал, образованный таким образом, называется сеткой Аполлония.
Если процесс построения сетки Аполлония остановить, нарисовав лишь конечное число окружностей, то граф, имеющий вершину для каждой окружности и ребро для любых двух касающихся окружностей, и есть граф Аполлония[12]. Существование множества касающихся окружностей, касания которых представляют граф Аполлония, определяется теоремой Кёбе — Андреева — Тёрстона, которая утверждает, что любой планарный граф может быть представлен касающимися окружностями[13].
Многогранники
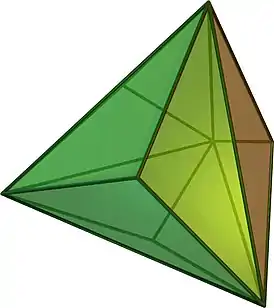
Графы Аполлония — это планарные вершинно 3-связные графы, и потому, по теореме Штайница, могут быть всегда представлены как графы выпуклых многогранников. Выпуклый многогранник, представляющий граф Аполлония — это 3-мерный блоковый многогранник. Такие многогранники могут быть получены из тетраэдра многократным приклеиванием дополнительных тетраэдров (по одному) к треугольным граням многогранника. Таким образом, графы Аполлония могут быть определены как графы блоковых 3-мерных многогранников[14]. Можно найти представление любого графа Аполлония как выпуклого 3-мерного многогранника, в котором все координаты являются целыми числами полиномиальной величины, что лучше, чем для других планарных графов[15].
Треугольные сетки
Рекурсивное разделение треугольников на три меньших треугольников исследовали Элкок, Гаргантини и Волш в качестве техники сегментации изображения в компьютерном зрении[16]. В этом контексте они называют такое разделение тройным неравносторонним разложением на треугольники. Они заметили, что при добавлении каждой новой вершины в центроид в треугольник треугольники триангуляции будут иметь одинаковые площади, хотя они и не одинаковой формы. Более обще, графы Аполлония можно нарисовать на плоскости с любой заранее заданной площадью каждой грани. Если площади заданы как рациональные числа, такими будут и координаты вершин[17].
Можно провести процесс деления треугольников при построении графа Аполлония таким образом, что на каждом шаге длины рёбер будут рациональными числами. Неизвестно, можно ли нарисовать любой планарный граф с теми же свойствами[18]. За полиномиальное время можно найти рисунок планарного 3-дерева с целыми координатами с минимальной площадью ограничивающего прямоугольника и проверить, можно ли нарисовать заданное планарное 3-дерево с вершинами на заданном множестве точек[19]
Свойства и приложения
Графы без совершенного паросочетания
Пламмер[20] использовал графы Аполлония для построения бесконечного семейства максимальных планарных графов с чётным числом вершин, не имеющих совершенного паросочетания. Графы Пламмера строятся в два этапа. На первом этапе, начиная с треугольника abc, многократно повторяется деление треугольной грани, содержащей ребро bc. Результирующий граф содержит путь из a до конечной вершины деления и каждая вершина этого пути соединена рёбрами с вершинами b и c. На втором этапе каждая (треугольная) грань полученного планарного графа ещё раз разбивается. Если путь из a до конечной вершины разбиения первого этапа имеет чётную длину, общее число вершин графа тоже чётно. Однако примерно 2/3 вершин, вставленные на втором этапе, образуют независимое множество и не могут составлять паросочетание друг с другом, а оставшихся вершин для образования совершенного паросочетания недостаточно.
Хотя сами по себе графы Аполлония не могут иметь совершенных паросочетаний, двойственные графам Аполлония графы являются 3-регулярными графами без разрезающих рёбер, так что по теореме Петерсена[21] они обязательно имеют по меньшей мере одно совершенное паросочетание. Для графов Аполлония известно даже больше — двойственные графам Аполлония графы имеют экспоненциально большое число совершенных паросочетаний[22]. Ласло Ловас и Майкл Д. Пламмер высказали гипотезу, что аналогичная экспоненциальная нижняя граница должна существовать для всех 3-регулярных графов без разрезающих рёбер, что было позднее подтверждено.
Степенной закон графов
Ж. Андраде, Г. Геррманн, Р. Андраде и Л. де Сильва[12] изучали степенные законы последовательностей степеней специальных видов графов этого вида, образованных делением всех треугольников одинаковое число раз. Они использовали эти графы для моделирования заполнения пространства частями различного размера. Основываясь на их работе, другие авторы предложили случайные графы Аполлония, получаемые случайным выбором грани для деления, и показали, что для этих графов выполняется степенной закон в распределении степеней вершин[23], а также показали, что эти графы имеют малые расстояния[24][25]. Фриз и Тсоуракакис анализировали наибольшие степени вершин и собственные значения случайных графов Аполлония[26]. Ж. Андраде, Г. Геррманн, Р. Андраде и Л. де Сильва заметили также, что их графы удовлетворяют эффекту «мир тесен» (теория шести рукопожатий), то есть что все вершины находятся на близком расстоянии друг от друга. Основываясь на численных экспериментах, они оценили среднее расстояние между случайно выбранными парами вершин в графе с n вершинами как пропорциональное (log n)3/4, но дальнейшие исследования показали, что среднее расстояние на самом деле пропорционально log n[27][28].
Распределение углов
Батлер и Грэм[29] заметили, что если каждая новая вершина помещается в точку пересечения биссектрис треугольника, то множество троек углов треугольников в подразделении, если их интерпретировать как барицентрические координаты точек в правильном треугольнике, в пределе образует треугольник Серпинского при росте уровня подразделения.
Гамильтоновость
Такео[30] ошибочно утверждал, что все графы Аполлония имеют гамильтоновы циклы, однако граф Голднера–Харари служит контрпримером. Если граф Аполлония имеет жёсткость, большую единицы (что означает, что при удалении любого числа вершин из графа в графе остаётся связных компонент меньше, чем число удалённых вершин), он обязательно гамильтонов, но существуют негамильтоновы графы Аполлония, если жёсткость равна единице[31]
Перечисление
Задачу комбинаторики подсчёта аполлониевых триангуляций изучал Такео[30]. Он показал, что для числа триангуляций существует простая производящая функция f(x), описываемая равенством f(x) = 1 + x(f(x))3. В этой производящей функции член степени n содержит число графов Аполлония с внешним треугольником и n + 3 вершинами. Число графов Аполлония (с внешним треугольником) и 3, 4, 5, … вершинами:
Эта же последовательность задаёт число троичных деревьев и число разбиений выпуклого многоугольника на многоугольники с нечётным числом сторон. Например, существует 12 графов Аполлония с 6 вершинами — три образуются разбиением внешнего треугольника с последующим разбиением двух из полученных треугольников и ещё девять образуются разбиением внешнего треугольника и разбиением одного из полученных треугольников с последующим разбиением одного из маленьких треугольников.
История
У Биркгофа[32] есть ранняя статья, в которой используется двойственная форма графов Аполлония, планарные карты, образованные многократным помещением новых областей в вершинах более простых карт, в качестве примера класса планарных графов с малым числом цветов.
Геометрические структуры, близкие графам Аполлония, изучлись в комбинаторике многогранников с начала 1960-х годов, когда их использовал Грюнбаум[33] для описания графов, которые можно реализовать в многогранниках единственным образом по размерности и с точки зрения комбинаторики. Их использовали также Мун и Мозер[34] для поиска симплициальных многогранников без длинных путей. В теории графов тесная связь между планарностью и древесной шириной прослеживается к статье Робертсона и Сеймура 1984 года[35], которые показали, что замкнутое относительно взятия миноров семейство графов либо имеет ограниченную древесную ширину, либо содержит все планарные графы. Планарные 3-деревья, как класс графов, рассматривали Хакими и Шмайхель[36], Алон и Каро[37], Патил[38] и многие другие авторы вслед за ними.
Название «граф Аполлония» было предложено в статье Ж. Андраде, Г. Геррманна, Р. Андраде и Л. де Сильва[12] для графов, в которых уровень деления треугольников однороден. Геометрически эти графы соответствуют блоковым многогранникам (многогранникам Кли)[33][39]. Другие авторы использовали термин для более широкого класса графов, планарных 3-деревьев, с целью обобщения модели на случайные графы Аполлония[24][25]. Трианкуляризация, полученная таким образом, была также названа «блоковой триангуляризацией»[37][40][41][7][27][8][22].
См. также
- Барицентрическое подразделение, другой метод деления треугольника на меньшие треугольники
- Лууповское подразделение поверхности, ещё один метод деления треугольника на меньшие треугольники
Примечания
- На английском существует два термина — Apollonian network и Apollonian gasket, оба термина на русский можно перевести как сеть Аполлония. Для второго термина есть статья «Сетка Аполлония». Для первого термина в данной статье используется название «Граф Аполлония»
- Этот граф назван именами авторов статьи(Goldner, Harary 1975). Однако он и раньше появлялся в литературе, например у Грюнбаума (Grünbaum 1967), стр. 357.
- Nishizeki, 1980.
- Эквивалентность планарных 3-деревьев и хордальных максимальных планарных графов высказал без доказательства Патил (Patil 1986). Для доказательства смотри статью Маркензона, Джустела и Пакиорника (Markenzon, Justel, Paciornik 2006). Для более общего описания хордальных планарных графов и эффективного алгоритма их распознавания смотрите статью Кумара и Мадхавана (Kumar, Madhavan 1989). Что любой хордальный полиэдральный граф является максимальным планарным, заметил Герлах (Gerlach 2004).
- Fowler, 1998.
- Факт, что графы Аполлония минимизируют число раскрасок с числом цветов большим четырёх был показан Биркгофом в двойственной форме раскраски карт (Birkhoff 1930).
- Felsner, Zickfeld, 2008.
- Bernardi, Bonichon, 2009.
- Два запрещённых минора для планарных графов даёт теорема Вагнера. О запрещённых минорах частичных 3-деревьев (которые включают также непланарный граф Вагнера) смотрите статьи Арнборга, Проскуровски, Корниела (Arnborg, Proskurowski, Corniel 1986) и Бодлаендера (Bodlaender 1998). Прямое доказательство того, что граф октаэдра и пятиугольной призмы являются единственными двумя планарными запрещёнными минорами, смотрите статьи Даи, Сато (Dai, Sato 1990) и Эль-Маллаха, Колбоурна (El-Mallah, Colbourn 1990).
- Политоф (Politof 1983) ввёл сводимые Δ-Y планарные графы и описал их в терминах запрещённых гомеоморфных подграфов. Двойственность между Δ-Y и Y-Δ сводимыми графами, описание обоих классов запрещёнными минорами и связь с планарными частичными 3-деревьями взяты из статьи Эль-Маллаха и Колбоурна (El-Mallah, Colbourn 1990).
- Для описания в терминах максимального числа треугольников в планарном графе смотрите статью Хакими и Шмейхеля (Hakimi, Schmeichel 1979). Алон и Саро цитируют этот результат и показывают описание в терминах изоморфизма классов блоков и числа блоков (Alon, Caro 1984). Граница общего числа клик довольно просто следует из границы числа теугольних подграфов и подграфов K4 и приведена в явном виде у Вуда (Wood 2007), который использовал графы Аполлония в качестве примера, показывающего строгость границы. Обобщение этих границ для непланарных поверхностей смотрите статью Дуймовича, Фиявжа, Жоре и Вуда (Dujmović, Fijavž, Joret, Wood 2009).
- Andrade, Herrmann, Andrade, da Silva, 2005.
- Thurston, 1978–1981.
- См., например, статью Белова, Де Лоэра и Рихтер-Геберта (Below, De Loera, Richter-Gebert 2000)
- Demaine, Schulz, 2011.
- Elcock, Gargantini, Walsh, 1987.
- Biedl, Ruiz Velázquez, 2010.
- Для деления треугольника с рациональными длинами сторон так, чтобы полученные треугольники тоже имели рациональные стороны, смотри статью Альмеринга (Almering 1963). Относительно общей проблемы поиска планарного графа с рациональными длинами сторон смотри статью Гилена, Гуо и Маккиннона (Geelen, Guo, McKinnon 2008).
- Для рисования с целыми координатами смотри стать. Мондала, Нишата, Рахмана и Алама (Mondal, Nishat, Rahman, Alam 2010). Для рисования на заданном множестве вершин смотри статью Нишата, Мондала и Рахмана (Nishat, Mondal, Rahman 2011).
- Plummer, 1992.
- Petersen, 1891.
- Jiménez, Kiwi, 2010.
- Tsourakakis, 2011.
- Zhou, Yan, Zhou, Fu, Wang, 2004.
- Zhou, Yan, Wang, 2005.
- Frieze, Tsourakakis, 2011.
- Albenque, Marckert, 2008.
- Zhang, Chen, Zhou, Fang, 2008.
- Butler, Graham, 2010.
- Takeo, 1960.
- См. статью Нишизеки (Nishizeki 1980) с примером негамильтонов графа, имеющего жёсткость 1 и статью Бёме, Харанта и Ткача (Böhme, Harant, Tkáč 1999) с доказательством, что графы Аполлония с большей жёсткостью являются гамильтоновыми. См. статью Герлаха (Gerlach 2004) с обобщением этого результата на более широкий класс планарных графов.
- Birkhoff, 1930.
- Grünbaum, 1963.
- Moon, Moser, 1963.
- Robertson, Seymour, 1984.
- Hakimi, Schmeichel, 1979.
- Alon, Caro, 1984.
- Patil, 1986.
- Grünbaum, 1967.
- Zickfeld, Ziegler, 2006.
- Badent, Binucci, Di Giacomo, Didimo, 2007.
Литература
- Marie Albenque, Jean-François Marckert. Some families of increasing planar maps // Electronic Journal of Probability. — 2008. — Т. 13. — С. 1624–1671. — doi:10.1214/ejp.v13-563. — arXiv:0712.0593.
- Almering. Rational quadrilaterals // Indagationes Mathematicae. — 1963. — Т. 25. — С. 192–199..
- N.Alon, Y. Caro. Convexity and Graph Theory: proceedings of the Conference on Convexity and Graph Theory, Israel, March 1981 / M. Rosenfeld, J. Zaks. — Elsevier, 1984. — С. 25–36. — (Annals of Discrete Mathematics 20, North-Holland Mathematical Studies 87). — ISBN 978-0-444-86571-7.
- José S. Andrade (Jr), Hans J. Herrmann, Roberto F. S. Andrade, Luciano R. da Silva. Apollonian Networks: Simultaneously Scale-Free, Small World, Euclidean, Space Filling, and with Matching Graphs // Physical Review Letters. — 2005. — Т. 94. — С. 018702. — doi:10.1103/physrevlett.94.018702. — arXiv:cond-mat/0406295.
- S. Arnborg, A. Proskurowski, D. Corniel. Forbidden Minors Characterization of Partial 3-trees. — Dept. of Computer and Information Science, University of Oregon, 1986. — (Technical Report CIS-TR-86-07).. Как процитировано в статье Эль-Маллаха и Колбоурна (El-Mallah, Colbourn 1990).
- Melanie Badent, Carla Binucci, Emilio Di Giacomo, Walter Didimo, Stefan Felsner, Francesco Giordano, Jan Kratochvíl, Pietro Palladino, Maurizio Patrignani, Francesco Trotta. Canadian Conference on Computational Geometry. — 2007.
- Alexander Below, Jesús A. De Loera, Jürgen Richter-Gebert. The Complexity of Finding Small Triangulations of Convex 3-Polytopes. — 2000.
- Olivier Bernardi, Nicolas Bonichon. Intervals in Catalan lattices and realizers of triangulations // Journal of Combinatorial Theory. — 2009. — Т. 116, вып. 1. — С. 55–75. — doi:10.1016/j.jcta.2008.05.005.
- Therese Biedl, Lesvia Elena Ruiz Velázquez. Graph Drawing, 17th International Symposium, GD 2009, Chicago, IL, USA, September 22–25, 2009, Revised Papers. — Springer-Verlag, 2010. — Т. 5849. — С. 316–322. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-11805-0_30.
- George D. Birkhoff. On the number of ways of colouring a map // Proceedings of the Edinburgh Mathematical Society. — 1930. — Т. 2. — С. 83–91. — doi:10.1017/S0013091500007598.
- Hans L. Bodlaender. A partial k-arboretum of graphs with bounded treewidth // Theoretical Computer Science. — 1998. — Т. 209, вып. 1–2. — С. 1–45. — doi:10.1016/S0304-3975(97)00228-4.
- Thomas Böhme, Jochen Harant, Michal Tkáč. More than one tough chordal planar graphs are Hamiltonian // Journal of Graph Theory. — 1999. — Т. 32, вып. 4. — С. 405–410. — doi:10.1002/(SICI)1097-0118(199912)32:4<405::AID-JGT8>3.3.CO;2-Q.
- S. Butler, Ron Graham. Fete of Combinatorics and Computer Science / G. Katona, A. Schrijver, T. Szonyi. — Heidelberg: Springer-Verlag, 2010. — Т. 29. — С. 23–42. — (Bolyai Society Mathematical Studies).
- Wayne Wei-Ming Dai, Masao Sato. IEEE International Symposium on Circuits and Systems. — 1990. — Т. 4. — С. 2677–2681. — doi:10.1109/ISCAS.1990.112560.
- Erik Demaine, André Schulz. Proc. ACM-SIAM Symposium on Discrete Algorithms. — 2011. — С. 1177–1187.
- Vida Dujmović, Gašper Fijavž, Gwenaël Joret, David R. Wood. The maximum number of cliques in a graph embedded in a surface. — 2009. — arXiv:0906.4142.
- Ehab S. El-Mallah, Charles J. Colbourn. On two dual classes of planar graphs // Discrete Mathematics. — 1990. — Т. 80, вып. 1. — С. 21–40. — doi:10.1016/0012-365X(90)90293-Q.
- E. W. Elcock, I. Gargantini, T. R. Walsh. Triangular decomposition // Image and Vision Computing. — 1987. — Т. 5, вып. 3. — С. 225–231. — doi:10.1016/0262-8856(87)90053-9.
- Stefan Felsner, Florian Zickfeld. On the number of planar orientations with prescribed degrees // Electronic Journal of Combinatorics. — 2008. — Т. 15, вып. 1. — С. R77. — arXiv:math/0701771.
- Alan M. Frieze, Charalampos E. Tsourakakis. High Degree Vertices, Eigenvalues and Diameter of Random Apollonian Networks. — 2011.
- Thomas Fowler. Unique Coloring of Planar Graphs. — Georgia Institute of Technology Mathematics Department, 1998. — (Ph.D. thesis).
- Jim Geelen, Anjie Guo, David McKinnon. Straight line embeddings of cubic planar graphs with integer edge lengths // Journal of Graph Theory. — 2008. — Т. 58, вып. 3. — С. 270–274. — doi:10.1002/jgt.20304.
- T. Gerlach. Toughness and Hamiltonicity of a class of planar graphs // Discrete Mathematics. — 2004. — Т. 286, вып. 1—2. — С. 61–65. — doi:10.1016/j.disc.2003.11.046.
- A. Goldner, F. Harary. Note on a smallest nonhamiltonian maximal planar graph // Bull. Malaysian Math. Soc.. — 1975. — Т. 6, вып. 1. — С. 41–42.. См. также журналы 6(2):33 (1975) и 8:104-106 (1977). Ссылки взяты из статьи Список публикаций Харари.
- Branko Grünbaum. Unambiguous polyhedral graphs // Israel Journal of Mathematics. — 1963. — Т. 1, вып. 4. — С. 235–238. — doi:10.1007/BF02759726.
- Branko Grünbaum. Convex Polytopes. — Wiley Interscience, 1967.
- S. L. Hakimi, E. F. Schmeichel. On the number of cycles of length k in a maximal planar graph // Journal of Graph Theory. — 1979. — Т. 3, вып. 1. — С. 69–86. — doi:10.1002/jgt.3190030108.
- Andrea Jiménez, Marcos Kiwi. Counting perfect matchings of cubic graphs in the geometric dual. — 2010. — arXiv:1010.5918.
- P. Sreenivasa Kumar, C. E. Veni Madhavan. Foundations of Software Technology and Theoretical Computer Science, Ninth Conference, Bangalore, India December 19–21, 1989, Proceedings. — Springer-Verlag, 1989. — Т. 405. — С. 30–43. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-52048-1_30.
- L. Markenzon, C. M. Justel, N. Paciornik. Subclasses of k-trees: Characterization and recognition // Discrete Applied Mathematics. — 2006. — Т. 154, вып. 5. — С. 818–825. — doi:10.1016/j.dam.2005.05.021.
- Debajyoti Mondal, Rahnuma Islam Nishat, Md. Saidur Rahman, Muhammad Jawaherul Alam. Canadian Conference on Computational Geometry. — 2010.
- J. W. Moon, L. Moser. Simple paths on polyhedra // Pacific Journal of Mathematics. — 1963. — Т. 13. — С. 629–631. — doi:10.2140/pjm.1963.13.629.
- Rahnuma Islam Nishat, Debajyoti Mondal, Md. Saidur Rahman. Graph Drawing, 18th International Symposium, GD 2010, Konstanz, Germany, September 21–24, 2010, Revised Selected Papers. — Springer-Verlag, 2011. — Т. 6502. — С. 317–328. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-18469-7_29.
- Takao Nishizeki. A 1-tough non-Hamiltonian maximal planar graph // Discrete Mathematics. — 1980. — Т. 30, вып. 3. — С. 305–307. — doi:10.1016/0012-365X(80)90240-X.
- H. P. Patil. On the structure of k-trees // Journal of Combinatorics, Information and System Sciences. — 1986. — Т. 11, вып. 2—4. — С. 57–64.
- Julius Petersen. Die Theorie der regulären graphs // Acta Mathematica. — 1891. — Т. 15. — С. 193–220. — doi:10.1007/BF02392606.
- Michael D. Plummer. Extending matchings in planar graphs IV // Discrete Mathematics. — 1992. — Т. 109, вып. 1–3. — С. 207–219. — doi:10.1016/0012-365X(92)90292-N.
- T. Politof. A characterization and efficient reliability computation of Δ-Y reducible networks. — University of California, Berkeley, 1983. — (Ph.D. thesis).. Как процитировано в статье Эль-Маллаха и Колбоурна El-Mallah, Colbourn (1990).
- Neil Robertson, P. D. Seymour. Graph minors. III. Planar tree-width // Journal of Combinatorial Theory. — 1984. — Т. 36, вып. 1. — С. 49–64. — doi:10.1016/0095-8956(84)90013-3.
- Fujio Takeo. On triangulated graphs. I // Bull. Fukuoka Gakugei Univ. III. — 1960. — Т. 10. — С. 9–21.. На ошибку относительно гамильтоновости в MathSciNet указал Уильям Татт.
- William Thurston. The geometry and topology of 3-manifolds. — Princeton lecture notes, 1978–1981.
- Charalampos E. Tsourakakis. The Degree Sequence of Random Apollonian Networks. — Department of Mathematical Sciences, Carnegie Mellon University, 2011. — arXiv:1106.1940v1.
- David R. Wood. On the maximum number of cliques in a graph // Graphs and Combinatorics. — 2007. — Т. 23, вып. 3. — С. 337–352. — doi:10.1007/s00373-007-0738-8. — arXiv:math/0602191.
- Zhongzhi Zhang, Lichao Chen, Shuigeng Zhou, Lujun Fang, Jihong Guan, Tao Zou. Analytical solution of average path length for Apollonian networks // Physical Review E. — 2008. — Т. 77. — С. 017102. — doi:10.1103/PhysRevE.77.017102. — arXiv:0706.3491.
- Tao Zhou, Gang Yan, Bing-Hong Wang. Maximal planar networks with large clustering coefficient and power-law degree distribution // Physical Review E. — 2005. — Т. 71, вып. 4. — С. 046141. — doi:10.1103/PhysRevE.71.046141. — arXiv:cond-mat/0412448.
- Tao Zhou, Gang Yan, Pei-Ling Zhou, Zhong-Qian Fu, Bing-Hong Wang. Random Apollonian networks. — University of Science and Technology of China, Hefei Anhui, 2004. — arXiv:cond-mat/0409414v2.
- Florian Zickfeld, Günter M. Ziegler. Workshop on Geometric and Topological Combinatorics. — Alcal ́a de Henares, Madrid, 2006.
Ссылки
- Weisstein, Eric W. Apollonian Network (англ.) на сайте Wolfram MathWorld.
- Matlab Simulation Code