Жёсткость графа

Жёсткость графа — мера связности графа: граф G t-жёсток при некотором вещественном t, если для любого целого k > 1 нельзя разбить граф G на k различных компонент связности путём удаления менее чем tk вершин. Например, граф 1-жёсток, если число компонент, образующихся при удалении вершин, всегда не превосходит числа удалённых вершин. Жёсткость графа — это максимальное t, для которого он t-жёсток. Число является конечным числом для всех конечных графов, за исключением полных графов, которые, по соглашению, имеют бесконечную жёсткость.

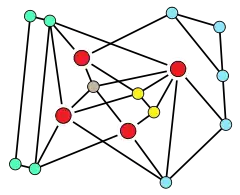
В этом графе удаление четырёх красных вершин даёт четыре связные компоненты (отражены четырьмя различными цветами). Однако не существует множества из k вершин, удаление которого оставляет более k компонент. Таким образом, жёсткость графа равна в точности 1.

Жёсткость была введена Вацлавом Хваталом в 1973 году[1]; впоследствии понятию было посвящено много обширных исследований других специалистов по теории графов, так, обзор 2006 года[2], целиком посвящённый жёсткости, насчитывает 99 теорем и 162 страницы.

Примеры

Удаление k вершин из графа-пути может разбить граф на k + 1 связных компонент. Максимальное отношение компонент к числу удаляемых вершин достигается удалением одной вершины (внутри пути), что приводит к разбиению пути на две компоненты. Таким образом, пути являются 1⁄2-жёсткими. Для контраста удаление k вершин из графа-цикла оставляет максимум k связных компонент, а иногда оставляет ровно k связных компонент, так что цикл является 1-жёстким.

Связь с вершинной связностью

Если граф t-жёсток, то получаем следствие (если положить k = 2), что любое множество из 2t − 1 вершин может быть удалено, но граф при этом не распадается на две части. То есть любой t-жёсткий граф является вершинно 2t-связным.

Связь с гамильтоновостью

Хватал[1] заметил, что любой цикл, а потому любой гамильтонов граф, является 1-жёстким. То есть 1-жёскость является необходимым условием, чтобы он был гамильтоновым. Хватал высказал предположение, что связь между жёсткостью и гамильтоновостью действует в обоих направлениях, то есть существует порог t, такой, что любой t-жёсткий граф является гамильтоновым. Начальная гипотеза Хватала, что t = 2 доказывала бы теорему Фляйшнера, но гипотезу опровергли Бауэр, Брёрсма и Вельдман[3]. Существование порога для гамильтоновости остаётся открытой проблемой.

Вычислительная сложность

Проверка, является ли граф 1-жёстким, есть co-NP-полная задача. То есть задача разрешимости, для которой ответ «да» означает, что граф не 1-жёсток, а ответ «нет» означает, что граф 1-жёсток, является NP-полной задачей. То же самое верно для любого фиксированного положительного рационального числа q — проверка, является ли граф q-жёстким, есть co-NP-полная задача[4].

См. также

Примечания
  1. Chvátal, 1973, с. 215–228.
  2. Bauer, Broersma, Schmeichel, 2006, с. 1–35.
  3. Bauer, Broersma, Veldman, 2000, с. 317–321.
  4. Bauer, Hakimi, Schmeichel, 1990, с. 191–195.

Литература
  • Douglas Bauer, Hajo Broersma, Edward Schmeichel. Toughness in graphs—a survey (англ.) // Graphs and Combinatorics. — 2006. — Vol. 22, iss. 1. — doi:10.1007/s00373-006-0649-0.
  • D. Bauer, H. J. Broersma, H. J. Veldman. Not every 2-tough graph is Hamiltonian (англ.) // Discrete Applied Mathematics. — 2000. — Vol. 99, iss. 1—3. — doi:10.1016/S0166-218X(99)00141-9.
  • D. Bauer, S. L. Hakimi, E. Schmeichel. Recognizing tough graphs is NP-hard (англ.) // Discrete Applied Mathematics. — 1990. — Vol. 28, iss. 3. — doi:10.1016/0166-218X(90)90001-S.
  • Václav Chvátal. Tough graphs and Hamiltonian circuits (англ.) // Discrete Mathematics. — 1973. — Vol. 5, iss. 3. — doi:10.1016/0012-365X(73)90138-6.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.