Теорема Фляйшнера

Теорема Фляйшнера — утверждение в теории графов, дающее достаточное условие, чтобы граф содержал гамильтонов цикл: если граф является вершинно 2-связным графом, то квадрат графа гамильтонов. Названа именем Герберта Фляйшнера, опубликовавшего доказательство теоремы в 1974 году.

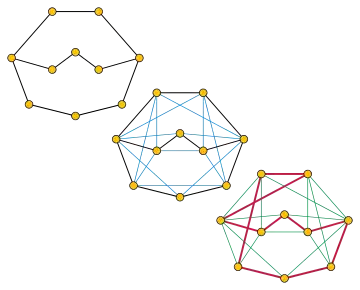
Вершинно 2-связный граф, его квадрат и гамильтонов цикл в квадрате

Определения и утверждение

Неориентированный граф G является гамильтоновым, если он содержит цикл, который проходит через каждую вершину в точности один раз. Граф является вершинно 2-связным, если он не содержит сочленяющих вершин, то есть вершин, удаление которых делает оставшийся граф несвязным. Не любой вершинно 2-связный граф является гамильтоновым. Контрпримеры включают граф Петерсена и полный двудольный граф K2,3.

Квадрат графа G — это граф G2, имеющий то же самое множество вершин, что и граф G, и в котором две вершины смежны тогда и только тогда, когда расстояние между ними в G не превосходит числа два. Теорема Фляйшера утверждает, что квадрат конечного вершинно 2-связного графа с тремя и более вершинами должен всегда быть гамильтоновым. Эквивалентно, вершины любого вершинно 2-связного графа G могут быть организованы в циклический порядок, так что смежные вершины в этом порядке в графе G находятся друг от друга на расстоянии, не превосходящем двух.

Расширения

В теореме Фляйшнера можно наложить ограничение на гамильтонов цикл так, чтобы он включал три выбранных ребра, проходящие через две выбранные вершины[1][2].

Кроме содержания гамильтонова цикла, квадрат вершинно 2-связного графа G должен быть также гамильтоново связан (что означает, что он имеет гамильтонов путь, начинающийся и заканчивающийся в любых двух выбранных вершинах) и 1-гамильтонов (что означает, что если удалить любую вершину, оставшийся граф также будет содержать гамильтонов цикл)[3][4]. Граф должен быть также вершинно панциклическим, что означает, что для любой вершины v и любого целого k с 3 ≤ k ≤ |V(G)| существует цикл длины k, содержащий v[5].

Если граф G не вершинно 2-связен, его квадрат может иметь, а может и не иметь гамильтонов цикл и определение, имеет ли граф такой цикл, является NP-полной задачей[6][7].

Бесконечный граф не может иметь гамильтонов цикл, поскольку любой цикл конечен, но Карстен Томассен доказали, что в случае, когда G является бесконечным локально конечным вершинно 2-связным графом с единым концом, то G2 обязательно имеет дважды бесконечный гамильтонов путь[8]. Более обще, если G локально конечен, вершинно 2-связен и имеет любое число концов, то G2 имеет гамильтонов цикл. В компактном топологическом пространстве, образованный рассмотрением графа как симплициальный комплекс и добавлением дополнительной точки на бесконечности для каждого конца графа, гамильтонов цикл определяется как подпространство, которое гомеоморфно евклидовой окружности и покрывает все вершины[9][10].

История

О доказательстве теоремы Герберт Фляшнер объявил в 1971 году и опубликовал в 1974 году, решив тем самым гипотезу 1966 года Нэш-Вильямса, которую независимо высказали также Л.У. Байник и Пламмер[11]. В своём обозрении статья Фляйшнера Нэш-Вильямс пишет, что тот решил «хорошо известную проблему, о которую несколько лет разбивалась изобретательность других теоретиков теории графов»[12].

Оригинальное доказательство Фляйшера было сложно. Вацлав Хватал в работе, в которой он ввёл понятие жёсткости графа, заметил, что квадрат вершинно k-связного графа обязательно k-жёсток. Он высказал предположение, что 2-жёсткие графы являются гамильтоновыми, из чего получилось бы другое доказательство теоремы Фляйшера[13][7]. Позднее были обнаружены контрпримеры этой гипотезе[14], но возможность, что из конечной границы жёсткости могла бы следовать гамильтоновость, осталась важной открытой проблемой в теории графов. Более простое доказательство как теоремы Флейшнера, так и её расширения, сделанные Чартрандом, Хоббсом, Янгом и Капууром[3], было дано Риха[15][7][4], а ещё одно упрощённое доказательство теоремы дал Георгакопулус[16][4][10].

Примечания
  1. Fleischner, 1976, с. 125–149.
  2. Müttel, Rautenbach, 2012.
  3. Chartrand, Hobbs, Jung, Kapoor, 1974.
  4. Chartrand, Lesniak, Zhang, 2010.
  5. Хоббс (Hobbs (1976)), ответ на гипотезу Бонди (Bondy, 1971).
  6. Underground, 1978.
  7. Bondy, 1995.
  8. Thomassen (1978).
  9. Georgakopoulos, 2009b.
  10. Diestel, 2012.
  11. Fleischner (1974). О более ранних гипотезах см. У Фляйшнера и Чартранда, Лесниака и Чжана (Chartrand, Lesniak, Zhang (2010)).
  12. MR: 0332573.
  13. Chvátal, 1973.
  14. Bauer, Broersma, Veldman, 2000.
  15. Říha, 1991.
  16. Georgakopoulos, 2009a.

Литература
  • D. Bauer, H. J. Broersma, H. J. Veldman. Proceedings of the 5th Twente Workshop on Graphs and Combinatorial Optimization (Enschede, 1997) (англ.) // Discrete Applied Mathematics. — 2000. — Vol. 99, no. 1—3. — P. 317–321. — doi:10.1016/S0166-218X(99)00141-9.
  • J. A. Bondy. Proceedings of the Second Louisiana Conference on Combinatorics, Graph Theory and Computing (Louisiana State Univ., Baton Rouge, La., 1971) (англ.). — Baton Rouge, Louisiana: Louisiana State University, 1971. — P. 167–172.
  • G. Chartrand, Arthur M. Hobbs, H. A. Jung, S. F. Kapoor, C. St. J. A. Nash-Williams. The square of a block is Hamiltonian connected (англ.) // Journal of Combinatorial Theory. — 1974. — Vol. 16. — P. 290–292. — doi:10.1016/0095-8956(74)90075-6.
  • Václav Chvátal. Tough graphs and Hamiltonian circuits (англ.) // Discrete Mathematics. — 1973. — Vol. 5, iss. 3. — P. 215–228. — doi:10.1016/0012-365X(73)90138-6.
  • Herbert Fleischner. The square of every two-connected graph is Hamiltonian (англ.) // Journal of Combinatorial Theory. — 1974. — Vol. 16. — doi:10.1016/0095-8956(74)90091-4.
  • H. Fleischner. In the square of graphs, Hamiltonicity and pancyclicity, Hamiltonian connectedness and panconnectedness are equivalent concepts (англ.) // Monatshefte für Mathematik. — 1976. — Vol. 82, iss. 2. — doi:10.1007/BF01305995.
  • Agelos Georgakopoulos. A short proof of Fleischner's theorem (англ.) // Discrete Mathematics. — 2009a. — Vol. 309, iss. 23—24. — P. 6632–6634. — doi:10.1016/j.disc.2009.06.024.
  • Agelos Georgakopoulos. Infinite Hamilton cycles in squares of locally finite graphs (англ.) // Advances in Mathematics. — 2009b. — Vol. 220, iss. 3. — P. 670–705. — doi:10.1016/j.aim.2008.09.014.
  • Arthur M. Hobbs. The square of a block is vertex pancyclic (англ.) // Journal of Combinatorial Theory. — 1976. — Vol. 20, iss. 1. — P. 1–4. — doi:10.1016/0095-8956(76)90061-7.
  • Janina Müttel, Dieter Rautenbach. A short proof of the versatile version of Fleischner’s theorem (англ.) // Discrete Mathematics. — 2012. — doi:10.1016/j.disc.2012.07.032.
  • Stanislav Říha. A new proof of the theorem by Fleischner (англ.) // Journal of Combinatorial Theory. — 1991. — Vol. 52, iss. 1. — P. 117–123. — doi:10.1016/0095-8956(91)90098-5.
  • Carsten Thomassen. Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977) (англ.) / B. Bollobás. — Elsevier, 1978. — Vol. 3. — P. 269–277. — (Annals of Discrete Mathematics). — ISBN 978-0-7204-0843-0. — doi:10.1016/S0167-5060(08)70512-0.
  • Paris Underground. On graphs with Hamiltonian squares (англ.) // Discrete Mathematics. — 1978. — Vol. 21, iss. 3. — P. 323. — doi:10.1016/0012-365X(78)90164-4.
  • J. A. Bondy. Handbook of combinatorics, Vol. 1, 2 (англ.). — Amsterdam: Elsevier, 1995. — P. 3–110.
  • Gary Chartrand, Linda Lesniak, Ping Zhang. Graphs & Digraphs (англ.). — 5th. — CRC Press, 2010. — P. 139. — ISBN 9781439826270.
  • Reinhard Diestel. Graph Theory (англ.). — corrected 4th electronic. — 2012.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.