Панциклический граф

Граф ${\displaystyle G}$ с ${\displaystyle n}$ вершинами является панциклическим, если для любого ${\displaystyle k}$ в пределах ${\displaystyle 3\leqslant k\leqslant n}$ граф ${\displaystyle G}$ содержит цикл длины ${\displaystyle k}$[1]. Граф является вершинно панциклическим, если для любой вершины ${\displaystyle v}$ и любого ${\displaystyle k}$ в тех же пределах граф содержит цикл длины ${\displaystyle k}$, содержащий вершину ${\displaystyle v}$[2]. Похожим образом граф является рёберно панциклическим, если для любого ребра ${\displaystyle e}$ и для любого ${\displaystyle k}$ в тех же пределах он содержит цикл длины ${\displaystyle v}$, содержащий ребро ${\displaystyle e}$[2].

Двудольный граф не может быть панциклическим, поскольку он не содержит циклы любой нечётной длины, но говорят, что граф является бипанциклическим, если он содержит циклы всех чётных длин от 4 до ${\displaystyle n}$[3].

Максимальный внешнепланарный граф — это граф, образованный из простого многоугольника на плоскости путём триагуляризации его внутренности. Любой максимальный внешнепланарный граф является панциклическим, что можно показать индукцией. Внешняя грань графа является циклом с n вершинами, а удаление любого треугольника, соединённого с остатком графа только одним ребром (лист дерева, которое образует двойственный граф триангуляризации), образует максимальный внешнепланарный граф с на единицу меньшим числом вершин, а по индукционному предположению этот граф имеет все циклы всех оставшихся длин. Если уделять больше внимания выбору треугольника для удаления, то те же аргументы показывают более строгий результат, что любой максимальный внешнепланарный граф является вершинно панциклическим[4]. То же самое верно для графов, которые имеют максимальный внешнепланарный граф в качестве остовного подграфа, в частности, для колёс.

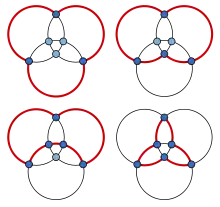
Максимальный планарный граф — это планарный граф, в котором все грани, включая внешнюю, являются треугольниками. Максимальный планарный граф является вершинно панциклическим тогда и только тогда, когда он содержит гамильтонов цикл[5] — если он не гамильтонов, он определённо не панцикличен, а если он гамильтонов, то внутренность гамильтонова цикла образует внешнюю грань максимального внешнепланарного графа на тех же вершинах и рёбрах, к которой можно применить предыдущие аргументы для внешнепланарных графов[6]. Например, на рисунке^{[каком?]} показана панцикличность графа октаэдра, гамильтонова максимального планарного графа с шестью вершинами. Более строго, по тем же самым причинам, если максимальный планарный граф имеет цикл длины ${\displaystyle k}$, он имеет циклы всех меньших длин[7].

Почти панциклический граф Халина с циклами всех длин вплоть до n, за исключением длины 8

Графы Халина являются планарными графами, образованными из планарного рисунка дерева, не имеющего вершин степени два, путём добавления цикла, соединяющего листья дерева. Графы Халина не обязательно панцикличны, но они почти панцикличны в том смысле, что отсутствует цикл максимум одной длины. Длина отсутствующего цикла обязательно чётна. Если ни одна из внутренних вершин графа Халина не имеет степень три, то граф обязательно панцикличен[8].

В 1971 году замечено[1], что много классических условий для существования гамильтонова цикла достаточны также для панцикличности, в связи с чем предположено, что любой 4-связный планарный граф панцикличен, но вскоре было найдено семейство контпримеров[9].

Турнир — это направленный граф с одной направленной дугой между любой парой вершин. Интуитивно турнир может быть использован для моделирования круговой системы путём рисования дуги от победителя к побеждённому для каждой игры в соревновании. Турнир называется сильно связным или просто сильным тогда и только тогда, когда он не может быть разделён на два непустых подмножества ${\displaystyle L}$ и ${\displaystyle W}$ проигравших и выигравших, так что любой участник ${\displaystyle W}$ побеждает любого участника в ${\displaystyle L}$[10]. Любой сильный турнир является панциклическим[11] и вершинно панциклическим[12]. Если турнир регулярен (любой участник имеет то же число выигрышей и проигрышей, что и другие участники), то он является также рёберно панциклическим[13], однако сильные турниры с четырьмя вершинами не могут быть рёберно панциклическими.

Теорема Мантеля утверждает, что любой неориентированный граф с ${\displaystyle n}$ вершинами, имеющий по меньшей мере ${\displaystyle n^{2}/4}$ рёбер и не имеющий кратных рёбер и петель, либо содержит треугольник, либо он является полным двудольным графом ${\displaystyle K_{n/2,n/2}}$. Эту теорему можно усилить — любой неориентированный гамильтонов граф с не менее чем ${\displaystyle n^{2}/4}$ рёбрами либо панцикличен, либо это ${\displaystyle K_{n/2,n/2}}$[1].

Существуют гамильтоновы ориентированные графы с ${\displaystyle n}$ вершинами и с ${\displaystyle n(n+1)/2-3}$ дугами, не являющиеся панциклическими, но любой гамильтонов ориентированный граф по меньшей мере с ${\displaystyle n(n+1)/2-1}$ дугами панцикличен. Кроме того, строго связный граф с ${\displaystyle n}$ вершинами, в котором каждая вершина имеет степень, не меньшую ${\displaystyle n}$ (входящие и исходящие дуги считаются вместе), либо панцикличен, либо является полным двудольным графом[14].

Для любого графа ${\displaystyle G}$ его ${\displaystyle k}$-я степень графа ${\displaystyle G^{k}}$ определяется как граф на том же множестве вершин, имеющий ребро между любыми двумя вершинами, расстояние между которыми в ${\displaystyle G}$ не превосходит ${\displaystyle k}$. Если ${\displaystyle G}$ вершинно 2-связен, то по теореме Фляйшнера ${\displaystyle G^{2}}$ является гамильтоновым графом. Утверждение может быть усилено: граф обязательно будет вершинно панциклическим[15]. Более строго, если ${\displaystyle G^{2}}$ является гамильтоновым, он также и панцикличен[16].

Проверка графа на панцикличность является NP-полной задачей даже для специального случая 3-связных кубических графов. NP-полной задачей является также проверка графа на вершинную панцикличность даже для специального случая полиэдральных графов[17]. Также NP-полной задачей является проверка квадрата графа на гамильтоновость, а тем самым и проверка на панцикличность[18].

Панцикличность впервые исследовали Харари и Мозер в контексте турниров[19], а также Муун[20] и Алпач[13]. Понятие панцикличности получило название от Бонди, который расширил понятие для неориентированных графов[1].

• Weisstein, Eric W. Pancyclic Graph (англ.) на сайте Wolfram MathWorld.