Колесо (теория графов)

В теории графов колесом Wn называется граф с n вершинами (n ≥ 4), образованный соединением единственной вершины со всеми вершинами (n-1)-цикла. Числовое обозначение колёс в литературе не устоялось — некоторые авторы используют n для обозначения длины цикла, так что их Wn означает граф Wn+1 по определению выше[1]. Колесо может быть определено также, как 1-скелет (n-1)-угольной пирамиды.

Примеры графов-колёс
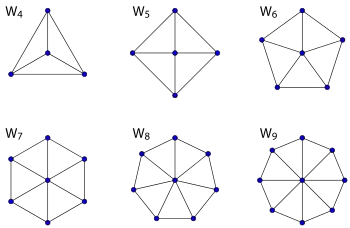Вершин n
Рёбер 2(n − 1)
Диаметр 2 при n>4
1 при n=4
Обхват 3
Хроматическое число 3 при нечётном n, 4 при чётном n
Свойства гамильтонов
двойственный
планарный
Обозначение Wn
 Медиафайлы на Викискладе

Представление в виде множества

Пусть задано множество вершин {1,2,3,…,v}. Множество рёбер графа-колеса можно представить в виде множества {{1,2},{1,3},…,{1,v},{2,3},{3,4},…,{v-1,v},{v,2}}[2].

Свойства

Колеса являются планарными графами, а потому имеют единственное вложение в плоскость. Любое колесо является графом Халина. Они самодвойственны — двойственный граф любого колеса изоморфен самому колесу. Любой максимальный планарный граф, отличный от K4 = W4, содержит в качестве подграфа либо W5, либо W6.

В колесе всегда имеется гамильтонов цикл и число циклов в Wn равно (последовательность A002061 в OEIS).


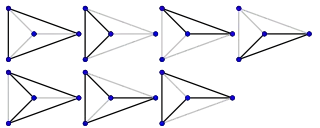7 циклов в колесе W4.

Для нечётных значений n Wn является совершенным графом с хроматическим числом 3 — вершины цикла можно выкрасить в два цвета, а центральная вершина будет иметь третий цвет. Для чётного n Wn колесо имеет хроматическое число 4 и (при n ≥ 6) не будет совершенным графом. W7 — это единственное колесо, являющееся графом единичных расстояний на евклидовой плоскости[3].

Хроматический многочлен колеса Wn равен:

В теории матроидов есть два особо важных вида матроидов — колеса и вихри, и оба вида являются производными от графов-колес. Матроид k-колёса — это графовый матроид колеса Wk+1, а матроид k-вихря получается из матроида k-колеса путём объявления внешнего цикла (обода) таким же независимым множеством, как и его остовные деревья.

Колесо W6 даёт контрпример гипотезе Пола Эрдёша в теории Рамсея — он высказал предположение, что полный граф имеет наименьшее число Рамсея среди всех графов с тем же хроматическим числом. Однако Фаудри и МакКей (Faudree, McKay, 1993) показали, что для W6 число Рамсея равно 17, в то время как для полного графа K4, с тем же хроматическим числом, число Рамсея равно 18[4]. Таким образом, для любого графа G с 17 вершинами либо сам G, либо его дополнение содержит W6 как подграф, в то время как ни граф Пэли, имеющий 17 вершин, ни его дополнение не содержат K4.

Примечания
  1. Weisstein, Eric W. Wheel Graph (англ.) на сайте Wolfram MathWorld.
  2. Richard J. Trudeau. Introduction to Graph Theory. — Corrected, enlarged republication. — New York: Dover Pub. — С. 56. — ISBN 978-0-486-67870-2.
  3. Fred Buckley, Frank Harary. On the euclidean dimension of a wheel // Graphs and Combinatorics. — 1988. — Т. 4, вып. 1. — С. 23–30. — doi:10.1007/BF01864150.
  4. Ralph J. Faudree, Brendan D. McKay. A conjecture of Erdős and the Ramsey number r(W6) // J. Combinatorial Math. and Combinatorial Comput. — 1993. — Т. 13. — С. 23–31.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.