Граф Пэли
В теории графов графами Пэли (названы в честь Раймонда Пэли) называются плотные неориентированные графы, построенные из членов подходящего конечного поля путём соединения пар элементов, отличающихся на квадратичный вычет. Графы Пэли образуют бесконечное семейство конференсных графов, поскольку тесно связаны с бесконечным семейством симметричных конференсных матриц. Графы Пэли дают возможность применить теоретические средства теории графов в теории квадратичных вычетов и имеют интересные свойства, что делает их полезными для теории графов в общем.
| Граф Пэли | |
|---|---|
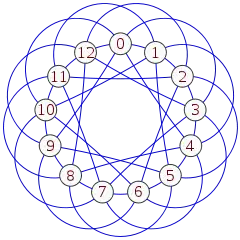 Граф Пэли 13-го порядка | |
| Вершин | q ≡ 1 mod 4, q — степень простого числа |
| Рёбер | q(q − 1)/4 |
| Свойства |
Сильно регулярный Самодополнительный Конференсный граф |
| Обозначение | QR(q) |
Графы Пэли тесно связаны с построением Палея для построения матриц Адамара из квадратичных вычетов (Пэли, 1933)[1]. Они были введены как графы независимо Саксом (Sachs, 1962) и Эрдёшем совместно с Реньи (Erdős, Rényi, 1963)[2]. Хорст Сакс (Horst Sachs) интересовался ими из-за их свойства самодополнительности, в то время как Эрдёш и Реньи изучали их симметрии.
Орграфы Пэли являются прямым аналогом графов Пэли и соответствуют антисимметричным конференсным матрицам. Они были введены Грэмом и Спенсером[3] (и, независимо, Саксом, Эрдёшем и Реньи) как путь построения турниров со свойствами, ранее известными только для случайных турниров: в орграфах Пэли любое подмножество вершин доминируется какой-либо вершиной.
Определение
Пусть q — степень простого числа, такая, что q = 1 (mod 4). Заметим, что отсюда вытекает существование квадратного корня из −1 в единственном конечном поле Fq , имеющем порядок q.
Пусть также V = Fq и
- .
Это множество корректно определено, поскольку a − b = −(b − a), и −1 является квадратом некоего числа, откуда следует, что a − b является квадратом тогда и только тогда, когда b − a является квадратом.
По определению G = (V, E) — граф Пэли порядка q.
Пример
Для q = 13 поле Fq образуется числами по модулю 13. Числа, имеющие квадратные корни по модулю 13:
- ±1 (квадратные корни ±1 для +1, ±5 для −1)
- ±3 (квадратные корни ±4 для +3, ±6 для −3)
- ±4 (квадратные корни ±2 для +4, ±3 для −4).
Таким образом, граф Пэли образуется вершинами, соответствующими числам из интервала [0,12], и каждая вершина x соединена с шестью соседями: x ± 1 (mod 13), x ± 3 (mod 13), и x ± 4 (mod 13).
Свойства
- Графы Пэли являются самодополнительным — дополнение любого графа Пэли изоморфно самому графу.[4]
- Эти графы сильно регулярны с параметрами
- Вдобавок графы Пэли, фактически, образуют бесконечное семейство конференсных графов.
- Собственные значения графов Пэли — это числа (с кратностью 1) и (оба с кратностью ) и могут быть вычислены с помощью квадратичных сумм Гаусса.
- Если q — простое, границами изопериметрического числа i(G) будут:
- Отсюда следует, что i(G)~O(q), и граф Пэли является экспандером.
- Если q — простое, его граф Пэли является гамильтоновым циклом циркулянтного графа.
- Графы Пэли квазислучайны (Чанг и др., 1989)[5] — число случаев, когда граф постоянного порядка окажется подграфом графа Пэли, равен (в пределе для больших q) тем же, что и для случайных графов, а при больших множествах вершин имеет примерно то же самое число рёбер, что и у случайных графов.
Приложения
- Граф Пэли 17-го порядка является единственным наибольшим графом G, таким, что ни он сам, ни его дополнение не содержат полный подграф с 4 вершинами (Эванс и др., 1981).[6] Из этого следует, что число Рамсея R(4, 4) = 18.
- Граф Пэли 101-го порядка пока единственный известный максимальный граф G, такой, что ни G, ни его дополнение не содержат полного подграфа с 6 вершинами.
- Сасакура[7] использовал графы Пэли для обобщения построения пучка Хоррокса-Мамфорда.
Орграфы Пэли
Пусть q — степень простого числа, такая, что q = 3 (mod 4). Тогда конечное поле Fq порядка q не имеет квадратного корня из −1. Следовательно, для любой пары (a,b) различных элементов Fq либо a − b, либо b − a, но не оба, являются квадратами. Орграф Пэли — это ориентированный граф с множеством вершин V = Fq и множеством дуг
Орграф Пэли является турниром, поскольку каждая пара различных вершин связана дугой в одном и только в одном направлении.
Орграф Пэли ведёт к построению некоторых антисимметричных конференсных матриц и двухплоскостной геометрии.
Род графа
Шесть соседей каждой вершины в графе Пэли 13-го порядка соединены в цикл, так что граф локально цикличен. Таким образом, этот граф может быть вложен в триангуляцию Уитни тора, в которой каждая грань является треугольником и каждый треугольник является гранью. В более общем случае, если какой-либо граф Пэли порядка q может быть вложен таким образом, что все его грани являются треугольниками, мы можем вычислить род результирующей поверхности с помощью эйлеровой характеристики . Мохар (Bojan Mohar, 2005) высказал гипотезу, что минимальный род поверхности, в которую может быть вложен граф Пэли, где-то около этого значения в случае, если q является квадратом, и поставил вопрос, можно ли обобщить такие границы. В частности, Мохар предположил, что графы Пэли квадратного порядка могут быть вложены в поверхности рода
где член o(1) может быть любой функцией от q, стремящейся к нулю при стремлении q к бесконечности.
Уайт (White, 2001) [8] нашёл вложение графов Пэли порядка q ≡ 1 (mod 8), обобщая естественное вложение графа Пэли 9-го порядка как квадратной решётки на тор. Однако род вложения Уитни выше примерно в три раза границы, которую Мохар высказал в своей гипотезе.
Ссылки
- R. E. A. C. Paley. On orthogonal matrices // J. Math. Phys.. — Т. 12. — С. 311–320.
- Asymmetric graphs // Acta Mathematica Academiae Scientiarum Hungaricae. — 1963. — Т. 14, вып. 3–4. — С. 295–315. — doi:10.1007/BF01895716.
- R. L. Graham, J. H. Spencer. A constructive solution to a tournament problem // Canadian Mathematical Bulletin. — 1971. — Т. 14. — С. 45–48. — doi:10.4153/CMB-1971-007-1.
- Horst Sachs. Über selbstkomplementäre Graphen // Publicationes Mathematicae Debrecen. — 1962. — Т. 9. — С. 270–288.
- Chung, Fan R. K., Р. Грэм, R. M. Wilson,. Quasi-random graps // Combinatorica. — 1989. — Т. 9, вып. 4. — С. 345–362. — doi:10.1007/BF02125347.
- Evans, R. J.; Pulham, J. R.; Sheehan, J. On the number of complete subgraphs contained in certain graphs // Journal of Combinatorial Theory, Series B. — 1981. — Т. 30, вып. 3. — С. 364–371. — doi:10.1016/0095-8956(81)90054-X.
- Sasakura, Nobuo; Enta, Yoichi; Kagesawa, Masataka. Construction of rank two reflexive sheaves with similar properties to the Horrocks–Mumford bundle // Proc. Japan Acad., Ser. A. — 1993. — Т. 69, вып. 5. — С. 144–148. — doi:10.2183/pjab.69.144.
- White, A. T. Graphs of groups on surfaces // Interactions and models. — Amsterdam: North-Holland Mathematics Studies 188, 2001.
- Baker, R. D.; Ebert, G. L.; Hemmeter, J.; Woldar, A. J. Maximal cliques in the Paley graphs of square order // J. Statist. Plann. Inference. — 1996. — Т. 56. — С. 33–38. — doi:10.1016/S0378-3758(96)00006-7.
- Broere, I.; Döman, D.; Ridley, J. N. The clique numbers and chromatic numbers of certain Paley graphs // Quaestiones Mathematicae. — 1988. — Т. 11. — С. 91–93. — doi:10.1080/16073606.1988.9631945.
Внешние ссылки
- Brouwer, Andries E. Paley graps (недоступная ссылка — история ). (недоступная ссылка)
- Mohar, Bojan. PaleyGenus.html Genus of Paley graps (2005). (недоступная ссылка)