Степень графа

Степень k (записывается Gk) неориентированного графа G — это другой граф, имеющий тот же самый набор вершин, и две вершины этого графа смежны, если расстояние между этими вершинами в исходном графе G не превышает k. Для указания степени графа используется терминология, аналогичная степеням чисел — G2 называется квадратом графа G, G3 называется кубом[1].

Квадрат графа

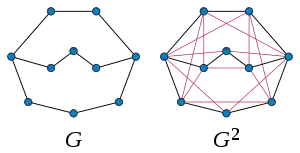
Степень графа не следует путать с умножением графа на себя, который (в отличие от степени графа), в общем случае, имеет много больше вершин, чем исходный граф.

Свойства

Если диаметр графа равен d, то его d-ая степень является полным графом[2]. Если семейство графов имеет ограниченную кликовую ширину, то это же верно и для d-х степеней графов семейства для любого фиксированного d[3].

Раскраска

Раскраску квадрата графа можно использовать для назначения частот участникам беспроволочной сети таким образом, чтобы никакие два участника не мешали бы друг другу и любому другому из общих соседей[4], а также для поиска графического представления графов с большим угловым разрешением[5].

Как хроматическое число, так и вырожденность k-ой степени планарного графа с максимальной степенью вершины Δ равны , где граница вырождения показывает, что можно использовать алгоритм жадной раскраски для раскраски графа таким числом цветов[4]. Для случая квадрата планарного графа Вегнер в 1977 году высказал гипотезу, что хроматическое число такого графа не превышает , и на текущий момент известно, что хроматическое число не превышает [6][7]. Более обще, для любого графа с вырождением d и максимальной степенью Δ вырождение квадрата графа равно O(dΔ), так что многие виды разреженных графов, отличные от планарных графов, также имеют пропорциональное Δ хроматическое число квадрата.

Хотя хроматическое число квадрата непланарного графа с максимальной степенью Δ может быть в худшем случае пропорционально Δ2, оно меньше для графов с большим обхватом и для этого случая ограничено числом O(Δ2/log Δ)[8].

Задача определения минимального числа цветов для раскраски квадратного графа NP-трудна даже для планарного случая[9]

Гамильтоновость

Куб любого связного графа обязательно содержит гамильтонов цикл[10]. Квадрат связного графа не обязательно будет содержать гамильтонов цикл и задача определения, что такой цикл содержится в квадрате, NP-полна[11]. Тем не менее, согласно теореме Фляйшнера, квадрат вершинно 2-связного графа всегда гамильтонов[12].

Вычислительная сложность

Степень k графа с n вершинами и m рёбрами можно получить за время O(mn) путём применения поиска в ширину, который осуществляется для каждой вершины графа с целью нахождения расстояний до всех других вершин. Альтернативно, если A — матрица смежности графа, модифицированная таким образом, что на главной диагонали не стоят нулевые элементы, то ненулевые элементы матрицы Ak дают матрицу смежности k-ой степени графа[13], откуда следует, что построение k-ой степени графа может быть осуществлено за время, равное, с точностью до логарифмического множителя, времени умножения матриц.

Если граф задан, определение, не является ли он квадратом другого графа, является NP-полной задачей[14]. Более того, NP-полной задачей является определение, является ли граф k-ой степенью другого графа для любого заданного числа k ≥ 2, а также является ли он k-ой степенью двудольнго графа для k > 2[15].

Порождённые подграфы
K4 как полуквадрат графа куба

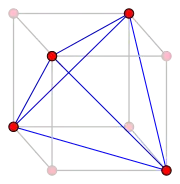
Полуквадрат двудольного графа G — это подграф графа G2, порождённый одной долей графа G. Графы карт — это полуквадраты планарных графов[16] , уполовиненные графы кубов — это полуквадраты графов гиперкубов[17].

Степени листьев — это подграфы степеней деревьев, порождённые листьями деревьев[18].

Примечания
  1. Bondy, Murty, 2008, с. 82.
  2. Weisstein, Eric W. Graph Power (англ.) на сайте Wolfram MathWorld.
  3. Todinca, 2003, с. 370–382.
  4. Agnarsson, Halldórsson, 2000, с. 654–662.
  5. Formann, Hagerup, Haralambides и др., 1993, с. 1035–1052.
  6. F. & H. Kramer, 2008, с. 422–426.
  7. Molloy, Salavatipour, 2005, с. 189–213.
  8. Alon, Mohar, 2002, с. 1–10.
  9. Агнаррссон и Халлдорссон (Agnarsson, Halldórsson 2000) перечислили в своей статье публикации доказательства NP-трудности для случая общих графов, (статьи Маккормика (McCormick, 1983) и статьи Лина и Скиена (Lin, Skiena, 1995)), и для планарных графов (статьи Раманатхана и Ллойда (Ramanathan, Lloyd, 1992-1993)).
  10. Bondy, Murty, 2008, с. 105.
  11. Underground, 1978, с. 323.
  12. Diestel, 2012.
  13. Hammack, Imrich, Klavžar, 2011.
  14. Motwani, Sudan, 1994, с. 81-88.
  15. Le, Nguyen, 2010, с. 238–249.
  16. Chen, Grigni, Papadimitriou, 2002, с. 127–138.
  17. Шпекторов, 1993.
  18. Nishimura, Ragde, Thilikos, 2002, с. 69–108.

Литература
  • Adrian Bondy, U. S. R. Murty. Graph Theory. — Springer, 2008. — Т. 244. — (Graduate Texts in Mathematics). — ISBN 9781846289699.
  • Ioan Todinca. Coloring powers of graphs of bounded clique-width // Graph-theoretic concepts in computer science. — Springer, Berlin, 2003. — Т. 2880. — (Lecture Notes in Comput. Sci.). — doi:10.1007/978-3-540-39890-5_32.
  • Geir Agnarsson, Magnús M. Halldórsson. Coloring powers of planar graphs // Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '00). — San Francisco, California, USA, 2000.
  • M. Formann, T. Hagerup, J. Haralambides, M. Kaufmann, F. T. Drawing graphs in the plane with high resolution // SIAM Journal on Computing. — 1993. — Т. 22, вып. 5. — doi:10.1137/0222063.
  • Florica Kramer, Horst Kramer. A survey on the distance-colouring of graphs // Discrete Mathematics. — 2008. — Т. 308, вып. 2-3. — doi:10.1016/j.disc.2006.11.059.
  • Michael Molloy, Mohammad R. Salavatipour. A bound on the chromatic number of the square of a planar graph // Journal of Combinatorial Theory. — 2005. — Т. 94, вып. 2. — doi:10.1016/j.jctb.2004.12.005.
  • Noga Alon, Bojan Mohar. The chromatic number of graph powers // Combinatorics, Probability and Computing. — 2002. — Т. 11, вып. 1. — doi:10.1017/S0963548301004965.
  • Polly Underground. On graphs with Hamiltonian squares // Discrete Mathematics. — 1978. — Т. 21, вып. 3. — doi:10.1016/0012-365X(78)90164-4.
  • Reinhard Diestel. 10. Hamiltonian cycles // Graph Theory. — 2012.
    • Рейнгард Дистель. Теория графов. — Новосибирск: Изд-во Ин-та математики, 2002. — ISBN 5-86134-101-X УДК 519.17 ББК 22.17.
  • Richard Hammack, Wilfried Imrich, Sandi Klavžar. Handbook of Product Graphs. — CRC Press, 2011. — (Discrete Mathematics and Its Applications). — ISBN 9781439813058.
  • R. Motwani, M. Sudan. Computing roots of graphs is hard // Discrete Applied Mathematics. — 1994. — Т. 54. — P. 81–88. — doi:10.1016/0166-218x(94)00023-9.
  • Van Bang Le, Ngoc Tuy Nguyen. Hardness results and efficient algorithms for graph powers // Graph-Theoretic Concepts in Computer Science: 35th International Workshop, WG 2009, Montpellier, France, June 24-26, 2009, Revised Papers. — Berlin: Springer, 2010. — Т. 5911. — (Lecture Notes in Computer Science). — ISBN 978-3-642-11408-3. — doi:10.1007/978-3-642-11409-0_21.
  • Zhi-Zhong Chen, Michelangelo Grigni, Christos H. Papadimitriou. Map graphs // Journal of the ACM. — 2002. — Т. 49, вып. 2. — doi:10.1145/506147.506148.
  • Shpectorov. On scale embeddings of graphs into hypercubes // European Journal of Combinatorics. — 1993. — Т. 14, вып. 2. — doi:10.1006/eujc.1993.1016.
  • N. Nishimura, P. Ragde, D.M. Thilikos. On graph powers for leaf-labeled trees // Journal of Algorithms. — 2002. — Т. 42. — doi:10.1006/jagm.2001.1195.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.