Огранка (геометрия)
В геометрии огранка — это процесс удаления части многоугольника или многогранника без создания новых вершин.
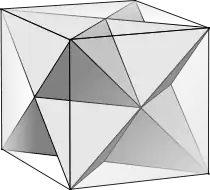
Звёздчатый октаэдр как огранка куба
Новые рёбра огранённого многогранника могут быть созданы вдоль диагоналей граней или внутренних диагоналей. Огранённый многогранник будет иметь две грани для каждого ребра и является новым многогранником или соединением многогранников.
Огранка является обратным или двойственным образованию звёздчатой формы. Для каждой звёздчатой формы некоторого выпуклого многогранника существует двойственная огранка двойственного многогранника.
Огранённые многоугольники
Например, правильный пятиугольник имеет одну симметричную огранку, пентаграммы, а правильный шестиугольник имеет две симметричные огранки, одна из них — многоугольник, а другая является соединением двух треугольников.
| Выпуклые | ||
|---|---|---|
| Правильный пятиугольник {5} |
Правильный шестиугольник {6} | |
 |
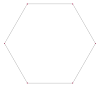 | |
| Правильные | Квазиправильные | Правильные соединения |
| Пентаграмма {5/2} |
Звёздчатый шестиугольник | гексаграмма {6/2} |
 |
 |
.svg.png.webp) |
Огранённые многогранники
Правильный икосаэдр может быть огранён до трёх правильных многогранников Кеплера — Пуансо — малого звёздчатого додекаэдра, большого додекаэдра и большого икосаэдра. Они имеют 30 рёбер.
| Выпуклые | Правильные звёзды | ||
|---|---|---|---|
| икосаэдр | Большой додекаэдр | Малый звёздчатый додекаэдр | Большой икосаэдр |
 |
 |
 |
 |
Правильный додекаэдр может быть огранён до одного правильного многогранника Кеплера — Пуансо, трёх однородных звёздчатых многогранников и трёх соединений многогранников. Однородные звёзды и соединение пяти кубов строятся на диагоналях граней. Выемчатый додекаэдр является огранкой со звёздчатыми октаграммными гранями.
| Выпуклые | Правильные звёзды | Однородные звёзды | Вершинно транзитивные | ||
|---|---|---|---|---|---|
| додекаэдр | большой звёздчатый додекаэдр | Малый битригональный икосододекаэдр | Битригональный додекаэдр | Большой битигональный икосододекаэдр | Выемчатый додекаэдр |
 |
 |
 |
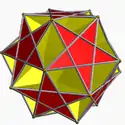 |
 |
 |
| Выпуклые | Правильные соединения | ||
|---|---|---|---|
| додекаэдр | пять тетраэдров | пять кубов | десять тетраэдров |
 |
 |
 |
 |
История
Огранка изучалась не столь интенсивно, как образование звёздчатой формы.
- В 1619 году Кеплер описал правильное соединение двух тетраэдров, заключённых в куб, которое назвал Stella octangula. Похоже, это первый известный пример огранки.
- В 1858 году Бертран получил правильные звёздчатые многогранники (тела Кеплера — Пуансо) путём огранки правильных выпуклых икосаэдра и додекаэдра.
- В 1974 году Бридж перечислил несколько огранок правильных многогранников, включая огранки додекаэдра.
- В 2006 году Инчибальд описал базовую теорию диаграмм огранки для многогранников. Для заданной вершины диаграмма показывает возможные рёбра и фасеты (новые грани), которые могут быть использованы для огранки исходной оболочки. Эта диаграмма двойственна диаграмме образования звёздчатой формы двойственного многогранника, которая показывает все возможные рёбра и вершины для некоторой плоскости грани исходного ядра.
Примечания
Литература
- J. Bertrand. Note sur la théorie des polyèdres réguliers // Comptes rendus des séances de l'Académie des Sciences. — 1858. — Т. 46. — С. 79—82.
- N. J. Bridge. Facetting the dodecahedron // Acta crystallographica. — 1974. — Т. A30. — С. 548—552.
- G. Inchbald. Facetting diagrams // The mathematical gazette. — 2006. — Т. 90. — С. 253—261.
- Alan Holden. Shapes, Space, and Symmetry. — New York: Dover, 1991. — Т. 94.