Метод Шульце
Метод Шульце (также метод последовательного исключения Шварца) — система голосования, разработанная в 1997 году Маркусом Шульце.
Сам Шульце называет её «методом разъезженного пути» (англ. beatpath method). Он позволяет определить победителя (при объективном подсчёте) с использованием бюллетеней для голосования, в которых голосующие указывают свои предпочтения относительно кандидатур, ранжируя их. Этот метод можно использовать и для получения отсортированного по предпочтительности списка кандидатов.
Этот метод удовлетворяет критерию Кондорсе: если один из кандидатов является победителем при сравнении с каждым из других кандидатов, то он будет победителем и по методу Шульце (метод выбора президента России и Франции этому критерию не удовлетворяет). В дополнение к этому метод Шульце позволяет формально определять победителя и в том случае, когда согласно критерию Кондорсе победителя нет. Победитель по методу Шульце всегда принадлежит множеству Шварца.
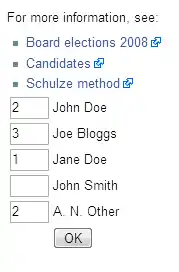
В методе Шульце каждый бюллетень содержит полный список кандидатов, и каждый избиратель ранжирует их в порядке своего предпочтения. В самом распространённом формате используются числа по возрастанию, когда избиратель ставит «1» напротив имени самого желательного кандидата, «2» — напротив второго по предпочтительности, и так далее. Избиратели могут ставить одинаковые числа нескольким кандидатурам, либо вообще не заполнять это поле для части кандидатур (в таком случае считается, что избиратель поставил такие кандидатуры одинаково ниже всех, для которых он указал число).
Существуют различные эвристики, позволяющие определять победителя голосования по таким исходным данным. На сегодняшний день наиболее употребительной является эвристика пути (англ. path heuristic) метода Шульце.
Эвристика пути
Основная идея эвристики пути — концепция косвенных побед, так называемых путей.
Если при парном сравнении кандидат C(1) побеждает C(2), кандидат C(2) побеждает C(3), кандидат C(3) побеждает C(4), …, и C(n − 1) побеждает C(n), то мы можем говорить, что существует путь от кандидата C(1) к кандидату C(n). Чем больше голосующих предпочитают первого кандидата второму кандидату, тем сильнее победа первого над вторым. Силой пути C(1), …, C(n) является слабейшая парная победа одного кандидата над другим в этой последовательности.
Другими словами:
- Предположим, что d[V, W] — число голосующих, которые строго предпочитают кандидатуру V кандидатуре W.
- Путь — это последовательность кандидатур C(1), …, C(n), где d[C(i), C(i + 1)] > d[C(i + 1), C(i)] для всех i = 1, …, n − 1.
- Сила пути C(1), …, C(n) — это минимум d[C(i), C(i + 1)] для всех i = 1, …, n − 1, где C(i) — позиция номер i с начала пути; d[A, B] — количество человек, поставивших кандидата A выше на одну или несколько позиций, чем кандидата B, при этом, если определён рассматриваемый путь, то имена кандидатов могут заменяться их позициями в данном пути.
Силой сильнейшего пути p[A, B] от кандидатуры A к кандидатуре B называется максимум значений силы всех возможных путей от кандидатуры A до кандидатуры B. Если пути от кандидатуры A к кандидатуре B не существует, то p[A, B] принимается равной нулю.
Кандидат A побеждает кандидата B косвенно, если выполняется любое из двух следующих условий:
- Сила сильнейшего пути от кандидата A к кандидату B сильнее, чем сила сильнейшего пути от кандидата B к кандидату A.
- Существует путь от кандидата A к кандидату B, а пути от кандидата B к кандидату A не существует.
Косвенные победы удовлетворяют условию транзитивности. Это означает, что если кандидат A косвенно побеждает кандидата B, а кандидат B косвенно побеждает кандидата C, то кандидат A также побеждает кандидата C косвенно.
Процедура
В эвристике пути используется следующая процедура построения графа путей предпочтения и определение силы путей:
Путём силы p от кандидата X до кандидата Y называется последовательность кандидатур C(1), …, C(n) со следующими пятью свойствами:
- C(1) принимается равным X.
- C(n) принимается равным Y.
- Для всех i от 1 до n − 1: d[C(i), C(i + 1)] > d[C(i + 1), C(i)].
- Для всех i от 1 до n − 1: d[C(i), C(i + 1)] ⩾ p.
- По крайней мере для одного i из диапазона от 1 до n − 1: d[C(i), C(i + 1)] = p, где p — сила пути от кандидата X до кандидата Y, то есть p[X, Y].
Кандидатура A является возможным победителем тогда и только тогда, когда p[A, Z] ⩾ p[Z, A] для каждой другой кандидатуры Z.
Пример 1
| d[*, A] | d[*, B] | d[*, C] | |
|---|---|---|---|
| d[A, *] | — | 70 | 33 |
| d[B, *] | 27 | — | 60 |
| d[C, *] | 64 | 37 | — |
Жирным выделены значения d[X, Y] > d[Y, X]. Как видно из таблицы, в этом примере каждому кандидату предпочитается другой кандидат — имеет место парадокс Кондорсе. Однако сила предпочтения различается. Предпочтение, отдаваемое кандидату A перед кандидатом B, больше предпочтения, отдаваемого кандидату C перед кандидатом A.
Кандидат A лучше кандидата B, который лучше кандидата С, который лучше кандидата A… Здесь нарушается транзитивность и нет победителя по критерию Кондорсе. Однако, для установления победителя в подобных случаях можно одну за другой отбрасывать самые слабые из сильных путей, в данном случае начав с d[C, A] = 64[прояснить], в результате чего победителем будет признан кандидат А[прояснить].
Пример 2
Рассмотрим выборы, на которых 45 избирателей голосуют за пять кандидатов: A, B, C, D, E. Голоса распределились следующим образом:
- 5 ACBED (то есть 5 избирателей поставили A выше C, C выше B, B выше E, а E выше D),
- 5 ADECB,
- 8 BEDAC,
- 3 CABED,
- 7 CAEBD,
- 2 CBADE,
- 7 DCEBA,
- 8 EBADC.
| d[*, A] | d[*, B] | d[*, C] | d[*, D] | d[*, E] | |
|---|---|---|---|---|---|
| d[A, *] | 20 | 26 | 30 | 22 | |
| d[B, *] | 25 | 16 | 33 | 18 | |
| d[C, *] | 19 | 29 | 17 | 24 | |
| d[D, *] | 15 | 12 | 28 | 14 | |
| d[E, *] | 23 | 27 | 21 | 31 |
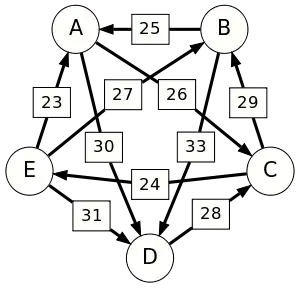
Сила пути — это сила его слабейшего звена (критическое звено). Пути, каждый переход в которых удовлетворяет d[X, Y] > d[Y, X] можно построить, пользуясь следующими кусочками последовательностей AC, AD, BA, BD, CB, CE, DC, EA, EB, ED.
Следующая таблица показывает сильнейшие пути от кандидата X к кандидату Y. Критическое звено сильнейшего пути подчёркнуто.
| … к A | … к B | … к C | … к D | … к E | |
|---|---|---|---|---|---|
| от A … | 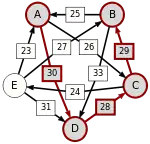 | 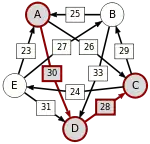 | 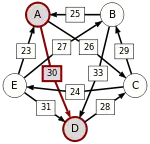 | 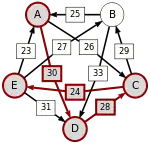 | |
| от B … | 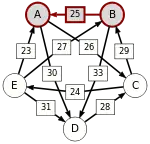 | 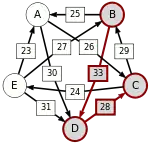 | 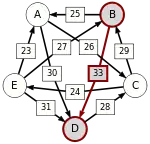 | 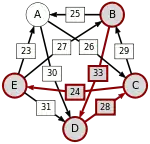 | |
| от C … | 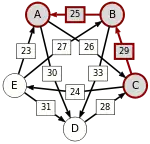 | 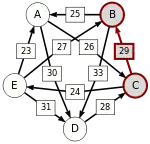 | 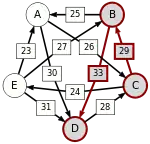 | 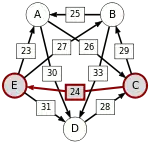 | |
| от D … | 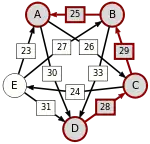 | 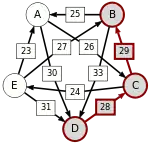 | 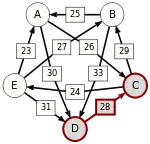 | 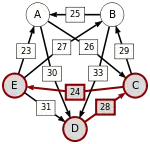 | |
| от E … | 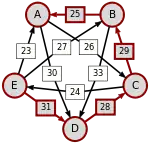 | 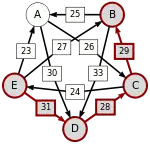 | 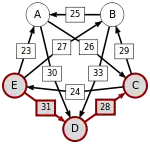 | 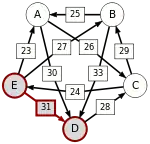 |
| p[*, A] | p[*, B] | p[*, C] | p[*, D] | p[*, E] | |
|---|---|---|---|---|---|
| p[A, *] | 28 | 28 | 30 | 24 | |
| p[B, *] | 25 | 28 | 33 | 24 | |
| p[C, *] | 25 | 29 | 29 | 24 | |
| p[D, *] | 25 | 28 | 28 | 24 | |
| p[E, *] | 25 | 28 | 28 | 31 |
По методу Шульце будет провозглашён победителем кандидат E, так как p[E, X] ⩾ p[X, E] для любого другого кандидата X.
Так как 25 = p[E, A] > p[A, E] = 24, кандидат E лучше, чем кандидат A.
Так как 28 = p[E, B] > p[B, E] = 24, кандидат E лучше, чем кандидат B.
Так как 28 = p[E, C] > p[C, E] = 24, кандидат E лучше, чем кандидат C.
Так как 31 = p[E, D] > p[D, E] = 24, кандидат E лучше, чем кандидат D.
Так как 28 = p[A, B] > p[B, A] = 25, кандидат A лучше, чем кандидат B.
Так как 28 = p[A, C] > p[C, A] = 25, кандидат A лучше, чем кандидат C.
Так как 30 = p[A, D] > p[D, A] = 25, кандидат A лучше, чем кандидат D.
Так как 29 = p[C, B] > p[B, C] = 28, кандидат C лучше, чем кандидат B.
Так как 29 = p[C, D] > p[D, C] = 28, кандидат C лучше, чем кандидат D.
Так как 33 = p[B, D] > p[D, B] = 28, кандидат B лучше, чем кандидат D.
Таким образом, метод Шульце приводит к следующему порядку кандидатов: E > A > C > B > D.
Применение
Метод Шульце пока не применяется на общеполитических выборах, но он становится всё более популярным в частных организациях. На сегодняшний день он применяется на выборах в следующих частных организациях и партиях:
- Annodex Association[1]
- Blitzed[2]
- BoardGameGeek[3]
- Cassandra[4]
- Codex Alpe Adria[5]
- Collective Agency[6]
- College of Marine Science[7]
- Computer Science Departmental Society for York University (HackSoc)[8]
- County Highpointers[9]
- Debian[10]
- Demokratische Bildung Berlin[11]
- EuroBillTracker[12]
- European Democratic Education Conference (EUDEC)[13]
- Fair Trade Northwest[14]
- FFmpeg[15]
- Flemish Student Society of Leuven[16]
- Free Geek[17]
- Free Hardware Foundation of Italy[18]
- Free Software Foundation Europe (FSFE)[19]
- Gentoo Foundation[20]
- GNU Privacy Guard (GnuPG)[21]
- Gothenburg Hacker Space (GHS)[22]
- Graduate Student Organization at the State University of New York: Computer Science (GSOCS)[23]
- Haskell[24]
- Ithaca Generator[25]
- Kanawha Valley Scrabble Club[26]
- KDE e.V.[27]
- Kingman Hall[28]
- Knight Foundation[29]
- Kumoricon[30]
- League of Professional System Administrators (LOPSA)[31]
- Libre-Entreprise[32]
- LiquidFeedback[33]
- Lumiera/Cinelerra[34]
- Mathematical Knowledge Management Interest Group (MKM-IG)[35]
- Metalab[36]
- Music Television (MTV)[37]
- Neo[38]
- Noisebridge[39]
- North Shore Cyclists (NSC)[40]
- OpenEmbedded[41]
- OpenStack[42]
- Park Alumni Society (PAS)[43]
- Пиратская партия Австралии[44]
- Пиратская партия Австрии[45]
- Пиратская партия Бельгии[46]
- Пиратская партия Бразилии
- Пиратская партия Франции[47]
- Пиратская партия Германии[48]
- Пиратская партия Италии[49]
- Пиратская партия Мексики[50]
- Пиратская партия Новой Зеландии[51]
- Пиратская партия Швеции[52]
- Пиратская партия Швейцарии[53]
- Пиратская партия США[54]
- Pitcher Plant of the Month
- Pittsburgh Ultimate[55]
- RLLMUK[56]
- RPMrepo[57]
- Sender Policy Framework (SPF)[58]
- Software in the Public Interest (SPI)[59]
- Squeak[60]
- Students for Free Culture[61]]
- Sugar Labs[62]
- Sverok[63]
- TestPAC[64]
- TopCoder[65]
- Ubuntu[66]
- University of British Columbia Math Club[67]
- Фонд Викимедиа[68]
- Википедия на французском,[69] иврите,[70] венгерском[71] и русском[72].
Альтернативное голосование
Метод Шульце представляет собой развитие идеи альтернативного голосования, которое применяется при выборах в различные органы власти Австралии, Новой Зеландии, Папуа — Новой Гвинеи, Фиджи, Ирландии, США, а также в ряде политических партий, неправительственных организаций и т. д.
Примечания
- Election of the Annodex Association committee for 2007, February 2007.
- Condorcet method for admin voting. Архивная копия от 26 апреля 2005 на Wayback Machine, January 2005.
-
- Important notice for Golden Geek voters, September 2007.
- Golden Geek Awards 2008 — Nominations Open, August 2008.
- Golden Geek Awards 2009 — Nominations Open, August 2009.
- Golden Geek Awards 2010 — Nominations Open, September 2010.
- Golden Geek Awards 2011 — Nominations Open, September 2011.
- Project Logo Архивная копия от 3 октября 2015 на Wayback Machine, October 2009.
- Codex Alpe Adria Competitions. 0xaa.org (24 января 2010). Дата обращения: 8 мая 2010. Архивировано 2 февраля 2013 года.
- Civics Meeting Minutes (недоступная ссылка), March 2012.
- Fellowship Guidelines (PDF) (недоступная ссылка). Дата обращения: 1 июня 2011. Архивировано 28 сентября 2011 года.
- Report on HackSoc Elections, December 2008.
- Adam Helman, Family Affair Voting Scheme — Schulze Method.
-
- Appendix 1 of the constitution. Архивная копия от 18 июля 2011 на Wayback Machine
-
- Candidate cities for EBTM05, December 2004.
- Meeting location preferences, December 2004.
- Date for EBTM07 Berlin, January 2007.
- Vote the date of the Summer EBTM08 in Ljubljana, January 2008.
- New Logo for EBT, August 2009.
- Guidance Document. Eudec.org (15 ноября 2009). Дата обращения: 8 мая 2010. Архивировано 2 февраля 2013 года.
- Article XI, section 2 of the bylaws Архивная копия от 26 июля 2011 на Wayback Machine
- Democratic election of the server admins. Архивная копия от 2 октября 2015 на Wayback Machine, July 2010.
- Article 51 of the statutory rules.
- Voters Guide, September 2011.
-
- Eletto il nuovo Consiglio nella Free Hardware Foundation Архивная копия от 25 декабря 2008 на Wayback Machine, June 2008.
- Poll Results, June 2008.
-
- article 6 section 3 of the constitution.
- Fellowship vote for General Assembly seats, March 2009.
- And the winner of the election for FSFE’s Fellowship GA seat is …, June 2009.
-
- Gentoo Foundation Charter Архивировано 22 августа 2011 года.
- Aron Griffis, 2005 Gentoo Trustees Election Results Архивная копия от 3 октября 2015 на Wayback Machine, May 2005.
- Lars Weiler, Gentoo Weekly Newsletter 23 May 2005. Архивная копия от 2 октября 2015 на Wayback Machine
- Daniel Drake, Gentoo metastructure reform poll is open. Архивная копия от 3 октября 2015 на Wayback Machine, June 2005.
- Grant Goodyear, Results now more official. Архивная копия от 25 сентября 2015 на Wayback Machine, September 2006.
- 2007 Gentoo Council Election Results. Архивная копия от 23 декабря 2010 на Wayback Machine, September 2007.
- 2008 Gentoo Council Election Results. Архивная копия от 23 декабря 2010 на Wayback Machine, June 2008.
- 2008 Gentoo Council Election Results. Архивная копия от 23 декабря 2010 на Wayback Machine, November 2008.
- 2009 Gentoo Council Election Results. Архивная копия от 7 июня 2011 на Wayback Machine, June 2009.
- 2009 Gentoo Council Election Results. Архивная копия от 23 декабря 2010 на Wayback Machine, December 2009.
- 2010 Gentoo Council Election Results. Архивная копия от 23 декабря 2010 на Wayback Machine, June 2010.
- GnuPG Logo Vote. Архивная копия от 16 декабря 2006 на Wayback Machine, November 2006.
- § 14 of the bylaws. Архивная копия от 29 апреля 2010 на Wayback Machine
- User Voting Instructions (недоступная ссылка). Gso.cs.binghamton.edu. Дата обращения: 8 мая 2010. Архивировано 2 февраля 2013 года.
- Haskell Logo Competition, March 2009.
- Article VI, section 10 of the bylaws (недоступная ссылка), November 2012.
- A club by any other name …, April 2009.
- section 3.4.1 of the Rules of Procedures for Online Voting.
-
- Ka-Ping Yee, Condorcet elections, March 2005.
- Ka-Ping Yee, Kingman adopts Condorcet voting, April 2005.
- Knight Foundation awards $5000 to best created-on-the-spot projects Архивная копия от 20 июля 2011 на Wayback Machine, June 2009.
-
- Mascot 2007 contest, July 2006.
- Mascot 2008 and cover 2007 contests, May 2007.
- Mascot 2009 and program cover 2008 contests, April 2008.
- Mascot 2010 and program cover 2009 contests, May 2009.
- Mascot 2011 and book cover 2010 contests, May 2010.
- Mascot 2012 and book cover 2011 contests, May 2011.
- Article 8.3 of the bylaws.
- Concepts. Home page of LiquidFeedback. Interactive Democracy. Дата обращения: 26 декабря 2012. Архивировано 2 февраля 2013 года.
- Lumiera Logo Contest, January 2009.
- The MKM-IG uses Condorcet with dual dropping:
- MKM-IG Charter.
- Michael Kohlhase, MKM-IG Trustees Election Details & Ballot. Архивировано 9 декабря 2012 года., November 2004.
- Andrew A. Adams, MKM-IG Trustees Election 2005. Архивировано 9 декабря 2012 года., December 2005.
- Lionel Elie Mamane, Elections 2007: Ballot. Архивировано 9 декабря 2012 года., August 2007.
- Wahlmodus (нем.). Metalab.at. Дата обращения: 8 мая 2010.
- Benjamin Mako Hill, Voting Machinery for the Masses, July 2008.
-
- Wahlen zum Neo-2-Freeze: Formalitäten Архивная копия от 27 июля 2011 на Wayback Machine, February 2010.
- Hinweise zur Stimmabgabe, March 2010.
- Ergebnisse, March 2010.
- 2009 Director Elections.
- NSC Jersey election Архивная копия от 26 марта 2009 на Wayback Machine, NSC Jersey vote, September 2007.
- Online Voting Policy.
-
- 2010 OpenStack Community Election, November 2010.
- OpenStack Governance Elections Spring 2012, February 2012.
- Voting Procedures (недоступная ссылка). Parkscholars.org. Дата обращения: 8 мая 2010. Архивировано 13 апреля 2013 года.
- National Congress 2011 Results, November 2011.
- § 6(10) of the bylaws. Архивная копия от 11 мая 2012 на Wayback Machine
- Ik word Piraat! (недоступная ссылка), August 2012.
- § 11.2.E of the statutory rules. Архивная копия от 23 марта 2013 на Wayback Machine
- 11 из 16 региональных организаций и федеральная организация Пиратской партии Германии используют LiquidFeedback для внутрипартийных голосований. В 2010—2011 годах Пиратские партии Neukölln (link), Mitte (link), Steglitz-Zehlendorf (link), Lichtenberg (link), и Tempelhof-Schöneberg (link) приняли метод Шульце для внутрипартийных выборов. Также Пиратская партия Берлина (в 2011 году) (link) и Пиратская партия Регенсбурга (в 2012 году) (link) одобрила этот метод для внутрипартийных выборов.
- Rules adopted on 18 December 2011 (недоступная ссылка).
- Vote Result for Name Definition (недоступная ссылка).
- 23 January 2011 meeting minutes.
-
- Inför primärvalen, October 2009.
- Dags att kandidera till riksdagen, October 2009.
- Råresultat primärvalet, January 2010.
- Piratenversammlung der Piratenpartei Schweiz, September 2010.
- Article IV, section 4 of the constitution. Архивная копия от 9 ноября 2012 на Wayback Machine
- 2006 Community for Pittsburgh Ultimate Board Election, September 2006.
- Committee Elections, April 2012.
- LogoVoting Архивная копия от 13 июня 2010 на Wayback Machine, December 2007.
-
- SPF Council Election Procedures. Архивная копия от 16 июля 2011 на Wayback Machine
- 2006 SPF Council Election, January 2006.
- 2007 SPF Council Election, January 2007.
- Process for adding new board members, January 2003.
- Squeak Oversight Board Election 2010, March 2010.
-
- Bylaws of the Students for Free Culture, article V, section 1.1.1.
- [http://blog.selectricity.org/?p=4 Free Culture Student Board Elected Using Selectricity. Архивная копия от 15 декабря 2010 на Wayback Machine, February 2008.
- Election status update, September 2009.
- Minutes of the 2010 Annual Sverok Meeting, November 2010.
- Article VI, section 6 of the bylaws. Архивная копия от 30 января 2012 на Wayback Machine
-
- 2006 TopCoder Open Logo Design Contest, November 2005.
- 2006 TopCoder Collegiate Challenge Logo Design Contest, June 2006.
- 2007 TopCoder High School Tournament Logo. Архивная копия от 17 июля 2011 на Wayback Machine, September 2006.
- 2007 TopCoder Arena Skin Contest. Архивная копия от 17 июля 2011 на Wayback Machine, November 2006.
- 2007 TopCoder Open Logo Contest. Архивная копия от 17 июля 2011 на Wayback Machine, January 2007.
- 2007 TopCoder Open Web Design Contest. Архивная копия от 17 июля 2011 на Wayback Machine, January 2007.
- 2007 TopCoder Collegiate Challenge T-Shirt Design Contest. Архивная копия от 17 июля 2011 на Wayback Machine, September 2007.
- 2008 TopCoder Open Logo Design Contest. Архивная копия от 17 июля 2011 на Wayback Machine, September 2007.
- 2008 TopCoder Open Web Site Design Contest. Архивная копия от 17 июля 2011 на Wayback Machine, October 2007.
- 2008 TopCoder Open T-Shirt Design Contest. Архивная копия от 17 июля 2011 на Wayback Machine, March 2008.
- Ubuntu IRC Council Position, May 2012.
- this mail.
-
- Jesse Plamondon-Willard, Board election to use preference voting, May 2008.
- Mark Ryan, 2008 Wikimedia Board Election results, June 2008.
- 2008 Board Elections, June 2008.
- 2009 Board Elections, August 2009.
- Choix dans les votes.
- here (May 2009), here (August 2009), and here (December 2009).
- here and here.
-
- Result of 2007 Arbitration Committee Elections.Архивированная копия (недоступная ссылка). Дата обращения: 17 января 2022. Архивировано 11 мая 2009 года.
- Result of 2008 Arbitration Committee Elections.Архивированная копия (недоступная ссылка). Дата обращения: 17 января 2022. Архивировано 28 мая 2009 года.
- Result of 2009 Arbitration Committee Elections.Архивированная копия (недоступная ссылка). Дата обращения: 25 февраля 2022. Архивировано 27 ноября 2009 года.
- Result of 2010 Arbitration Committee Elections.Архивировано 16 апреля 2011 года.
