Gerasim@Home
Gerasim@Home — российский проект добровольных распределенных вычислений на платформе BOINC. Проект стартовал в тестовом режиме в феврале 2008 года[1]. Отличительной особенностью серверной части проекта, разработанной С. Ю. Валяевым, является использование операционной системы Windows Server 2008 и связки Microsoft SQL Server с ASP.NET, в то время как стандартный набор приложений от разработчиков BOINC требует использования операционной системы Linux или Unix. По состоянию на 23 июля 2015 года в проекте приняли участие 1999 пользователей (890 компьютеров) из 62 стран, обеспечивая производительность 1—5 терафлопс. Участвовать в проекте может любой желающий, обладающий компьютером с выходом в Интернет, установив на него программу BOINC Manager.
| Gerasim@Home | |
|---|---|
| Платформа | BOINC |
| Объём загружаемого ПО | 2 МБ |
| Объём загружаемых данных задания | 1 КБ |
| Объём отправляемых данных задания | 150 КБ |
| Объём места на диске | 2 МБ |
| Используемый объём памяти | 10 МБ |
| Графический интерфейс | нет |
| Среднее время расчёта задания | до 6 часов |
| Deadline | 11 дней |
| Возможность использования GPU | нет |
История проекта
Проект стартовал в тестовом режиме в феврале 2008 года[1], используя в качестве тестового расчетного модуля программу gsm для поиска простых чисел.
В июне 2010 года на кафедре вычислительной техники Юго-Западного государственного университета было разработано расчетное приложение separator, целью которого является построение разбиений параллельных граф-схем алгоритмов логического управления, получаемых различными эвристическими методами, с целью сравнения качества получаемых решений и выработки рекомендаций о границах целесообразности применения методов. Первая часть расчетов была завершена в сентябре 2011 г.
В январе 2013 года был начат эксперимент[2] по исследованию возможностей применения жадной стратегии синтеза разбиения с ограничением на выбор вершин из смежной окрестности текущего блока[3].
В марте 2014 года начата новая серия экспериментов, целью которой является апробация применения эвристических методов применительно к решению известных задач теории графов на примере задачи поиска кратчайшего пути в графе и для поиска разбиений[4].
В июне 2014 года стартовала серия экспериментов с целью исследования возможности использования случайного перебора[5][6] с фиксированным числом итераций при построении разбиений.
В феврале 2015 года запущено продолжение серии экспериментов, целью которых является апробация применения эвристических методов применительно к решению задачи поиска кратчайшего пути в графе с использованием возвратной стратегии[7], а также методов имитации отжига[8], перебора с ограничением глубины[9][10], различных вариаций муравьиного алгоритма[11][12], генетического алгоритма[13] и алгоритма пчелиной колонии[14].
В июне 2016 года запущен вычислительный эксперимент, целью которого является подсчет числа диагональных латинских квадратов порядка 9 (последовательность A274171 в OEIS и последовательность A274806 в OEIS)[15].
В октябре 2016 в проекте был начат эксперимент, направленный на исследование эффективности методов случайных блужданий[16] и роя частиц[17][18] в задаче поиска кратчайшего пути в графе.

В начале 2017 года в проекте был организован эксперимент, направленный на определение значений ряда комбинаторных характеристик диагональных латинских квадратов и их ортогональных пар (греко-латинских квадратов) порядка 8[19]. В марте 2017 стартовал эксперимент по получению случайных пар ортогональных диагональных латинских квадратов порядка 10 с целью формирования списка их уникальных канонических форм[20]. С 3 по 16 июня 2017 года в проекта осуществлялся подсчет числа симметричных диагональных латинских квадратов порядка 10[21]. 23 октября 2017 года в проекта запущен эксперимент, направленный на анализ симметричных в одной плоскости квадратов при построении пар ортогональных диагональных латинских квадратов[22][23].
В декабре 2018 года в проекте был начат эксперимент по изучению эффективности эвристических методов в задаче раскраски графов общего вида[24].
Приложение separator
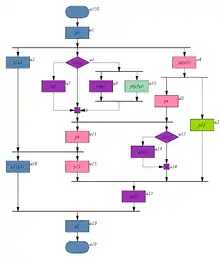
Необходимость в отыскании разбиения, (суб)оптимального по ряду показателей качества, возникает при проектировании систем логического управления, используемых для осуществления логического управления различными дискретными системами (цифровыми схемами, станками с ЧПУ, роботизированными сборочными линиями и т. д.). При проектировании подобных систем возникает ряд комбинаторных многокритериальных оптимизационных задач на дискретных структурах (графах), к которым и относится задача синтеза разбиения заданной граф-схемы алгоритма управления[25][26][27], в соответствии с которым должна работать разрабатываемая система логического управления. Отыскание точного решения (глобального оптимума) в большинстве практических случаев невозможно из-за того, что поставленная задача принадлежит к классу NP, поэтому на практике обычно ограничиваются применением эвристических методов, дающих решения неплохого качества за приемлемое время.
Качество найденного решения оценивается как степень минимизации частных показателей качества, к которым относятся:
- число блоков разбиения — совпадает с числом контроллеров в составе системы логического управления, напрямую влияет на аппаратную сложность системы системы логического управления, её энергопотребление и массогабаритные характеристики;
- степени дублирования сигналов логических условий и микроопераций — определяют оптимальность распределения вершин граф-схемы алгоритма по блокам разбиения, влияют на число дорожек, связывающих контроллеры на печатной плате или в составе интегральной микросхемы (в зависимости от выбранного способа реализации системы логического управления);
- сложность сети межблочных связей — определяет необходимое число микрокоманд передачи управления между контроллерами, влияет на глубины некоторых очередей в составе коммуникационной подсистемы контроллера;
- интенсивность межблочных взаимодействий — определяет среднее число передач управления за время выполнения заданного управляющего алгоритма (межконтроллерный трафик передачи управления), влияет на быстродействие системы управления в целом.
Интегральная оценка качества разбиения рассчитывается как взвешенная сумма нормированных значений частных показателей качества.
При практической реализации системы логического управления приходится учитывать ограничения технологического характера, к которым в первую очередь относятся:
- число ножек на корпусе микросхемы для приема сигналов логических условий и выдачи сигналов микроопераций ;
- объём памяти микрокоманд в составе контроллера.
Ограничение не является критическим и может быть исключено из рассмотрения путём дублирования контроллеров, имеющих одинаковые входы и выпоняющих однотипные микропрограммы. С целью упрощения внутренней структуры контроллера накладывается дополнительное структурное ограничение на невозможность размещения параллельных вершин в составе одного блока разбиения (контроллера).
В качестве эвристических методов поиска разбиений в вычислительных экспериментах принимали участие:
- метод С. И. Баранова[28] и его модификации[3] — используют жадную стратегию последовательного формирования блоков разбиения;
- метод параллельно-последовательной декомпозиции[29][30] — использует ряд эквивалентных преобразований (разрыв циклов, объединение линейных участков граф-схемы алгоритма, классификация отношений между вершинами граф-схемы, построение множества сечений граф-схемы, построение блоков разбиения на основании анализа таблиц включений);
- метод случайного перебора[5][6] с заданным числом итераций.
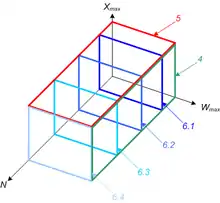
Методы характеризуются существенно различной трудоемкостью реализации, временной и емкостной сложностью алгоритмов преобразований и качеством получаемых решений при различных значениях технологических ограничений. При проведении сравнения качества методов необходимо исследование различных областей пространства параметров , где — число вершин в составе граф-схем алгоритмов, что является вычислительно сложной задачей. В процессе расчетов были проанализированы отдельные срезы пространства параметров, на основании чего было выявлено существенно различное поведение методов синтеза разбиений по мере усиления или ослабления значений технологических ограничений.



Для каждой точки выбранного среза пространства параметров осуществляется построение выборки параллельных алгоритмов логического управления с псевдослучайной структурой, построение их разбиений указанным методом и оценка качества, что требует от нескольких минут (малые значения ) до нескольких часов (большие значения ) вычислительного времени. Полученные выборки числовых значений объёмом около 200 КБ каждая передаются на сервер проекта и ожидают последующей обработки. Общий объём полученных данных (без учета избыточности) составил 235 ГБ, а вычислительные затраты — 51,6 экзафлоп (818 ГГц-лет). По сравнению с реализацией на двухъядерном процессоре Core 2 Duo с частотой 1,86 ГГц выигрыш во времени, полученный за счет параллельной обработки с использованием грид, составил 155 раз. Постобработка полученных результатов[31][32] заняла около суток вычислительного времени и заключалась в расчете средних значений параметров качества и вероятностей получения разбиения с минимальным значением выбранного показателя качества, в результате чего были получены искомые двумерные карты общим объёмом 96 МБ, которые можно использовать для подробного анализа поведения методов в различных областях пространства параметров.
Приложение spstarter
В марте 2014 года стартовала[4] очередная серия вычислительных экспериментов, отличительной особенностью которой является поддержка одновременного выполнения нескольких экспериментов. С целью тестирования методов решения дискретных оптимизационных задач был реализован соответствующий расчетный модуль, статически подключаемый к приложению spstarter.exe. Помимо приложения separator, вошедшего в состав нового расчетного модуля, реализована возможность анализа качества решений тестовой задачи нахождения кратчайшего пути в графе с использованием ряда подходов (алгоритм Дейкстры, жадный алгоритм, случайный перебор, взвешенный случайный перебор[33], их модификации с поддержкой комбинаторных возвратов[7], вариации алгоритма муравьиной колонии[11][12], метод имитации отжига, перебор с ограничением глубины или числа рассматриваемых ветвей дерева, генетический алгоритм[13], алгоритм пчелиной колонии[14], метод случайных блужданий и вариации метода роя частиц) с целью выявления их сильных и слабых сторон. Наилучшие результаты были в рассматриваемой задаче были продемонстрированы методом муравьиной колонии и генетическим алгоритмом[34][35], [36].
Определение асимптотического поведения комбинаторных характеристик комбинаторных структур на базе диагональных латинских квадратов
Асимптотическое поведение числа диагональных латинских квадратов (ДЛК) с ростом их размерности N до выполненных в проекте расчетов было неизвестно. В результате разработки высокоэффективного расчетного модуля, который использует ряд приемов алгоритмической и высокоуровневой оптимизации[37][38][39][40][41][42], удалось достичь темпа генерации в 6,6 млн. ДЛК/с, что позволило определить число ДЛК до N<10 (последовательность A274171 в OEIS и последовательность A274806 в OEIS). Для этого потребовалось 3 месяца расчетов на грид с реальной производительностью 2—5 TFLOP/s[43] и 3 месяца расчетов на вычислительном кластере «Академик В.М. Матросов» СО РАН с целью проверки и подтверждения полученного результата[44].
С использованием аналогичных алгоритмических принципов был осуществлен подсчет числа симметричных диагональных латинских квадратов порядка N<11[21] и определение минимального и максимального числа трансверсалей в диагональных латинских квадратах порядка N<9[45][46][47].
Кроме определения комбинаторных характеристик, в проекте производится поиск и коллекционирование канонических форм ортогональных диагональных латинских квадратов порядка 10 с целью классификации образуемых ими комбинаторных структур (графов на множестве бинарного отношения ортогональности)[48] и попыткой отыскания тройки попарно-ортогональных диагональных латинских квадратов, что является открытой математической проблемой. Наиболее эффективно поиск ортогональных квадратов общего вида осуществляется с использованием трансверсалей путем сведения исходной задачи к задаче о точном покрытии с последующем ее решением с использованием алгоритма танцующих связей в рамках метода Эйлера-Паркера[49][50]. По состоянию на июль 2020 г. коллекция включает более 10 млн. канонических форм ОДЛК порядка 10, найденных в проекте.
Научные достижения
- получены границы областей применимости методов синтеза разбиений: область слабых ограничений для метода С. И. Баранова, область сильных ограничений для метода параллельно-последовательной декомпозиции (качественное преимущество);
- получены отношения степени оптимизации каждого из выбранных показателей качества к известному для него условному оптимуму, для каждого из методов показан проигрыш в процентах (количественное превосходство);
- получены границы областей нечувствительности, в которых ослабление ограничений не влияет на повышение качества решений, область нечувствительности имеет различную ширину для различных эвристических методов;
- сформулированы рекомендации для разработчиков аппаратной части мультиконтроллеров, структура логического мультиконтроллера с большим числом простых контроллеров является предпочтительной; показана диктуемая практикой необходимость работы в области сильных ограничений;
- произведен подсчет числа диагональных латинских квадратов порядка N<10 (последовательность A274171 в OEIS и последовательность A274806 в OEIS);
- произведен подсчет числа горизонтально симметричных диагональных латинских квадратов порядка N<11 (последовательность A287649 в OEIS и последовательность A292516 в OEIS);
- произведен подсчет числа дважды симметричных диагональных латинских квадратов порядка N<10 (последовательность A287650 в OEIS и последовательность A292517 в OEIS);
- произведен подсчет числа симметричных в одной плоскости диагональных латинских квадратов порядка N<9 (последовательность A296060 в OEIS и последовательность A296061 в OEIS);
- произведен подсчет числа редуцированных (первая строка квадратов упорядочена, например, по возрастанию) пар ортогональных диагональных латинских квадратов порядка N<8 (последовательность A287651 в OEIS);
- произведен подсчет максимально возможного числа диагональных латинских квадратов, ортогональных одному диагональному латинскому квадрату порядка N<9 (последовательность A287695 в OEIS);
- произведен подсчет числа и анализ свойств главных классов диагональных латинских квадратов порядка N<9 (последовательность A287764 в OEIS, последовательность A299783 в OEIS, последовательность A299784 в OEIS, последовательность A299785 в OEIS и последовательность A299787 в OEIS)[51][52];
- произведен подсчет числа центрально симметричных диагональных латинских квадратов порядка N<10 (последовательность A293777 в OEIS и последовательность A293778 в OEIS)[53][54];
- произведено определение минимального и максимального числа трансверсалей в диагональных латинских квадратах порядка N<9 (последовательность A287644 в OEIS, последовательность A287645 в OEIS, последовательность A287647 в OEIS и последовательность A287648 в OEIS);
- произведен подсчет числа пандиагональных латинских квадратов порядка N с фиксированной первой строкой (последовательность A123565 в OEIS);
- произведен подсчет числа ортогональных (ODLS), самоортогональных (SODLS), дважды самоортогональных (DSODLS) и расширенных самоортогональных (ESODLS) диагональных латинских квадратов порядка 1—10, а также нормализованных квадратов для того же типа ортогональности и их главных классов (последовательность A330391 в OEIS}, последовательность A329685 в OEIS, последовательность A333366 в OEIS, последовательность A309210 в OEIS)[55];
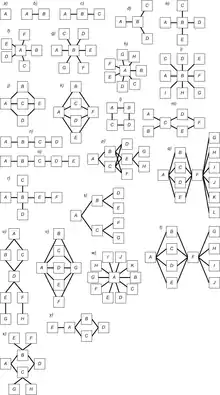
- произведена классификация комбинаторных структур, возникающих из диагональных латинских квадратов порядка 1—10 на множестве бинарного отношения ортогональности[56][57][48];
- показано, что рекордная характеристика ортогональности 274[58] для псевдотройки попарно-ортогональных диагональных латинских квадратов порядка 10, найденная в ходе анализа плоскостной симметрии в ДЛК, не может быть улучшена как в данном классе симметрий, так и в классе чистых обобщенных симметрий и их окрестностей.

Примечания
- BOINCstats | Gerasim@Home — Credit overview (недоступная ссылка)
- Separator progress - Page 2 - Science - Forum Gerasim@home (недоступная ссылка). Дата обращения: 30 января 2013. Архивировано 4 февраля 2013 года.
- Ватутин Э. И., Леонов М. Е. Использование смежной окрестности при жадном последовательном формировании блоков разбиения граф-схем параллельных алгоритмов // Известия высших учебных заведений. Приборостроение. 2013. Т. 56. № 6. С. 30-35.
- О проекте Gerasim@home — Page 48 — Gerasim@home — Форум Boinc.ru (недоступная ссылка)
- Ватутин Э. И., Колясников Д. В., Мартынов И. А., Титов В. С. Метод случайного перебора в задаче построения разбиений граф-схем параллельных алгоритмов // Многоядерные процессоры, параллельное программирование, ПЛИС, системы обработки сигналов. Барнаул: Барнаул, 2014. С. 115—125.
- Ватутин Э. И., Колясников Д. В., Титов В. С. Анализ результатов применения метода случайного перебора в задаче поиска разбиений граф-схем параллельных алгоритмов // Известия Южного федерального университета. Технические науки. 2014. № 12 (161). С. 102—110.
- Ватутин Э. И., Мартынов И. А., Титов В. С. Способ обхода тупиков при решении задач дискретной оптимизации с ограничениями // Перспективные информационные технологии (ПИТ-2014). Самара: изд-во Самарского научного центра РАН. С. 313—317.
- Ватутин Э. И., Титов В. С. Параметрическая оптимизация алгоритма имитации отжига на примере решения задачи поиска кратчайшего пути в графе // Вестник Череповецкого государственного университета. № 6 (67). 2015. С. 13-16.
- О проекте Gerasim@home — Page 63 — Gerasim@home — Форум Boinc.ru (недоступная ссылка). Дата обращения: 16 февраля 2015. Архивировано 16 февраля 2015 года.
- Ватутин Э. И., Мартынов И. А., Титов В. С. Анализ результатов использования метода перебора с ограничением глубины в задаче поиска кратчайшего пути в графе // Многоядерные процессоры, параллельное программирование, ПЛИС, системы обработки сигналов (МППОС’15). Барнаул, 2015. С. 120—128.
- Ватутин Э. И., Титов В. С. Анализ результатов применения алгоритма муравьиной колонии в задаче поиска пути в графе при наличии ограничений // Известия Южного федерального университета. Технические науки. 2014. № 12 (161). С. 111—120.
- Ватутин Э. И., Титов В. С. Об одном подходе к использованию алгоритма муравьиной колонии при решении задач дискретной комбинаторной оптимизации // Интеллектуальные и информационные системы (Интеллект 2015). Тула, 2015. С. 8-13.
- Ватутин Э. И., Титов В. С. Исследование особенностей применения генетического алгоритма в задаче поиска кратчайшего пути в графе при наличии ограничений на плотность графа // Многоядерные процессоры, параллельное программирование, ПЛИС, системы обработки сигналов (МППОС — 2016). Барнаул: изд-во Алтайского государственного университета, 2016. С. 152—159.
- Ватутин Э. И., Титов В. С. Особенности метаоптимизации алгоритма пчелиной колонии в задаче поиска кратчайшего пути в графе при наличии ограничений на плотность графа // Известия Юго-Западного государственного университета. Серия: Управление, вычислительная техника, информатика. Медицинское приборостроение. № 2 (19). 2016. С. 52-65.
- Project News
- О проекте Gerasim@home — Page 94 — Gerasim@home — Форум Boinc.ru (недоступная ссылка). Дата обращения: 22 ноября 2016. Архивировано 22 ноября 2016 года.
- О проекте Gerasim@home — Page 96 — Gerasim@home — Форум Boinc.ru (недоступная ссылка). Дата обращения: 22 ноября 2016. Архивировано 22 ноября 2016 года.
- Ватутин Э.И., Титов В.С. Исследование особенностей применения метода роя частиц в задачах дискретной оптимизации // Вестник компьютерных и информационных технологий. № 5 (167). 2018. С. 26–34. DOI: 0.14489/vkit.2018.05.pp.026–034.
- О проекте Gerasim@home - Page 98 - Gerasim@home - Форум Boinc.ru (недоступная ссылка). Дата обращения: 14 марта 2017. Архивировано 15 марта 2017 года.
- Поиск КФ ОДЛК в проекте Gerasim@home - Gerasim@home - Форум Boinc.ru (недоступная ссылка). Дата обращения: 14 марта 2017. Архивировано 15 марта 2017 года.
- О проекте Gerasim@home - Page 103 - Gerasim@home - Форум Boinc.ru (недоступная ссылка). Дата обращения: 16 июня 2017. Архивировано 20 июня 2017 года.
- О проекте Gerasim@home - Page 106 - Gerasim@home - Форум Boinc.ru (недоступная ссылка). Дата обращения: 29 октября 2017. Архивировано 30 октября 2017 года.
- Ватутин Э.И., Кочемазов С.Е., Заикин О.С., Титов В.С. Исследование свойств симметричных диагональных латинских квадратов. Работа над ошибками // Интеллектуальные и информационные системы (Интеллект – 2017). Тула, 2017. С. 30–36.
- О проекте Gerasim@home - Page 117 - Gerasim@home - Форум Boinc.ru (недоступная ссылка). Дата обращения: 20 декабря 2018. Архивировано 20 декабря 2018 года.
- Зотов И. В., Титов В. С., Колосков В. А. [и др.] Организация и синтез микропрограммных мультимикроконтроллеров. Курск: изд-во «Курск», 1999. 368 с. ISBN 5-7277-0253-4
- Ватутин Э. И., Зотов И. В., Титов В. С. [и др.] Комбинаторно-логические задачи синтеза разбиений параллельных алгоритмов логического управления при проектировании логических мультиконтроллеров. Курск, изд-во КурскГТУ, 2010. 200 с. ISBN 978-5-7681-0523-5
- Ватутин Э. И. Проектирование логических мультиконтроллеров. Синтез разбиений параллельных граф-схем алгоритмов. Saarbrucken: Lambert Academic Publishing, 2011 г. 292 с. ISBN 978-3-8433-1728-3
- Баранов С. И., Журавина Л. Н., Песчанский В. А. Метод представления параллельных граф-схем алгоритмов совокупностями последовательных граф-схем // Автоматика и вычислительная техника. 1984. № 5. С. 74—81.
- Зотов И. В., Колосков В. А., Титов В. С. Выбор оптимальных разбиений алгоритмов при проектировании микроконтроллерных сетей // Автоматика и вычислительная техника. 1997. № 5. С. 51—62.
- Ватутин Э. И., Зотов И. В. Метод формирования субоптимальных разбиений параллельных управляющих алгоритмов // Параллельные вычисления и задачи управления (PACO’04). М.: ИПУ РАН, 2004. С. 884—917.
- evatutin — Расчеты и постобработка завершены!
- evatutin — Постобработка результатов анализа смежной жадной стратегии завершена!
- Ватутин Э. И., Дремов Е. Н., Мартынов И. А., Титов В. С. Метод взвешенного случайного перебора для решения задач дискретной комбинаторной оптимизации // Известия ВолГТУ. Серия: Электроника, измерительная техника, радиотехника и связь. № 10 (137). Вып. 9. 2014. c. 59-64.
- Vatutin E.I. Comparison of Decisions Quality of Heuristic Methods with Sequential Formation of the Decision in the Graph Shortest Path Problem // CEUR Workshop Proceedings. Proceedings of the Third International Conference BOINC-based High Performance Computing: Fundamental Research and Development (BOINC:FAST 2017). Vol. 1973. Technical University of Aachen, Germany, 2017. pp. 67–76.
- Vatutin E.I. Comparison of Decisions Quality of Heuristic Methods with Limited Depth-First Search Techniques in the Graph Shortest Path Problem // Open Engineering. Vol. 7. Iss. 1. 2017. pp. 428–434. DOI: 10.1515/eng-2017-0041.
- Vatutin E., Panishchev V., Gvozdeva S., Titov V. Comparison of Decisions Quality of Heuristic Methods Based on Modifying Operations in the Graph Shortest Path Problem // Problems of Information Technology. No. 1. 2020. pp. 3–15. DOI: 10.25045/jpit.v11.i1.01.
- Ватутин Э. И., Журавлев А. Д., Заикин О. С., Титов В. С. Особенности использования взвешивающих эвристик в задаче поиска диагональных латинских квадратов // Известия Юго-Западного государственного университета. Серия: Управление, вычислительная техника, информатика. Медицинское приборостроение. 2015. № 3 (16). С. 18-30.
- Vatutin E.I., Zaikin O.S., Zhuravlev A.D., Manzuk M.O., Kochemazov S.E., Titov V.S. Using grid systems for enumerating combinatorial objects on example of diagonal Latin squares // Distributed computing and grid-technologies in science and education (GRID’16): book of abstracts of the 7th international conference. Dubna: JINR, 2016. p. 114—115.
- Ватутин Э. И., Заикин О. С., Журавлев А. Д., Манзюк М. О., Кочемазов С. Е., Титов В. С. О влиянии порядка заполнения ячеек на темп генерации диагональных латинских квадратов // Информационно-измерительные диагностирующие и управляющие системы (Диагностика — 2016). Курск: изд-во ЮЗГУ, 2016. С. 33-39.
- Ватутин Э. И., Титов В. С., Заикин О. С., Кочемазов С. Е., Валяев С. Ю., Журавлев А. Д., Манзюк М. О. Использование грид-систем для подсчета комбинаторных объектов на примере диагональных латинских квадратов порядка 9 // Информационные технологии и математическое моделирование систем 2016. М.: изд-во Центра информационных технологий в проектировании РАН, 2016. С. 154—157.
- Ватутин Э. И., Журавлев А. Д., Заикин О. С., Титов В. С. Учёт алгоритмических особенностей задачи при генерации диагональных латинских квадратов // Известия ЮЗГУ. 2016. № 2 (65). C. 46-59.
- Vatutin E.I., Zaikin O.S., Zhuravlev A.D., Manzyuk M.O., Kochemazov S.E., Titov V.S. Using grid systems for enumerating combinatorial objects on example of diagonal Latin squares // CEUR Workshop proceedings. Selected Papers of the 7th International Conference Distributed Computing and Grid-technologies in Science and Education. 2017. Vol. 1787. pp. 486–490. urn:nbn:de:0074-1787-5.
- О проекте Gerasim@home — Page 94 — Gerasim@home — Форум Boinc.ru (недоступная ссылка). Дата обращения: 22 ноября 2016. Архивировано 22 ноября 2016 года.
- Vatutin E.I., Kochemazov S.E., Zaikin O.S. Applying volunteer and parallel computing for enumerating diagonal Latin squares of order 9 // Proc. of The Eleventh International Conference on Parallel Computational Technologies, Vol. 753 of Communications in Computer and Information Science, Springer, 2017, pp. 114–129. DOI: 10.1007/978-3-319-67035-5_9.
- Vatutin E.I., Kochemazov S.E., Zaikin O.S., Valyaev S.Yu. Enumerating the Transversals for Diagonal Latin Squares of Small Order // CEUR Workshop Proceedings. Proceedings of the Third International Conference BOINC-based High Performance Computing: Fundamental Research and Development (BOINC:FAST 2017). Vol. 1973. Technical University of Aachen, Germany, 2017. pp. 6–14.
- Ватутин Э.И., Заикин О.С., Кочемазов С.Е., Валяев С.Ю., Титов В.С. Оценка числа трансверсалей для диагональных латинских квадратов // Телекоммуникации. 2018. № 1. С. 12–21.
- Vatutin E.I., Zaikin O.S., Kochemazov S.E., Valyaev S.Y. Using Volunteer Computing to Study Some Features of Diagonal Latin Squares // Open Engineering. Vol. 7. Iss. 1. 2017. pp. 453–460. DOI: 10.1515/eng-2017-0052.
- Vatutin E.I., Titov V.S., Zaikin O.S., Kochemazov S.E., Manzuk M.O., Nikitina N.N. Orthogonality-based classification of diagonal Latin squares of order 10 // CEUR Workshop Proceedings. Vol. 2267. Proceedings of the VIII International Conference "Distributed Computing and Grid-technologies in Science and Education" (GRID 2018). Dubna, JINR, 2018. pp. 282–287.
- Ватутин Э.И., Белышев А.Д., Кочемазов С.Е., Заикин О.С., Никитина Н.Н., Манзюк М.О. О полиномиальном сведении задач на базе латинских квадратов к задаче о точном покрытии // Оптико-электронные приборы и устройства в системах распознавания образов и обработки изображений (Распознавание – 2019). Курск: изд-во ЮЗГУ, 2019. С. 62–64.
- Vatutin E., Nikitina N., Belyshev A., Manzyuk M. On polynomial reduction of problems based on diagonal Latin squares to the exact cover problem // CEUR Workshop Proceedings. Proceedings of the Second International Conference Information, Computation, and Control Systems for Distributed Environments (ICCS-DE 2020). Vol. 2638. Technical University of Aachen, Germany, 2020.
- Vatutin E., Belyshev A., Kochemazov S., Zaikin O., Nikitina N. Enumeration of isotopy classes of diagonal Latin squares of small order using volunteer computing // Supercomputing Days Russia 2018. M.: Moscow State University, 2018. pp. 933–942.
- Vatutin E., Belyshev A., Kochemazov S., Zaikin O., Nikitina N. Enumeration of isotopy classes of diagonal Latin squares of small order using volunteer computing // Communications in Computer and Information Science. Vol. 965. Springer, 2018. pp. 578–586. DOI: 10.1007/978-3-030-05807-4_49.
- Ватутин Э.И., Кочемазов С.Е., Заикин О.С., Манзюк М.О., Никитина Н.Н., Титов В.С. О свойствах центральной симметрии диагональных латинских квадратов // Высокопроизводительные вычислительные системы и технологии. № 1 (8). 2018. С. 74–78.
- Vatutin E.I., Kochemazov S.E., Zaikin O.S., Manzuk M.O., Nikitina N.N., Titov V.S. Central Symmetry Properties for Diagonal Latin Squares // Problems of Information Technology. No. 2. 2019. pp. 3-8. DOI: 10.25045/jpit.v10.i2.01.
- Ватутин Э.И., Белышев А.Д. Определение числа самоортогональных (SODLS) и дважды самоортогональных диагональных латинских квадратов (DSODLS) порядков 1–10 // Высокопроизводительные вычислительные системы и технологии. Т. 4. № 1. 2020. С. 58–63.
- Ватутин Э.И., Титов В.С., Заикин О.С., Кочемазов С.Е., Манзюк М.О. Анализ комбинаторных структур на множестве отношения ортогональности диагональных латинских квадратов порядка 10 // Информационные технологии и математическое моделирование систем 2017. М.: ЦИТП РАН, 2017. С. 167–170.
- Vatutin E.I., Titov V.S., Zaikin O.S., Kochemazov S.E., Manzyuk M.O., Nikitina N.N. Orthogonality-based classification of diagonal Latin squares of order 10 // Distributed computing and grid-technologies in science and education (GRID’18): book of abstracts of the 8th international conference. Dubna: JINR, 2018. pp. 94–95.
- Zaikin O., Zhuravlev A., Kochemazov S., Vatutin E. On the Construction of Triples of Diagonal Latin Squares of Order 10 // Electronic Notes in Discrete Mathematics. Vol. 54C. 2016. pp. 307–312. DOI: 10.1016/j.endm.2016.09.053. (недоступная ссылка). Дата обращения: 28 мая 2019. Архивировано 22 ноября 2016 года.
Ссылки
- Официальный сайт проекта
- Твиттер проекта
- Ватутин Э. И., Титов В. С. Сравнение методов синтеза разбиений параллельных алгоритмов логического управления с использованием двухпараметрических диаграмм // Оптико-электронные приборы и устройства в системах распознавания образов, обработки изображений и символьной информации (Распознавание — 2012). Курск: изд-во ЮЗГУ, 2012. С. 138—140.
- Ватутин Э. И., Титов В. С. Сравнение методов синтеза разбиений граф-схем параллельных алгоритмов с использованием двумерных диаграмм // Известия ЮЗГУ. № 3 (42). Курск: изд-во ЮЗГУ, 2012. С. 66—74.
- Пленарный доклад «Использование грид-вычислений на платформе BOINC для построения разбиений параллельных алгоритмов логического управления» (Курск, 2012) на YouTube
- Ватутин Э. И., Титов В. С. Использование добровольных распределенных вычислений на платформе BOINC для анализа качества разбиений граф-схем параллельных алгоритмов // Параллельные вычисления и задачи управления (PACO’12). М.: ИПУ РАН, 2012.
- Ватутин Э. И., Титов В. С. Структурно-параметрическая оптимизация систем логического управления с использованием добровольных распределенных вычислений // Известия ЮЗГУ. Серия «Управление, вычислительная техника, информатика. Медицинское приборостроение». № 2. Ч. 1. С. 12-17. ISSN 2223—1536.
- Ватутин Э.И. Сравнение эвристических методов синтеза разбиений граф-схем параллельных алгоритмов с использованием добровольных распределенных вычислений на платформе BOINC // BOINC:FAST'13. Петрозаводск, 2013. на YouTube
- Научно-популярное описание задачи построения разбиений
- Ватутин Э. И., Валяев С. Ю. Расчетный модуль для построения разбиений параллельных алгоритмов логического управления с использованием добровольных распределенных вычислений // Свидетельство о государственной регистрации программы для ЭВМ № 2013618013 от 28.08.13.
- Vatutin E.I., Titov V.S. Voluntary distributed computing for solving discrete combinatorial optimization problems using Gerasim@home project // Distributed computing and grid-technologies in science and education: book of abstracts of the 6th international conference. Dubna: JINR, 2014. PP. 60-61. ISBN 978-5-9530-0387-2.
- Ватутин Э. И., Валяев С. Ю., Дремов Е. Н., Мартынов И. А., Титов В. С. Расчетный модуль для тестирования комбинаторных оптимизационных алгоритмов в задаче поиска кратчайшего пути в графе с использованием добровольных распределенных вычислений // Свидетельство о государственной регистрации программы для ЭВМ № 2014619797 от 22.09.14.
- Ватутин Э. И., Титов В. С. Анализ областей качественного превосходства последовательных эвристических методов синтеза разбиений при проектировании логических мультиконтроллеров // Известия высших учебных заведений. Приборостроение. 2015. Т. 58. № 2. С. 115—122. DOI: 10.17586/0021-3454-2015-58-2-115-122.
- Результаты вычислительных экспериментов в графическом виде
- Пленарный доклад «Решение задач дискретной комбинаторной оптимизации с использованием грид-систем на добровольной основе» (Курск, 2015) на YouTube
- Vatutin E.I., Valyaev S.Yu., Titov V.S. Comparison of Sequential Methods for Getting Separations of Parallel Logic Control Algorithms Using Volunteer Computing // CEUR Workshop Proceedings. Proceedings of the Second International Conference BOINC-based High Performance Computing: Fundamental Research and Development (BOINC:FAST 2015). Vol. 1502. Technical University of Aachen, Germany, 2015. P. 37-51. urn: nbn: de:0074-1502-3.
- Ватутин Э. И., Валяев С. Ю., Титов В. С. Анализ результатов применения метода случайного перебора при построении разбиений граф-схем параллельных алгоритмов в зависимости от размерности задачи и силы ограничений // Перспективные информационные технологии (ПИТ 2016). Самара: изд-во Самарского научного центра РАН, 2016. С. 481—486.
- Подсчет числа диагональных латинских квадратов с использованием добровольных распределенных вычислений
- Результаты проекта в графической форме (по состоянию на август 2017)
- Перечень различных комбинаторных структур из ДЛК порядка 1-8
- Перечень различных комбинаторных структур из ДЛК порядка 10, найденных в проекте
- Ватутин Э.И., Кочемазов С.Е., Заикин О.С., Цитерров И.И. Оценка вероятности нахождения ортогональных диагональных латинских квадратов среди диагональных латинских квадратов общего вида // Оптико-электронные приборы и устройства в системах распознавания образов, обработки изображений и символьной информации (Распознавание – 2018). Курск: изд-во ЮЗГУ, 2018. С. 72–74.
Обсуждение проекта в форумах: