Метод Эйлера — Паркера

Метод Эйлера — Паркера — метод построения ортогонального квадрата для заданного латинского квадрата порядка $N$ . Предложен Паркером в 1959 году[1].

Метод

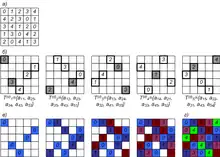
Пример диагонального латинского квадрата (а); множество его диагональных трансверсалей (б), элементы трансверсалей, лежащие на диагоналях, выделены серым; процесс построения ортогонального диагонального латинского квадрата из непересекающихся трансверсалей по методу Эйлера — Паркера (в).

Метод поиска состоит из трех шагов:

Построение множества трансверсалей заданного латинского квадрата.
Выбор из них подмножеств из $N$ непересекающихся трансверсалей.
Формирование ортогональных латинских квадратов из найденных подмножеств.

Построение трансверсалей и выбор непересекающихся подмножеств из них возможно реализовать с использованием метода полного перебора, однако более эффективной практической реализацией является полиномиальное сведение данных задач к задаче о точном покрытии, для решения которой эффективным является применение алгоритма танцующих связей (DLX).

При поиске ортогональных диагональных латинских квадратов вместо трансверсалей общего вида используются диагональные трансверсали, в состав которых входит по одному элементу с главной и побочной диагонали квадрата.

Формирование ортогонального квадрата из найденного подмножества из $N$ непересекающихся трансверсалей производится путем заполнения каждой $i$ -й трансверсали значением $i$ в формируемом ортогональном квадрате.

Историческая справка

Первая пара ортогональных латинских квадратов порядка 10, найденная Паркером в 1959 г.[1]

Леонардом Эйлером в ходе решения задачи о 36 офицерах была выдвинута гипотеза о том, что пары ортогональных латинских квадратов не существуют для всех размерностей $N=4t+2$ . Верность гипотезы для размерности $N=6$ была подтверждена Томасом Клаузеном в 1842 году. Поиск контрпримера к гипотезе Эйлера был осуществлен в 1957 году Пейджем и Томпкинсом с использованием метода полного перебора на компьютере SWAC, однако он не увенчался успехом ввиду необходимости огромных вычислительных затрат. В 1959 году Паркером[1] было предложено построение ортогонального квадрата с использованием трансверсалей и компьютера UNIVAC и был найден контрпример к гипотезе Эйлера для порядка $N=10$ . Аналогичный результат, опровергающий гипотезу Эйлера, был опубликован том же году в работе Бозе и Шринкхенде[2]. В 1992 году Брауном[3] описан диагональный латинский квадрат порядка 10, имеющий одновременно 4 ортогональных диагональных латинских квадрата, 3 из которых приведены в статье, а 4-й был найден О. Заикиным с использованием подхода на базе SAT. В настоящее время известны диагональные латинские квадраты порядка 10, имеющие 1, 2, 3, 4, 5, 6, 7, 8 и 10 нормализованных ортогональных диагональных латинских квадратов (последовательность A287695 в OEIS). Они формируют 42 комбинаторных структуры (графа из диагональных латинских квадратов на множестве бинарного отношения ортогональности)[4]. Большая часть из них была найдена в проекте добровольных распределенных вычислений Gerasim@Home начиная с 2017 г. Вопросы о существовании диагональных латинских квадратов порядка 10 с большим числом нормализованных ортогональных латинских квадратов и о существовании клики мощностью более двух из попарно ортогональных латинских квадратов порядка 10 в настоящее время являются открытыми.

См. также

Примечания

Parker E.T. Orthogonal Latin squares // Proc. Natl. Acad. Sci. USA. Vol. 45(6). 1959. pp. 859–862.
Bose R.C., Shrikhande S.S. On the falsity of Euler's conjecture about the non-existence of two orthogonal latin squares of order 4t + 2 // Proc Natl Acad Sci U S A. 1959 May; 45(5): 734–737.
Brown J.W., Cherry F., Most L., Most M., Parker E.T., Wallis W.D. Completion of the spectrum of orthogonal diagonal Latin squares // Lecture notes in pure and applied mathematics. 1992. Vol. 139. pp. 43–49.
Список комбинаторных структур из ДЛК порядка 10 на множестве отношения ортогональности

Литература

Кнут Д.Э. Искусство программирования. Т. 4А. Комбинаторные алгоритмы. Ч. 1. М.: Вильямс, 2013. 960 с.
Colbourn C.J., Dinitz J.H. Handbook of Combinatorial Designs, Second Edition. Chapman & Hall/CRC, 2006. 1016 p.
Keedwell A.D., Dénes J. Latin Squares and their Applications. Elsevier, 2015. 438 p. doi:10.1016/C2014-0-03412-0
Vatutin E., Nikitina N., Belyshev A., Manzyuk M. On polynomial reduction of problems based on diagonal Latin squares to the exact cover problem // CEUR Workshop Proceedings. Proceedings of the Second International Conference Information, Computation, and Control Systems for Distributed Environments (ICCS-DE 2020). Vol. 2638. Technical University of Aachen, Germany, 2020. urn:nbn:de:0074-2638-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Parker-1] Parker E.T. Orthogonal Latin squares // Proc. Natl. Acad. Sci. USA. Vol. 45(6). 1959. pp. 859–862.

[2] Bose R.C., Shrikhande S.S. On the falsity of Euler's conjecture about the non-existence of two orthogonal latin squares of order 4t + 2 // Proc Natl Acad Sci U S A. 1959 May; 45(5): 734–737.

[3] Brown J.W., Cherry F., Most L., Most M., Parker E.T., Wallis W.D. Completion of the spectrum of orthogonal diagonal Latin squares // Lecture notes in pure and applied mathematics. 1992. Vol. 139. pp. 43–49.

[4] Список комбинаторных структур из ДЛК порядка 10 на множестве отношения ортогональности