Сеть Фейстеля
Сеть Фе́йстеля, или конструкция Фейстеля (англ. Feistel network, Feistel cipher), — один из методов построения блочных шифров. Сеть состоит из ячеек, называемых ячейками Фейстеля. На вход каждой ячейки поступают данные и ключ. На выходе каждой ячейки получают изменённые данные и изменённый ключ. Все ячейки однотипны, и говорят, что сеть представляет собой определённую многократно повторяющуюся (итерированную) структуру. Ключ выбирается в зависимости от алгоритма шифрования/расшифрования и меняется при переходе от одной ячейки к другой. При шифровании и расшифровании выполняются одни и те же операции; отличается только порядок ключей. Ввиду простоты операций сеть Фейстеля легко реализовать как программно, так и аппаратно. Ряд блочных шифров (DES, RC2, RC5, RC6, Blowfish, FEAL, CAST-128, TEA, XTEA, XXTEA и др.) использует сеть Фейстеля в качестве основы. Альтернативой сети Фейстеля является подстановочно-перестановочная сеть (AES и др.).
История
В 1971 году Хорст Фейстель запатентовал два устройства, реализующие различные алгоритмы шифрования, позже получившие название «Люцифер» (англ. Lucifer). Одно из этих устройств использовало конструкцию, впоследствии названную «сетью Фейстеля» (англ. Feistel cipher, Feistel network). Тогда Фейстель работал над созданием новых криптосистем в стенах IBM вместе с Доном Копперсмитом. Проект «Люцифер» был скорее экспериментальным, но стал основой для алгоритма DES (англ. data encryption standard). В 1973 году журнал «Scientific American» опубликовал статью Фейстеля «Криптография и компьютерная безопасность» (англ. Cryptography and computer privacy)[1], в которой раскрыты некоторые важные аспекты шифрования и приведено описание первой версии проекта «Люцифер». В первой версии проекта «Люцифер» сеть Фейстеля не использовалась.
На основе сети Фейстеля был спроектирован алгоритм DES. В 1977 году власти США приняли стандарт FIPS 46-3, признающий DES стандартным методом шифрования данных. DES некоторое время широко использовался в криптографических системах. Итеративная структура алгоритма позволяла создавать простые программные и аппаратные реализации.
Согласно некоторым данным[2], в СССР уже в 1970-е годы КГБ разрабатывала блочный шифр, использовавший сеть Фейстеля, и, вероятно, именно этот шифр в 1990 году был принят в качестве ГОСТ 28147-89.
В 1987 году были разработаны алгоритмы FEAL и RC2. Сети Фейстеля получили широкое распространение в 1990-е годы — в годы появления таких алгоритмов, как Blowfish (1993), TEA (1994), RC5 (1994), CAST-128 (1996), XTEA (1997), XXTEA (1998), RC6 (1998) и других.
2 января 1997 года институт NIST объявил конкурс по созданию нового алгоритма шифрования данных, призванного заменить DES. Новый блочный шифр получил название AES (англ. advanced encryption standard) и был утверждён 26 мая 2002 года. В AES вместо сети Фейстеля используется подстановочно-перестановочная сеть.
Конструкция блочного шифра на основе сетей Фейстеля

Шифрование
Пусть требуется зашифровать некоторую информацию, представленную в двоичном виде (в виде последовательности нулей и единиц) и находящуюся в памяти компьютера или иного устройства (например, в файле).
Алгоритм шифрования.
- Информация разбивается на блоки одинаковой (фиксированной) длины. Полученные блоки называются входными, так как поступают на вход алгоритма. В случае если длина входного блока меньше, чем размер, который выбранный алгоритм шифрования способен зашифровать единовременно (размер блока), то блок удлиняется каким-либо способом. Как правило, длина блока является степенью двойки, например, составляет 64 бита или 128 бит.
Далее будем рассматривать операции, происходящие только с одним блоком, так как в процессе шифрования с другими блоками выполняются те же самые операции.
- Выбранный блок делится на два подблока одинакового размера — «левый» () и «правый» ().
- «Правый подблок» изменяется функцией F с использованием раундового ключа :
- Результат складывается по модулю 2 («xor») с «левым подблоком» :
- Результат будет использован в следующем раунде в роли «правого подблока» :
- «Правый подблок» текущего раунда (в своем не измененном на момент начала раунда виде) будет использован в следующем раунде в роли «левого подблока» :
- По какому-либо математическому правилу вычисляется раундовый ключ — ключ, который будет использоваться в следующем раунде.
Перечисленные операции выполняются N-1 раз, где N — количество раундов в выбранном алгоритме шифрования. При этом между переходами от одного раунда (этапа) к другому изменяются ключи: заменяется на , — на и т. д.).
Расшифрование
Расшифровка информации происходит так же, как и шифрование, с тем лишь исключением, что ключи следуют в обратном порядке, то есть не от первого к N-му, а от N-го к первому.
Алгоритмическое описание
- Блок открытого текста делится на две равные части: .
- В каждом раунде вычисляются:
- где:
- i — номер раунда;
- N — количество раундов в выбранном алгоритме шифрования;
- — некоторая функция;
- — ключ i-1-го раунда (раундовый ключ).
Результатом выполнения раундов является . В N-м раунде перестановка и не производится, чтобы была возможность использовать ту же процедуру и для расшифрования, просто инвертировав порядок использования ключей ( вместо ):
Небольшим изменением можно добиться и полной идентичности процедур шифрования и расшифрования.
Достоинства:
- обратимость алгоритма независимо от используемой функции f;
- возможность выбора сколь угодно сложной функции f.
Математическое описание
Рассмотрим пример. Пусть:
- X — блок данных, поступающий на вход (входной блок);
- A — некоторое инволютивное преобразование (или инволюция) — взаимно-однозначное преобразование, которое является обратным самому себе[3], то есть для каждого (∀) X справедливо выражение:
- Y — блок данных, получаемый на выходе (результат).
При однократном применении преобразования A к входному блоку X получится выходной блок Y:
При применении преобразования A к результату предыдущего преобразования — Y получится:
Пусть входной блок X состоит из двух подблоков L и R равной длины:
Определим два преобразования:
- — шифрование данных X с ключом K:
- — перестановка подблоков L и R:
Введём обозначения:
- однократное применение преобразования G:
- двукратное применение преобразования G:
Докажем инволютивность двукратного преобразования G ().
Несложно заметить, что преобразование G меняет только левый подблок L, оставляя правый R неизменным:
Поэтому далее будем рассматривать только подблок L. После двукратного применения преобразования G к L получим:
Таким образом:
следовательно
и G — инволюция.
Докажем инволютивность двукратного преобразования T ().
Рассмотрим процесс шифрования. Пусть:
- X — входное значение;
- — преобразование с ключом ;
- — выходное значение, результат i-го раунда.
Тогда преобразование, выполняемое на i+1-м раунде, можно записать в виде:
- .
Преобразование, выполняемое на 1-м раунде:
Следовательно, выходное значение после m раундов шифрования будет равно:
Можно заметить, что на последнем этапе не обязательно выполнять перестановку T.
Расшифрование ведётся применением всех преобразований в обратном порядке. В силу инволютивности каждого из преобразований обратный порядок даёт исходный результат:
Функции, используемые в сетях Фейстеля
В своей работе «Криптография и компьютерная безопасность»[1] Хорст Фейстель описывает два блока преобразований (функций ):
- блок подстановок (s-блок, англ. s-box);
- блок перестановок (p-блок, англ. p-box).
Можно показать, что любое двоичное преобразование над блоком данных фиксированной длины может быть реализовано в виде s-блока. В силу сложности строения N-разрядного s-блока при больших N на практике применяют более простые конструкции.
Термин «блок» в оригинальной статье[1] используется вместо термина «функция» вследствие того, что речь идёт о блочном шифре и предполагалось, что s- и p-блоки будут цифровыми микросхемами (цифровыми блоками).
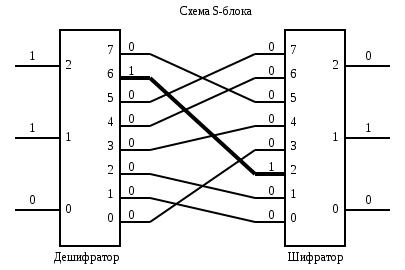
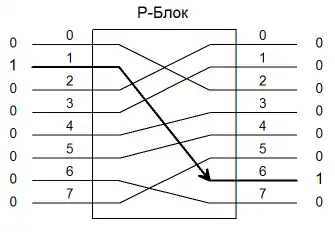
S-блок
Блок подстановок (s-блок, англ. s-box) состоит из следующих частей:
- дешифратор — преобразователь n-разрядного двоичного сигнала в одноразрядный сигнал по основанию ;
- система коммутаторов — внутренние соединения (всего возможных соединений );
- шифратор — преобразователь сигнала из одноразрядного -ричного в n-разрядный двоичный.
Анализ n-разрядного S-блока при большом n крайне сложен, однако реализовать такой блок на практике очень сложно, так как число возможных соединений крайне велико (). На практике блок подстановок используется как часть более сложных систем.
В общем случае s-блок может иметь несовпадающее число входов/выходов, в этом случае в системе коммутации от каждого выхода дешифратора может идти не строго одно соединение, а 2 или более или не идти вовсе. То же самое справедливо и для входов шифратора.
В электронике можно непосредственно применять приведённую справа схему. В программировании же генерируют таблицы замены. Оба этих подхода являются эквивалентными, то есть файл, зашифрованный на компьютере, можно расшифровать на электронном устройстве и наоборот.
| № комбинации | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Вход | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| Выход | 011 | 000 | 001 | 100 | 110 | 111 | 010 | 101 |
P-блок
Блок перестановок (p-блок, англ. p-box) всего лишь изменяет положение цифр и является линейным устройством. Этот блок может иметь очень большое количество входов-выходов, однако в силу линейности систему нельзя считать криптоустойчивой.
Криптоанализ ключа для n-разрядного p-блока проводится путём подачи на вход n-1 различных сообщений, каждое из которых состоит из n-1 нуля («0») и 1 единицы («1») (или наоборот, из единиц и нуля).
Циклический сдвиг
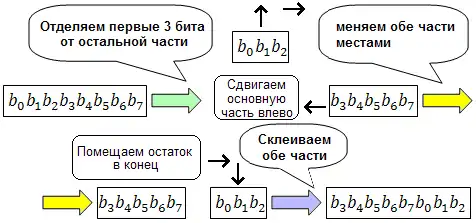
Можно показать, что циклический сдвиг является частным случаем p-блока.
В простейшем случае (сдвиг на 1 бит), крайний бит отщепляется и перемещается на другой конец регистра или шины. В зависимости от того какой бит берётся, правый или левый, сдвиг называется вправо или влево. Сдвиги на большее число бит можно рассматривать, как многократное применение сдвига на 1.
| Направление сдвига | Порядок следования битов до сдвига | Порядок следования битов после сдвига |
|---|---|---|
| Влево | ||
| Вправо |
Сложение по модулю n
Операция «сложение по модулю n» обозначается как
- (A + B) mod n
и представляет собой остаток от деления суммы A + B на n, где A и B — числа.
Можно показать, что сложение двух чисел по модулю n представляется в двоичной системе счисления в виде s-блока, у которого на вход подаётся число A, а в качестве системы коммутации s-блока используется циклический сдвиг влево на B разрядов.
В компьютерной технике и электронике операция сложения, как правило, реализована как сложение по модулю , где m — целое (обычно m равно разрядности машины). Для получения в двоичной системе
- A + B mod
достаточно сложить числа, после чего отбросить разряды начиная с m-го и старше.
Умножение по модулю n
Умножение по модулю n обозначается как
- (A * B) mod n
и представляет собой остаток от деления произведения A * B на n, где A и B — числа.
В персональных компьютерах на платформе x86 при перемножении двух m-разрядных чисел получается число разрядностью 2*m. Чтобы получить остаток от деления на , нужно отбросить m старших бит.
Пример реализации на языке Си
Общий вид алгоритма шифрования, использующего сеть Фейстеля:
/* Функция, выполняющая преобразование подблока с учётом значения ключа (по ключу).
Реализация зависит от выбранного алгоритма блочного шифрования. */
int f (
int subblock, /* преобразуемый подблок */
int key /* ключ */
); /* возвращаемое значение - преобразованный блок */
/* Функция, выполняющая шифрование открытого текста */
void crypt (
int * left, /* левый входной подблок */
int * right, /* правый входной подблок */
int rounds, /* количество раундов */
int * key /* массив ключей (по ключу на раунд) */
) {
int i, temp;
for ( i = 0; i < rounds; i++ )
{
temp = *right ^ f( *left, key[i] );
*right = *left;
*left = temp;
}
}
/* Функция, выполняющая расшифрование текста */
void decrypt (
int * left, /* левый зашифрованный подблок */
int * right, /* правый зашифрованный подблок */
int rounds, /* количество раундов */
int * key /* массив ключей (по ключу на раунд) */
) {
int i, temp;
for ( i = rounds - 1; i >= 0; i-- )
{
temp = *left ^ f( *right, key[i] );
*left = *right;
*right = temp;
}
}
Достоинства и недостатки
Достоинства:
- простота аппаратной реализации на современной электронной базе;
- простота программной реализации в силу того, что значительная часть функций поддерживается на аппаратном уровне в современных компьютерах (например, сложение по модулю 2 («xor»), сложение по модулю , умножение по модулю , и т. д.);
- хорошая изученность алгоритмов, построенных на основе сетей Фейстеля[4].
Недостатки:
- за один раунд шифруется только половина входного блока[5].
Теоретические исследования
Сети Фейстеля были широко изучены криптографами в силу их обширного распространения. В 1988 году Майкл Луби и Чарльз Ракофф провели исследования сети Фейстеля и доказали, что если раундовая функция является криптостойкой псевдослучайной, а используемые ключи независимы в каждом раунде, то 3 раундов будет достаточно для того, чтобы блочный шифр являлся псевдослучайной перестановкой, тогда как четырёх раундов будет достаточно для того, чтобы сделать сильную псевдослучайную перестановку.
«Псевдослучайной перестановкой» Люби и Ракофф назвали такую, которая устойчива к атаке с адаптивным выбором открытого текста, а «сильной псевдослучайной перестановкой» — псевдослучайную перестановку, устойчивую к атаке с использованием выбранного шифрованного текста.
Иногда в западной литературе сеть Фейстеля называют «Luby-Rackoff block cipher» в честь Люби и Ракоффа, которые проделали большой объём теоретических исследований в этой области.
В дальнейшем, в 1997 году Мони Наор и Омер Рейнголд предложили упрощённый вариант конструкции Люби — Ракоффа, состоящий из четырёх раундов. В этом варианте в качестве первого и последнего раунда используются две попарно-независимые перестановки. Два средних раунда конструкции Наора — Рейнголда идентичны раундам в конструкции Люби — Ракоффа[6].
Большинство же исследований посвящено изучению конкретных алгоритмов. Во многих блочных шифрах на основе сети Фейстеля были найдены те или иные уязвимости, однако в ряде случаев эти уязвимости являются чисто теоретическими и при нынешней производительности компьютеров использовать их на практике для взлома невозможно.
Модификации сети Фейстеля
При большом размере блоков шифрования (128 бит и более) реализация такой конструкции Фейстеля на 32-разрядных архитектурах может вызвать затруднения, поэтому применяются модифицированные варианты этой конструкции. Обычно используются сети с четырьмя ветвями. На рисунке показаны наиболее распространённые модификации. Также существуют схемы, в которых длины половинок и не совпадают. Такие сети называются несбалансированными.
- Модификации сети Фейстеля
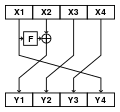
Тип 1 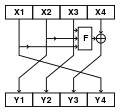
Тип 2 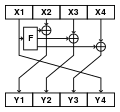
Тип 3
Алгоритм IDEA
Источник [7]:
| Схема одной итерации полного раунда алгоритма IDEA |
|---|
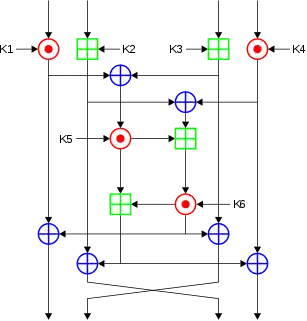 |
В алгоритме IDEA используется глубоко модифицированная сеть Фейстеля. В нём 64-битные входные блоки данных (обозначим за ) делятся на 4 подблока длиной 16 бит . На каждом этапе используется 6 16-битных ключей. Всего используется 8 основных этапов и 1 укороченный.
Формулы для вычисления значения подблоков на i-м раунде (для раундов c 1-го по 8-й):
- предварительные вычисления:
- финальные вычисления:
где — j-й ключ на i-м раунде.
Формула для вычисления 9-го раунда:
Выходом функции будет
Можно заметить, что s- и p-блоки в чистом виде не используются. В качестве основных операций используются:
- умножение по модулю ;
- сложение по модулю .
Шифры на основе сети Фейстеля
Люцифер (Lucifer)

Исторически первым алгоритмом, использующим сеть Фейстеля, был алгоритм «Люцифер», при работе над которым Фейстелем и была, собственно, разработана структура, впоследствии получившая название «сеть Фейстеля». В июне 1971 года Фейстелем был получен американский патент № 3798359[8].
Первая версия «Люцифера» использовала блоки и ключи длиной по 48 бит и не использовала конструкцию «сеть Фейстеля». Последующая модификация алгоритма была запатентована на имя Джона Л. Смитта (англ. John Lynn Smith) в ноябре 1971 года (US Patent 3,796,830; Nov 1971)[9], и в патенте содержится как описание собственно самой «сети Фейстеля», так и конкретной функции шифрования. В ней использовались 64-разрядные ключи и 32-битные блоки. И, наконец, последняя версия предложена в 1973 году и оперировала с 128-битными блоками и ключами. Наиболее полное описание алгоритма «Люцифер» было приведено в статье Артура Соркина (англ. Arthur Sorkin) «Люцифер. Криптографический алгоритм» («Lucifer, A Cryptographic Algorithm») в журнале «Криптология» («Cryptologia») за январь 1984[10].
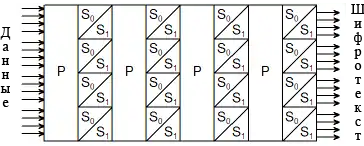
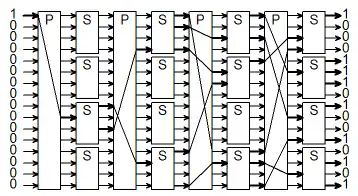
Хотя изначальная модификация «Люцифера» обходилась без «ячеек Фейстеля», она хорошо демонстрирует то, как только применением s- и p-блоков можно сильно исказить исходный текст. Структура алгоритма «Люцифер» образца июня 1971 года представляет собой «сэндвич» из слоёв двух типов, используемых по очереди — так называемые SP-сети (или подстановочно-перестановочные сети). Первый тип слоя — p-блок разрядности 128 бит, за ним идёт второй слой, представляющий собой 32 модуля, каждый из которых состоит их двух четырёхбитных s-блоков, чьи соответствующие входы закорочены и на них подаётся одно и то же значение с выхода предыдущего слоя. Но сами блоки подстановок различны (отличаются таблицами замен). На выход модуля подаются значения только с одного из s-блоков, какого конкретно — определяется одним из битов в ключе, номер которого соответствовал номеру s-блока в структуре. Упрощённая схема алгоритма меньшей разрядности и неполным числом раундов приведена на рисунке. В ней используется 16 модулей выбора s-блоков (всего 32 s-блока), таким образом такая схема использует 16-битный ключ.
Рассмотрим теперь, как будет меняться шифротекст, в приведённом выше алгоритме, при изменении всего одного бита. Для простоты возьмём таблицы замен s-блоков такими, что если на вход s-блока подаются все нули, то и на выходе будут все нули. В силу нашего выбора s-блоков, если на вход шифрующего устройства подаются все нули, то и на выходе устройства будут все нули. В реальных системах такие таблицы замен не используются, так как они сильно упрощают работу криптоаналитика, но в нашем примере они наглядно иллюстрируют сильную межсимвольную взаимосвязь при изменении одного бита шифруемого сообщения. Видно, что благодаря первому p-блоку единственная единица сдвигается перемещается в центр блока, затем следующий нелинейный s-блок «размножает» её, и уже две единицы за счёт следующего p-блока изменяют своё положение и т. д. В конце устройства шифрования, благодаря сильной межсимвольной связи, выходные биты стали сложной функцией от входных и от используемого ключа. В среднем на выходе половина бит будет равна «0» и половина — «1».
По своей сути сеть Фейстеля является альтернативой сложным SP-сетям и используется намного шире. С теоретической точки зрения раундовая функция шифрования может быть сведена к SP-сети, однако сеть Фейстеля является более практичной, так как шифрование и дешифрование может вестись одним и тем же устройством, но с обратным порядком используемых ключей. Вторая и третья версия алгоритма (использующие сеть Фейстеля) оперировали над 32-битными блоками с 64-битным ключом и 128-битными блоками со 128-битными ключами. В последней (третьей) версии раундовая функция шифрования была устроена очень просто — сначала шифруемый подблок пропускался через слой 4-битных s-блоков (аналогично слоям в SP-сетях, только s-блок является константным и не зависит от ключа), затем к нему по модулю 2 добавлялся раундовый ключ, после чего результат пропускался через p-блок.
DES
Функция (где:
- — 32-разрядный входной блок на i-й итерации;
- — 48-разрядный ключ на данной итерации)
в алгоритме DES состоит из следующих операций:
- расширение входного блока L до 48 разрядов (некоторые входные разряды могут повторяться);
- Сложение по модулю 2 с ключом :
- деление результата на 8 блоков длиной по 6 бит каждый:
- полученные блоки информации подаются на блоки подстановок, имеющие 6-разрядные входы и 4-разрядные выходы;
- на выходе 4-битные блоки объединяются в 32-битный, который и является результатом функции .
Полное число раундов в алгоритме DES равно 16.
«Магма»
Функция (где и — 32-битные числа) вычисляется следующим образом:
- складываются и по модулю :
- результат разбивается на 8 4-битных блоков, которые подаются на вход 4-разрядных s-блоков (которые могут быть различными);
- выходы s-блоков объединяют в 32-битное число, которое затем сдвигается циклически на 11 битов влево;
- полученный результат является выходом функции.
Количество раундов в алгоритме ГОСТ 28147—89 равно 32.
Сравнительный список алгоритмов
Следующие блочные шифры в качестве своей основы используют классическую или модифицированную сеть Фейстеля.
| Алгоритм | Год | Число раундов | Длина ключа | Размер блока | Количество подблоков |
|---|---|---|---|---|---|
| Blowfish | 1993 | 16 | от 32 до 448 | 64 | 2 |
| Camellia | 2000 | 18/24 | 128/192/256 | 128 | 2 |
| CAST-128 | 1996 | 12/16 | 40-128 | 64 | 2 |
| CAST-256 | 1998 | 12×4=48 | 128/192/256 | 128 | 2 |
| CIPHERUNICORN-A | 2000 | 16 | 128/192/256 | 128 | 2 |
| CIPHERUNICORN-E | 1998 | 16 | 128 | 64 | 2 |
| CLEFIA | 2007 | 16 | 128/192/256 | 128 | 16 |
| DEAL | 1998 | 6 (8) | (128/192) 256 | 128 | 2 |
| DES | 1977 | 16 | 56 | 64 | 2 |
| DFC | 1998 | 8 | 128/192/256 | 128 | ? |
| FEAL | 1987 | 4-32 | 64 | 64 | 2 |
| ГОСТ 28147-89 | 1989[2] | 32/16 | 256 | 64 | 2 |
| IDEA | 1991 | 8+1 | 128 | 64 | 4 |
| KASUMI | 1999 | 8 | 128 | 64 | 2 |
| Khufu | 1990 | 16-32/64 | 512 | 64 | 2 |
| LOKI97 | 1997 | 16 | 128/192/256 | 128 | 2 |
| Lucifer | 1971 | 16 | 48/64/128 | 48/32/128 | 2 |
| MacGuffin | 1994 | 32 | 128 | 64 | 4 |
| MAGENTA | 1998 | 6/8 | 128/192/256 | 128 | 2 |
| MARS | 1998 | 32 | 128—1248 | 128 | 2 |
| Mercy | 2000 | 6 | 128 | 4096 | ? |
| MISTY1 | 1995 | 4×n(8) | 128 | 64 | 4 |
| Raiden | 2006 | 16 | 128 | 64 | 2 |
| RC2 | 1987 | 16+2 | 8-128 | 64 | 4 |
| RC5 | 1994 | 1-255(12) | 0-2040(128) | 32/64/128 | 2 |
| RC6 | 1998 | 20 | 128/192/256 | 128 | 4 |
| RTEA | 2007 | 48/64 | 128/256 | 64 | 2 |
| SEED | 1998 | 16 | 128 | 128 | 2 |
| Sinople | 2003 | 64 | 128 | 128 | 4 |
| Skipjack | 1998 | 32 | 80 | 64 | 4 |
| TEA | 1994 | 64 | 128 | 64 | 2 |
| Triple DES | 1978 | 32/48 | 112/168 | 64 | 2 |
| Twofish | 1998 | 16 | 128/192/256 | 128 | 4 |
| XTEA | 1997 | 64 | 128 | 64 | 2 |
| XTEA-3 | 1999 | 64 | 256 | 128 | 4 |
| XXTEA | 1998 | 12-64 | 128 | 64 | 2 |
Примечания
- Хорст Фейстель «Cryptography and computer privacy» (англ.) («Криптография и компьютерная безопасность»). Перевод Андрея Винокурова.
- Винокуров А. Статья «Алгоритм шифрования ГОСТ 28147-89, его использование и реализация для компьютеров платформы Intel x86». Часть материалов, вошедших в данную статью, была опубликована в выпуске «#1,5/1995 год» журнала «Монитор».
- Дискретная математика. Алгоритмы. Симметричные системы и блочные шифры (недоступная ссылка). Дата обращения: 21 ноября 2008. Архивировано 5 декабря 2012 года.
- Сергей Панасенко. «Современные алгоритмы шифрования» // Журнал «Byte». Выпуск № 8 (60), август 2003.
- Баричев, Гончаров, Серов, 2011.
- On the construction of pseudo-random permutation: Luby-Rackoff revisited.
- Menezes, Oorschot, Vanstone, 1996, §7.6 IDEA, pp. 263.
- U.S. Patent 3 798 359
- U.S. Patent 3 796 830
- Arthur Sorkin. Lucifer, A Cryptographic Algorithm. Cryptologia, Выпуск 8(1), Январь 1984, стр. 22—41, с дополнением в выпуске 8(3), стр. 260—261
Литература
- Баричев С. Г., Гончаров В. В., Серов Р. Е. Основы современной криптографии — 3-е изд. — М.: Диалог-МИФИ, 2011. — 176 с. — ISBN 978-5-9912-0182-7
- Menezes A. J., Oorschot P. v., Vanstone S. A. Handbook of Applied Cryptography (англ.) — CRC Press, 1996. — 816 p. — (Discrete Mathematics and Its Applications) — ISBN 978-0-8493-8523-0
