Serpent

Алгоритм создавался под лозунгом «криптографический алгоритм 21 века» для участия в конкурсе AES. При создании нового алгоритма Serpent его авторы придерживались консервативных взглядов на проектирование, что подтверждается первоначальным решением об использовании таблиц подстановок из известного много лет ранее алгоритма шифрования DES, который в течение долгого времени изучался ведущими специалистами в области криптографии и защиты информации и чьи свойства и особенности были хорошо известны научному миру. Одновременно с этим к новому алгоритму мог быть применен исчерпывающий анализ, уже разработанный для DES. Не использовались новые, непроверенные и неиспытанные технологии при создании шифра, который в случае принятия был бы использован для защиты огромных массивов финансовых транзакций и правительственной информации. Основным требованием к участникам конкурса AES было то, что алгоритм-претендент должен быть быстрее, чем 3DES, и предоставлять как минимум такой же уровень безопасности: он должен иметь блок данных длиной 128 бит и ключ длиной 256 бит. 16-раундовый Serpent был бы таким же надежным, как 3DES, но в два раза быстрее. Однако, авторы посчитали, что для большей надежности стоит увеличить количество раундов до 32. Это сделало шифр таким же быстрым, как DES, и намного более надежным, чем 3DES.

Алгоритм Serpent представляет собой SP-сеть, в которой весь блок данных длиной 128 бит на каждом раунде разбивается на 4 слова длиной по 32 бита. Все значения, использующиеся при шифровании, представляются битовыми потоками. Индексы бит пробегают значения от 0 до 31 для 32-битных слов, от 0 до 127 для 128-битных блоков, от 0 до 255 для 256-битных ключей и так далее. Для внутренних вычислений все биты величин представлены в прямом порядке (little-endian).

Serpent шифрует открытый текст P длиной 128 бит в шифротекст C длиной так же 128 бит за 32 раунда с помощью 33 подключей ${\displaystyle K_{0},...,K_{32}}$ длиной 128 бит. Длина используемого ключа может принимать различные значения, но для конкретики зафиксируем их длину в 128, 192 или 256 бит. Короткие ключи длиной менее 256 бит дополняются до полной длины в 256 бит.

Шифрование состоит из следующих основных шагов:

• начальная перестановка;
• 32 раунда, каждый из которых состоит из операции смешивания с 128-битным ключом (побитовое логическое исключающее «или»), табличная замена (S-box) и линейное преобразование. В последнем раунде линейное преобразование заменяется дополнительным наложением ключа;
• конечная перестановка;

Начальная и конечная перестановки не имеют какой-либо криптографической значимости. Они используются для упрощения оптимизированной реализации алгоритма и повышения вычислительной эффективности.

Уравнения структуры алгоритма шифрования:

${\displaystyle {\hat {B}}_{0}=IP(P)}$

${\displaystyle {\hat {B}}_{i+1}=Re_{i}({\hat {B}}_{i})}$

${\displaystyle C=FP({\hat {B}}_{32})}$,

где

${\displaystyle Re_{i}(X)=L({\hat {S}}_{i}(X\oplus {\hat {K}}_{i})),i=0,...,30}$

${\displaystyle Re_{i}(X)={\hat {S}}_{i}(X\oplus {\hat {K}}_{i})\oplus {\hat {K}}_{32},i=31}$,

Уравнения структуры алгоритма расшифрования:

${\displaystyle {\hat {B}}_{0}=IP(P)}$

${\displaystyle {\hat {B}}_{i+1}=Rd_{31-i}({\hat {B}}_{i})}$

${\displaystyle C=FP({\hat {B}}_{32})}$,

где

${\displaystyle Rd_{i}(X)={\hat {S}}_{i}(X\oplus {\hat {K}}_{32})\oplus {\hat {K}}_{i},i=31}$,

${\displaystyle Rd_{i}(X)={\hat {S}}_{i}(L(X))\oplus {\hat {K}}_{i},i=30,...,0}$

где ${\displaystyle Re,Rd}$ - раундовые функции шифрования и расшифрования соответственно, ${\displaystyle {\hat {S}}_{i}}$ — это применение таблицы подстановки ${\displaystyle {\hat {S}}_{imod8}}$ 32 раз параллельно и ${\displaystyle L}$ — линейное преобразование.

Расшифрование отличается от шифрования только тем, что должны быть использованы инверсные (обратные) таблицы замен, а также обратные линейные преобразования, но только для раундовой функции R. Ключи подаются в обратном порядке. Битовые операции раундовой функции расшифрования (в т. ч. замены и перестановки) должны проходить в порядке обратном порядку битовых операций раундовой функции шифрования.

Как и другие алгоритмы, участвовавшие в конкурсе AES, Serpent имеет возможные длины ключа 128, 192 или 256 бит. «Неполный» ключ длиной меньше 256 бит дополняется по следующему правилу: прибавляется единичный бит справа, за ним следует столько нулевых битов, чтобы длина ключа стала равна 256 битам.

Сначала при необходимости ключ дополняется до 256 бит и преобразуется в 33 подключа ${\displaystyle K_{0},...,K_{32}}$ длиной 128 бит следующим способом:

Исходный ключ представляется в виде 8 32-битных слов ${\displaystyle w_{-8},...,w_{-1}}$ для вычисления промежуточного ключа по правилу:

${\displaystyle w_{i}=(w_{i-8}\oplus w_{i-5}\oplus w_{i-3}\oplus w_{i-1}\oplus \phi \oplus i)<<<11}$,

где ${\displaystyle \phi }$ — это дробная часть золотого сечения ${\displaystyle {\frac {{\sqrt {5}}+1}{2}}}$ или 0x9e3779b9 в шестнадцатеричной системе счисления, а ${\displaystyle <<<}$ — это циклический битовый сдвиг.

Раундовые ключи вычисляются из промежуточных ключей использованием таблиц подстановок следующим образом:

${\displaystyle \left\{k_{0},k_{1},k_{2},k_{3}\right\}=S_{3}\left(w_{0},w_{1},w_{2},w_{3}\right)}$

${\displaystyle \left\{k_{4},k_{5},k_{6},k_{7}\right\}=S_{2}\left(w_{4},w_{5},w_{6},w_{7}\right)}$

${\displaystyle \left\{k_{8},k_{9},k_{10},k_{11}\right\}=S_{1}\left(w_{8},w_{9},w_{10},w_{11}\right)}$

${\displaystyle \left\{k_{12},k_{13},k_{14},k_{15}\right\}=S_{0}\left(w_{12},w_{13},w_{14},w_{15}\right)}$

${\displaystyle \left\{k_{16},k_{17},k_{18},k_{19}\right\}=S_{7}\left(w_{16},w_{17},w_{18},w_{19}\right)}$

${\displaystyle \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots }$

${\displaystyle \left\{k_{124},k_{125},k_{126},k_{127}\right\}=S_{4}\left(w_{124},w_{125},w_{126},w_{127}\right)}$

${\displaystyle \left\{k_{128},k_{129},k_{130},k_{131}\right\}=S_{3}\left(w_{128},w_{129},w_{130},w_{131}\right)}$

Промежуточные 32-битные величины ${\displaystyle k_{j}}$ перенумеровываются и получаются 128-битные подключи:

${\displaystyle K_{i}=\left\{k_{4i},k_{4i+1},k_{4i+2},k_{4i+3}\right\}}$

При стандартном описании алгоритма мы должны применить начальную перестановку ${\displaystyle IP}$ к раундовому ключу, чтобы расположить биты ключа в надлежащем порядке, то есть ${\displaystyle {\hat {K}}_{i}=IP(K_{i})}$

Данная перестановка ${\displaystyle IP}$ задается следующей таблицей, где указывается позиция, на которую перейдет соответствующий бит (например, 32-й бит перейдет на 1-ю позицию):

Начальная перестановка ${\displaystyle IP}$

0	32	64	96	1	33	65	97	2	34	66	98	3	35	67	99
4	36	68	100	5	37	69	101	6	38	70	102	7	39	71	103
8	40	72	104	9	41	73	105	10	42	74	106	11	43	75	107
12	44	76	108	13	45	77	109	14	46	78	110	15	47	79	111
16	48	80	112	17	49	81	113	18	50	82	114	19	51	83	115
20	52	84	116	21	53	85	117	22	54	86	118	23	55	87	119
24	56	88	120	25	57	89	121	26	58	90	122	27	59	91	123
28	60	92	124	29	61	93	125	30	62	94	126	31	63	95	127

В алгоритме Serpent таблицы замен являются 4-битовыми перестановками со свойствами стойкости к дифференциальному криптоанализу, к линейному криптоанализу и тем свойством, что порядок выходных бит, как функции входных должен быть максимален, то есть быть равным 3.

Таблица подстановок генерируется из известных и хорошо изученных таблиц для алгоритма DES в итерационном процессе, пока не будут получены желаемые дифференциальные и линейные свойства. Таким образом, создается 8 таблиц подстановок.

Ниже представлены таблицы подстановок:

Таблица подстановок ${\displaystyle S_{i}}$

S0:	3	8	15	1	10	6	5	11	14	13	4	2	7	0	9	12
S1:	15	12	2	7	9	0	5	10	1	11	14	8	6	13	3	4
S2:	8	6	7	9	3	12	10	15	13	1	14	4	0	11	5	2
S3:	0	15	11	8	12	9	6	3	13	1	2	4	10	7	5	14
S4:	1	15	8	3	12	0	11	6	2	5	4	10	9	14	7	13
S5:	15	5	2	11	4	10	9	12	0	3	14	8	13	6	7	1
S6:	7	2	12	5	8	4	6	11	14	9	1	15	13	3	10	0
S7:	1	13	15	0	14	8	2	11	7	4	12	10	9	3	5	6

И инверсные таблицы подстановок:

Таблица инверсных подстановок ${\displaystyle S_{i}^{-1}}$

InvS0:	13	3	11	0	10	6	5	12	1	14	4	7	15	9	8	2
InvS1:	5	8	2	14	15	6	12	3	11	4	7	9	1	13	10	0
InvS2:	12	9	15	4	11	14	1	2	0	3	6	13	5	8	10	7
InvS3:	0	9	10	7	11	14	6	13	3	5	12	2	4	8	15	1
InvS4:	5	0	8	3	10	9	7	14	2	12	11	6	4	15	13	1
InvS5:	8	15	2	9	4	1	13	14	11	6	5	3	7	12	10	0
InvS6:	15	10	1	13	5	3	6	0	4	9	14	7	2	12	8	11
InvS7:	3	0	6	13	9	14	15	8	5	12	11	7	10	1	4	2

Линейное преобразование ${\displaystyle LT}$ задается следующей таблицей, где биты перечислены от 0 до 127 (например, выходной 2 бит образован 2, 9, 15, 30, 76, 84, 126 битами, сложенными по модулю 2). В каждой строке описывается 4 выходных бита, которые вместе составляют входные данные на одну таблицу замен в следующем раунде. Стоит отметить, что данный набор представляет собой таблицу ${\displaystyle IP(LT(FP(x)))}$, где ${\displaystyle LT}$ и есть то линейное преобразование.

Таблица линейного преобразования:

Линейное преобразование ${\displaystyle LT}$

{16 52 56 70 83 94 105}	{72 114 125}	{ 2 9 15 30 76 84 126}	{36 90 103}
{20 56 60 74 87 98 109}	{ 1 76 118}	{ 2 6 13 19 34 80 88}	{40 94 107}
{24 60 64 78 91 102 113}	{ 5 80 122}	{ 6 10 17 23 38 84 92}	{44 98 111}
{28 64 68 82 95 106 117}	{ 9 84 126}	{10 14 21 27 42 88 96}	{48 102 115}
{32 68 72 86 99 110 121}	{ 2 13 88}	{14 18 25 31 46 92 100}	{52 106 119}
{36 72 76 90 103 114 125}	{ 6 17 92}	{18 22 29 35 50 96 104}	{56 110 123}
{ 1 40 76 80 94 107 118}	{10 21 96}	{22 26 33 39 54 100 108}	{60 114 127}
{ 5 44 80 84 98 111 122}	{14 25 100}	{26 30 37 43 58 104 112}	{ 3 118 }
{ 9 48 84 88 102 115 126}	{18 29 104}	{30 34 41 47 62 108 116}	{ 7 122 }
{ 2 13 52 88 92 106 119}	{22 33 108}	{34 38 45 51 66 112 120}	{11 126 }
{ 6 17 56 92 96 110 123}	{26 37 112}	{38 42 49 55 70 116 124}	{ 2 15 76}
{10 21 60 96 100 114 127}	{30 41 116}	{ 0 42 46 53 59 74 120}	{ 6 19 80}
{ 3 14 25 100 104 118 }	{34 45 120}	{ 4 46 50 57 63 78 124}	{10 23 84}
{ 7 18 29 104 108 122 }	{38 49 124}	{ 0 8 50 54 61 67 82}	{14 27 88}
{11 22 33 108 112 126 }	{ 0 42 53}	{ 4 12 54 58 65 71 86}	{18 31 92}
{ 2 15 26 37 76 112 116}	{ 4 46 57}	{ 8 16 58 62 69 75 90}	{22 35 96}
{ 6 19 30 41 80 116 120}	{ 8 50 61}	{12 20 62 66 73 79 94}	{26 39 100}
{10 23 34 45 84 120 124}	{12 54 65}	{16 24 66 70 77 83 98}	{30 43 104}
{ 0 14 27 38 49 88 124}	{16 58 69}	{20 28 70 74 81 87 102}	{34 47 108}
{ 0 4 18 31 42 53 92}	{20 62 73}	{24 32 74 78 85 91 106}	{38 51 112}
{ 4 8 22 35 46 57 96}	{24 66 77}	{28 36 78 82 89 95 110}	{42 55 116}
{ 8 12 26 39 50 61 100}	{28 70 81}	{32 40 82 86 93 99 114}	{46 59 120}
{12 16 30 43 54 65 104}	{32 74 85}	{36 90 103 118 }	{50 63 124}
{16 20 34 47 58 69 108}	{36 78 89}	{40 94 107 122 }	{ 0 54 67}
{20 24 38 51 62 73 112}	{40 82 93}	{44 98 111 126 }	{ 4 58 71}
{24 28 42 55 66 77 116}	{44 86 97}	{ 2 48 102 115 }	{ 8 62 75}
{28 32 46 59 70 81 120}	{48 90 101}	{ 6 52 106 119 }	{12 66 79}
{32 36 50 63 74 85 124}	{52 94 105}	{10 56 110 123 }	{16 70 83}
{ 0 36 40 54 67 78 89}	{56 98 109}	{14 60 114 127 }	{20 74 87}
{ 4 40 44 58 71 82 93}	{60 102 113}	{ 3 18 72 114 118 125 }	{24 78 91}
{ 8 44 48 62 75 86 97}	{64 106 117}	{ 1 7 22 76 118 122 }	{28 82 95}
{12 48 52 66 79 90 101}	{68 110 121}	{ 5 11 26 80 122 126 }	{32 86 99}

Таблица обратного линейного преобразования, которое используется при расшифровке:

Обратное линейное преобразование ${\displaystyle ILT}$

{ 53 55 72}	{ 1 5 20 90 }	{ 15 102}	{ 3 31 90 }
{ 57 59 76}	{ 5 9 24 94 }	{ 19 106}	{ 7 35 94 }
{ 61 63 80}	{ 9 13 28 98 }	{ 23 110}	{11 39 98 }
{ 65 67 84}	{13 17 32 102 }	{ 27 114}	{ 1 3 15 20 43 102 }
{ 69 71 88}	{17 21 36 106 }	{ 1 31 118}	{ 5 7 19 24 47 106 }
{ 73 75 92}	{21 25 40 110 }	{ 5 35 122}	{ 9 11 23 28 51 110 }
{ 77 79 96}	{25 29 44 114 }	{ 9 39 126}	{13 15 27 32 55 114 }
{ 81 83 100}	{ 1 29 33 48 118}	{ 2 13 43}	{ 1 17 19 31 36 59 118}
{ 85 87 104}	{ 5 33 37 52 122}	{ 6 17 47}	{ 5 21 23 35 40 63 122}
{ 89 91 108}	{ 9 37 41 56 126}	{10 21 51}	{ 9 25 27 39 44 67 126}
{ 93 95 112}	{ 2 13 41 45 60}	{14 25 55}	{ 2 13 29 31 43 48 71}
{ 97 99 116}	{ 6 17 45 49 64}	{18 29 59}	{ 6 17 33 35 47 52 75}
{101 103 120}	{10 21 49 53 68}	{22 33 63}	{10 21 37 39 51 56 79}
{105 107 124}	{14 25 53 57 72}	{26 37 67}	{14 25 41 43 55 60 83}
{ 0 109 111}	{18 29 57 61 76}	{30 41 71}	{18 29 45 47 59 64 87}
{ 4 113 115}	{22 33 61 65 80}	{34 45 75}	{22 33 49 51 63 68 91}
{ 8 117 119}	{26 37 65 69 84}	{38 49 79}	{26 37 53 55 67 72 95}
{ 12 121 123}	{30 41 69 73 88}	{42 53 83}	{30 41 57 59 71 76 99}
{ 16 125 127}	{34 45 73 77 92}	{46 57 87}	{34 45 61 63 75 80 103}
{ 1 3 20}	{38 49 77 81 96}	{50 61 91}	{38 49 65 67 79 84 107}
{ 5 7 24}	{42 53 81 85 100}	{54 65 95}	{42 53 69 71 83 88 111}
{ 9 11 28}	{46 57 85 89 104}	{58 69 99}	{46 57 73 75 87 92 115}
{ 13 15 32}	{50 61 89 93 108}	{62 73 103}	{50 61 77 79 91 96 119}
{ 17 19 36}	{54 65 93 97 112}	{66 77 107}	{54 65 81 83 95 100 123}
{ 21 23 40}	{58 69 97 101 116}	{70 81 111}	{58 69 85 87 99 104 127}
{ 25 27 44}	{62 73 101 105 120}	{74 85 115}	{ 3 62 73 89 91 103 108}
{ 29 31 48}	{66 77 105 109 124}	{78 89 119}	{ 7 66 77 93 95 107 112}
{ 33 35 52}	{ 0 70 81 109 113}	{82 93 123}	{11 70 81 97 99 111 116}
{ 37 39 56}	{ 4 74 85 113 117}	{86 97 127}	{15 74 85 101 103 115 120}
{ 41 43 60}	{ 8 78 89 117 121}	{ 3 90}	{19 78 89 105 107 119 124}
{ 45 47 64}	{12 82 93 121 125}	{ 7 94}	{ 0 23 82 93 109 111 123}
{ 49 51 68}	{ 1 16 86 97 125}	{ 11 98}	{ 4 27 86 97 113 115 127}

Данная перестановка является обратной к начальной, то есть ${\displaystyle FP=IP^{-1}}$, и задается следующей таблицей:

Конечная перестановка ${\displaystyle FP}$

0	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60
64	68	72	76	80	84	88	92	96	100	104	108	112	116	120	124
1	5	9	13	17	21	25	29	33	37	41	45	49	53	57	61
65	69	73	77	81	85	89	93	97	101	105	109	113	117	121	125
2	6	10	14	18	22	26	30	34	38	42	46	50	54	58	62
66	70	74	78	82	86	90	94	98	102	106	110	114	118	122	126
3	7	11	15	19	23	27	31	35	39	43	47	51	55	59	63
67	71	75	79	83	87	91	95	99	103	107	111	115	119	123	127

Эффективная реализация алгоритма

Желание авторов сделать алгоритм именно таким, какой он есть, становится понятным при рассмотрении его эффективной низкоуровневой реализации.

Serpent был создан таким образом, чтобы все операции в процессе шифрования и расшифрования одного блока могли быть выполнены параллельно в 32 потока. К тому же низкоуровневое описание алгоритма намного проще, чем стандартное описание. Никаких начальных и конечных перестановок не требуется.

Шифрование состоит из 32 раундов. Открытый текст является первыми промежуточными данными ${\displaystyle B_{0}=P}$. Затем выполняется 32 раунда, каждый i раунд состоит из:

• смешивания с ключом. Производится побитовое исключающее «или» промежуточных данных ${\displaystyle B_{i}}$ с ключом длиной 128 бит;
• применение таблиц подстановок. Входные данные длиной 128 бит разделяются на 4 слова по 32 бита. Таблица подстановок, реализованная последовательностью логических операций (как если это было бы реализовано аппаратно), применяется к этим 4 словам. В результате получается 4 выходных слова. Таким образом, центральный процессор выполняет подстановку по 32 копиям таблицы одновременно;
• линейное преобразование.

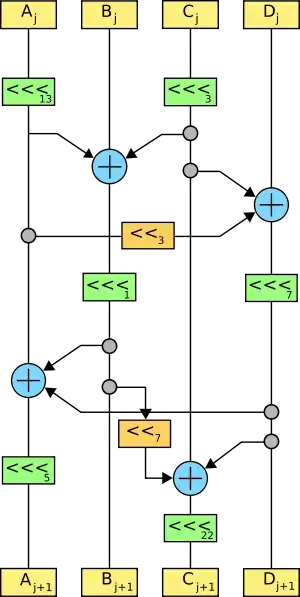
32-битные слова преобразуются следующим образом:

${\displaystyle X_{0},X_{1},X_{2},X_{3}=S_{i}(B_{i}\oplus K_{i})}$

${\displaystyle X_{0}=X_{0}<<<13}$

${\displaystyle X_{2}=X_{2}<<<3}$

${\displaystyle X_{1}=X_{1}\oplus X_{0}\oplus X2}$

${\displaystyle X_{3}=X_{3}\oplus X_{2}\oplus (X_{0}<<3)}$

${\displaystyle X_{1}=X_{1}<<<1}$

${\displaystyle X_{3}=X_{3}<<<7}$

${\displaystyle X_{0}=X_{0}\oplus X_{1}\oplus X3}$

${\displaystyle X_{2}=X_{2}\oplus X_{3}\oplus (X_{1}<<7)}$

${\displaystyle X_{0}=X_{0}<<<5}$

${\displaystyle X_{2}=X_{2}<<<22}$

${\displaystyle B_{i+1}=X_{0},X_{1},X_{2},X_{3}}$,

где ${\displaystyle <<<}$ обозначает циклический битовый сдвиг, а ${\displaystyle <<}$ — битовый сдвиг. В последнем раунде это линейное преобразование заменено дополнительным смешиванием с ключом ${\displaystyle B_{32}=S_{7}(B_{31}\oplus K_{31})\oplus K_{32}}$

Первой причиной выбора такого линейного преобразования является максимизация лавинного эффекта. Такие таблицы подстановок имеют свойство, что изменение каждого входного бита приведет к изменению 2 выходных битов. Таким образом, каждый входной бит открытого текста уже через 3 раунда влияет на все выходные биты. Аналогично каждый бит ключа влияет на результат шифрования.

Вторая причина состоит в простоте преобразования. Оно может быть реализовано на любом современном процессоре с минимальными затратами.

При разработке и анализе алгоритма Serpent не было выявлено каких-либо уязвимостей в полной 32-раундовой версии. Но при выборе победителя конкурса AES это было справедливо и для остальных алгоритмов-финалистов.

По мнению создателей Serpent, алгоритм может быть взломан, только если будет создана новая мощная математическая теория.

Стоит отметить, что XSL-атака, если будет доказана эффективность её проведения, ослабит криптостойкость Serpent.

• Ross Anderson, Eli Biham, Lars Knudsen. Serpent: A Proposal for the Advanced Encryption Standard (англ.) (недоступная ссылка). Архивировано 27 февраля 2012 года.
• Ross Anderson, Eli Biham and Lars Knudsen. The Case for Serpent (англ.) (недоступная ссылка) (2000). Архивировано 27 февраля 2012 года.
• Ross Anderson, Eli Biham, Lars Knudsen. Serpent: A Flexible Block Cipher With Maximum Assurance (англ.) (недоступная ссылка). Архивировано 27 февраля 2012 года.
• Nicolas T. Courtois, Josef Pieprzyk. Cryptanalysis of Block Ciphers with Overdefined Systems of Equations (англ.) (недоступная ссылка). Архивировано 27 февраля 2012 года.

• Домашняя страница Serpent
• SCAN’s entry for Serpent
• In Pellicano Case, Lessons in Wiretapping Skills — NYTimes, 5 мая 2008