SHARK
SHARK (англ. Secure Hash Algorithm Regenerative Keys — безопасный хеширующий алгоритм с воссоздающимися ключами) — симметричный алгоритм блочного шифрования, разработанный группой криптографов, среди которых Винсент Рэймен, — автор шифра AES. В теории позволяет использовать блоки и ключи различной длины, однако авторская реализация использует 128-битный ключ и 64-битные блоки. Структура схожа со структурой подстановочно-перестановочной сети.
| SHARK | |
|---|---|
| Создатель | Винсент Рэймен, Йоан Даймен, Барт Пренель, Антун Боссэлерс и Эрик де Вин |
| Создан | 1996 г. |
| Опубликован | 1996 г. |
| Размер ключа | 128 бит |
| Размер блока | 64 бит |
| Число раундов | 6[1](8[2]) |
| Тип | Подстановочно-перестановочная сеть |
История SHARK
Шифр SHARK — первый в серии алгоритмов, разработанных в ходе исследования по созданию безопасных и эффективных алгоритмов блочного шифрования на основе метода Wide Trail design strategy[3]. Результатом исследования позже стало создание стандартного шифра AES[2].
Авторы позиционировали SHARK как алгоритм, призванный заменить широко распространенный в то время шифр DES. К новому алгоритму были предъявлены следующие требования:
- высокая производительность — небольшое число раундов. Для сравнения, в шифре DES использовалось 16 раундов. По словам автором, им удались достичь более чем четырёхкратного ускорения по сравнению с шифрами SAFER и IDEA;
- неуязвимость для линейного и дифференциального криптоанализа, для которых был уязвим DES[1].
Хотя до этого уже существовали шифры на основе SP-сети (MMB, SAFER, 3-Way), SHARK впервые использовал MDS-коды[4] для линейного преобразования, а именно коды Рида-Соломона[1].
Существует два варианта шифра SHARK: SHARK-A (англ. affine transform) и SHARK-E (англ. exor), получившие название благодаря различным способам введения раундовых ключей[5].
Дизайн алгоритма
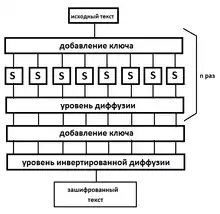
Алгоритм SHARK состоит из трех компонентов:
- нелинейный слой — основан на S-блоках;
- слой диффузии — основан на MDS-кодах[4];
- расписание ключей для получения раундовых ключей из исходного ключа[1].
Каждый компонент алгоритма рассматривается отдельно и каждый должен обладать определёнными свойствами. Так, слой диффузии должен обладать равномерными и хорошими диффузионными свойствами. Нелинейный слой также должен обладать равномерными нелинейными свойствами, причем компоненты алгоритма независимы в следующем смысле: при изменении реализации, например, нелинейного слоя (одни S-блоки заменяются другими S-блоками c такими же характеристиками), защищенность алгоритма остается неизменной. Такая стратегия является вариантом Wide trail strategy[3], описанной в докторской диссертации Йоана Даймена[1].
SHARK состоит из раундов, дополнительного слоя добавления ключа и дополнительно слоя инвертированной диффузии. Каждый раунд, в свою очередь, состоит из добавления ключа, нелинейной замены и слоя диффузии. Дополнительный слой добавления ключа нужен для того, чтобы злоумышленник не смог отделить последний раунд. Дополнительный слой инвертированной диффузии необходим для упрощения операции дешифрования[1].
Слой нелинейный замены состоит из S-блоков, каждый из которых представляет собой -битную перестановку. Таким образом, алгоритм способен шифровать блоки длиной [1].
Слой диффузии
На вход слою диффузии приходят -битных чисел, которые можно рассматривать как элементы над полем . Рассматриваемый слой необходим для создания лавинного эффекта. Этот эффект проявляется в линейном и разностном контекстах:
- Линейный контекст — нет корреляции между линейной комбинации небольшого набора -битных входных данных и линейной комбинации небольшого набора (-битных) выходных данных.
- Разностный контекст — небольшое изменение входных данных влечет значительное изменение данных на выходе, и наоборот, для небольшого изменения выходных данных нужно значительно изменить входные данные[1].
Пусть — обратимое линейное преобразование, — элемент поля , — расстояние Хэмминга, тогда количественно лавинный эффект оценивается числом скачка (англ. branch number) [1].
Если , то . называют оптимальным числом скачка (англ. optimal branch number). В основной статье авторы показали, что с помощью MDS-кодов можно сконструировать обратимое линейное преобразование с оптимальном числом скачка. В реализации используются коды Рида-Соломона[1].
Нелинейный слой (блоки подстановок)
Нелинейные S-блоки обеспечивают защиту от линейного и дифференциального криптоанализов. Одним из важных численных характеристик безопасности шифра служит матрица эксклюзивных ИЛИ (англ. exor table) отображения , элементы которой определяются по формуле , где — обозначает число удовлетворяющих условию элементов, — элементы поля . Большие значения элементов матрицы могут привести к восприимчивости шифра к дифференциальной атаке[1].
Авторами были выбраны S-блоки, основанные на отображении над полем . В этом случае при четном матрица обладает следующими свойствами:
- Дифференциальная 4-стабильность — все элементы матрицы не превосходят 4. В действительности, в каждой строке такой матрицы присутствует ровно один элемент, равный 4, а остальные равны 2 либо 0.
- Минимальное расстояние аффинной функции равно .
- Нелинейный порядок любой линейной комбинации выходных битов равен [1].
Для того чтобы удалить фиксированные точки и , используется обратимое аффинное преобразование выходных бит[1].
Расписание ключей
Расписание ключей (англ. key scheduling) позволяет расширить исходный ключ , получив раундовых ключей . Хорошее планирование позволяет получить раундовые ключи с максимальной энтропией. Авторами предлагаются два способа ввести раундовый ключ:
- Exor — простое исключающее ИЛИ с входными данными в каждом раунде. Соответствующий алгоритм — SHARK-E.
- Affine Transformation — aффинное преобразование входных данных, зависящее от ключа. Соответствующий алгоритм — SHARK-A[1].
Exor
Вычисляется простое исключающее ИЛИ входных бит раунда и подключа. Преимущества метода — быстрота и стабильность: никакой ключ не является сильнее или слабее другого. Недостаток метода — энтропия раундового ключа не превосходит [1].
Affine Transformation
Пусть — невырожденная матрица над полем , зависящая от ключа (точнее, от его расширения). Введем ключевую операцию над входными данными следующим образом: . Это линейная операция, потому она не вводит слабых ключей. Кроме того, энтропия раундовых ключей увеличивается до . Однако, это довольно дорогая в смысле производительности операция, поэтому авторами предлагается ограничить на подпространстве диагональных матриц. В этом случае энтропия раундовых ключей становится близкой к [1].
Генерация подключей
В алгоритме SHARK, генерация раундовых ключей осуществляется следующим образом:
- раундовых -битных ключей инициализируются первыми записями в таблице замещений (англ. substitution table).
- Матрицы инициализируются единичными матрицами.
- Выбранный пользователем ключ конкатенируется сам с собой до тех пор, пока не будет иметь длину бит.
- К полученной в п. 3 последовательности применяется алгоритм SHARK в режиме CFB.
- Первые бит выходных данных используются для формирования раундовых ключей .
- Последние бит выходных данных интерпретируются как элементов поля , и формируют диагональные элементы матриц . Если какой-нибудь элемент равен нулю, то он отбрасываются, а все следующие элементы сдвигаются вниз на единицу. Дополнительные зашифрованные нулевые строки добавляются в конец, чтобы заполнить оставшиеся диагональные элементы[1].
Механизм генерации подключей в принципе позволяет использовать ключ длины бит, но авторы рекомендуют использовать ключ, не превышающий 128 бит[1].
Заметки по реализации
Таблицы замещений
Для того, чтобы добиться высокой производительности, слой диффузии и блоки подстановок объединяются в одну операцию[1]. Пусть обозначают входные данные раунда; — выходные данные; — матрицы перестановок (S-блоки); — матрица, определяющая слой диффузии; и — обозначают сложение и умножение над полем . Тогда
Используя расширенные таблицы замещений размерности , определяемые по формуле , можно записать преобразование в простом виде:
Таким образом, один раунд требует поисков по таблице и бинарных операций. Однако, из-за того что при длине блока бит таблицы занимают байт, алгоритм для блоков длины 128 бит и более оказывался неэффективным для большинства процессоров того времени (1996 год), отсюда происходит существующее ограничение на длину блока в 64 бит ()[2].
Матрица MDS-кода
Для можно построить матрицу, определяющую слой диффузии, на основе кода Рида-Соломона[2].
Дешифрование
Для описания дешифрования рассмотрим 2-х раундовую версию SHARK[1]. Пусть — линейная операция, — нелинейная замена, — операция добавления ключа для раундового ключа . Функция шифрования, в таком случае, равна , где — комбинированная из слоя диффузии и S-блоков операция. Так как операция добавления ключа и операция диффузии — линейные операции, их порядок можно поменять местами[1]:
,
где введено обозначение
Применим полученную формулу к [1]:
Теперь покажем, что операция дешифрования имеет ту же структуру. Для этого сначала обратим операцию шифрования[1]:
Меняя местами операцию добавления ключа и операцию диффузии, получаем ту же структуру, что и в операции шифрования[1]:
Известные атаки
На текущий момент не обнаружено уязвимостей у классической реализации алгоритма. Существуют атаки только на вариации алгоритма:
- В 1997 году Томас Якобсен и Ларс Кнудсен показали, что 64-битная реализация SHARK-E (SHARK с exor стратегией введения раундового ключа) теоретически уязвима для интерполяционной атаки при ограничении на количество раундов до 5, а также 128-битная реализация — при ограничении до 8 раундов. Но они также показали, что для достаточной безопасности необходимо по крайней мере 6 раундов[6].
- В 2013 году Янг Ши (англ. Yang Shi) и Хонгвей Фан (англ. Hongfei Fan) показали, что White-Box реализация[7] SHARK недостаточно безопасна и может быть взломана с фактором работы примерно 1.5 * (2 ^ 47)[8].
Примечания
- Винсент Рэймен, Йоан Даймен, Барт Пренель, Антун Боссэлерс, Эрик де Вин. The Cipher SHARK : PDF.
- Винсент Рэймен, Йоан Даймен. The Design of Rijndael : PDF. — С. 161—165.
- Йоан Даймен. Cipher and Hash Function Design Strategies based on linear and differential cryptanalysis : PDF. Архивировано 16 мая 2018 года.
- MDS-коды — коды с наибольшим кодовым расстоянием
- Scan's entry for Shark.
- Томас Якобсен, Ларс Кнудсен. The Interpolation Attack on Block Ciphers. Springer International Publishing AG (17 мая 2006). Дата обращения: 9 февраля 2018.
- White-box attack context — злоумышленник имеет полный доступ к программной реализации шифра.
- Yang Shi, Hongfei Fan. On Security of a White-Box Implementation of SHARK.
Литература
- Vincent Rijmen, Joan Daemen, Bart Preneel, Antoon Bosselaers, Erik De Win The Cipher SHARK. — The cipher SHARK.
- Joan Daemen, Vincent Rijmen The Design of Rijndael. — The Design of Rijndael.
- Thomas Jakobsen, Lars R. Knudsen The interpolation attack on block ciphers. — The interpolation attack on block ciphers.
- Yang Shi, Hongfei Fan On Security of a White-Box Implementation of SHARK. — On Security of a White-Box Implementation of SHARK.
- Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone. Handbook of Applied Cryptography. — CRC Press, 1996. — С. 281. — 810 с. — ISBN 9781439821916.
