Концентричные объекты

В двумерном пространстве две концентрические окружности обязательно имеют различные радиусы[6]. Однако окружности в трёхмерном пространстве могут быть концентрическими, иметь тот же самый радиус, и, тем не менее, быть различными. Например, два различных меридиана земного глобуса концентричны между собой и самим земным глобусом (если рассматривать Землю как сферу). Более обще, любые два больших круга на сфере концетричны один относительно другого и самой сфере[7].

По теореме Эйлера в геометрии о расстоянии между центром описанной окружности и центром вписанной окружности треугольника две концентрические окружности (с нулевым расстоянием между центрами) являются описанной и вписанной окружностями для треугольника тогда и только тогда, когда радиус одной вдвое больше радиуса другой, и в этом случае треугольник будет правильным.[8].

Описанная и вписанная окружности правильного n-угольника и сам правильный n-угольник концентричны. Для отношения радиусов описанной окружности к радиусу вписанной окружности для различных n — см. Бицентрический многоугольник.

Область плоскости между двумя концентрическими окружностями является кольцом и, аналогично, область пространства между двумя концентрическими сферами является сферической оболочкой[4].

Для заданной точки c на плоскости множество всех окружностей, имеющих точку c в качестве центра, образуют пучок окружностей. Любые две окружности в пучке концентричны и имеют различные радиусы. Любая точка на плоскости, за исключением общего центра, принадлежит ровно одной окружности пучка. Любые две непересекающиеся окружности и любые гиперболические пучки окружностей могут быть преобразованы в множество концентрических окружностей путём преобразования Мёбиуса[9][10].

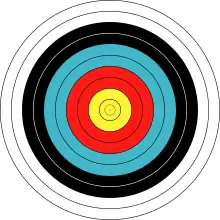
Рябь, образованная падением маленьких объектов в спокойную воду, образует систему концентрических окружностей[11]. Равномерно распределённые окружности на мишени, используемые при стрельбе из лука[12] или подобных спортивных дисциплинах, дают другой известный пример концентрических окружностей.

Коаксиальный кабель — это тип электрического кабеля, в котором комбинация нейтрального слоя и земля окружают полностью центральный проводник(и) в виде концентрических цилиндрических слоёв[13].

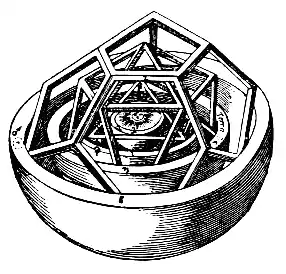
Книга «Тайна мироздания» Иоганна Кеплера представляет космологическую систему в виде концентрических правильных многогранников и сфер[14].

Концентрические окружности также обнаруживаются в диоптрических прицелах (вид механических прицелов), обычно используемых на винтовках. Они обычно представляют собой большой диск с отверстием малого диаметра рядом с глазом стрелка и сферическую мушку (окружность, находящуюся внутри другой окружности, называемой туннелем). Когда элементы прицела правильно выровнены, точка попадания будет в середине фронтального кольца.

• Центрированные многогранные числа
• Гомеоид
• Фокалоид
• Круговая симметрия
• Магические круги

• Geometry: Concentric circles demonstration With interactive animation