Квадрика

Квадрики на евклидовой плоскости соответствуют случаю n = 1, то есть являются кривыми. Обычно их называют не квадриками, а кониками или коническими сечениями.

Квадрики в (трёхмерном действительном) евклидовом пространстве имеют размерность n = 2 и называются поверхностями второго порядка. Проведя ортогональную замену базиса, любую квадрику в евклидовом пространстве можно привести к нормальной форме. В трёхмерном евклидовом пространстве существует 17 таких форм.[2] Из них 5 являются невырожденными (то есть матрица ${\displaystyle {\begin{pmatrix}Q&{\dfrac {P^{T}}{2}}\\{\dfrac {P}{2}}&R\end{pmatrix}}}$ является невырожденной[3]). Вырожденные формы включают в себя плоскости, прямые, точки и даже квадрики без действительных точек.[4]

Невырожденные действительные квадрики в евклидовом пространстве
Эллипсоид	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1}$
Эллиптический параболоид	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0}$
Гиперболический параболоид	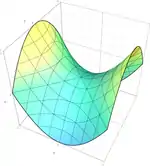${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0}$
Однополостный гиперболоид	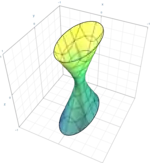${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1}$
Двуполостный гиперболоид	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1}$

Классификация квадрик в трёхмерном аффинном пространстве совпадает с классификацией квадрик в евклидовом пространстве.[5] Различие состоит в том, что любые две квадрики из одного класса можно перевести друг в друга аффинным преобразованием, тогда как соответствующее ортогональное преобразование существует не всегда (например, эллипсоид ${\displaystyle x^{2}+y^{2}+z^{2}=1}$ невозможно перевести движением в эллипсоид ${\displaystyle 2x^{2}+2y^{2}+2z^{2}=1}$).

От квадрики в аффинном пространстве можно перейти к квадрике в проективном пространстве, введя однородные координаты. Пусть в аффинном пространстве введены координаты ${\displaystyle (x_{1},x_{2},\ldots x_{n+1}),}$ тогда в уравнении квадрики достаточно домножить линейные члены на ${\displaystyle x_{0},}$ а свободный член на ${\displaystyle x_{0}^{2}.}$ Уравнение проективной квадрики в однородных координатах имеет вид

${\displaystyle Q(x)=\sum _{ij}a_{ij}x_{i}x_{j}=0.}$

Без ограничения общности можно считать, что матрица ${\displaystyle Q}$ симметрична, то есть ${\displaystyle a_{ij}=a_{ji}.}$ Проективная квадрика называется невырожденной, если соответствующая ей квадратичная форма невырождена.

В действительном проективном пространстве, согласно закону инерции квадратичных форм, любую невырожденную квадратичную форму можно (проективным преобразованием) привести к виду

${\displaystyle Q(x)=\pm x_{0}^{2}\pm x_{1}^{2}\pm \cdots \pm x_{n+1}^{2}}$

Поскольку сигнатура квадратичной формы является её инвариантом, в размерности n = 2 существует ровно три класса эквивалентности:

${\displaystyle Q(x)={\begin{cases}x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\\x_{0}^{2}+x_{1}^{2}+x_{2}^{2}-x_{3}^{2}\\x_{0}^{2}+x_{1}^{2}-x_{2}^{2}-x_{3}^{2}\end{cases}}}$

Эллипсоид, эллиптический параболоид и двуполостный гиперболоид принадлежат второму классу, а гиперболический параболоид и однополостный гиперболоид — третьему (последние две квадрики являются примерами линейчатых поверхностей). Ни одна квадрика в действительном проективном пространстве не принадлежит первому классу, так как соответствующее уравнение определяет пустое множество. В комплексном проективном пространстве все невырожденные квадрики эквивалентны.

• В словарях приводятся различные ударения: квадри́ка[6][7] («русское» произношение) и ква́дрика[8][9] («иностранное» произношение).
• В разговорном языке используется произношение как квадри́ка (Калининградская геометрическая школа), так и ква́дрика[10][11][12]. Не известно примеров другого произношения.

• Математическая энциклопедия. В пяти томах. Том 2, стр.795 (статья «Квадрика»). М.: Советская энциклопедия, 1979—1985.

• Коническое сечение
• Коническая константа
• Кривая второго порядка
• Кубика
• Поверхность второго порядка
• Теорема Брианшона
• Теорема Паскаля
• Фигуры Лиссажу