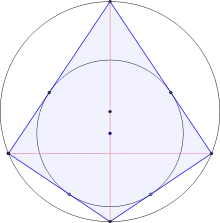
Вписанно-описанный четырёхугольник
Вписанно-описанный четырёхугольник — это выпуклый четырёхугольник, который имеет как вписанную окружность, так и описанную окружность. Из определения следует, что вписанно-описанные четырёхугольники имеют все свойства как описанных четырёхугольников, так и вписанных четырёхугольников. Другие названия этих четырёхугольников: хордо-касающийся четырёхугольник[1] и бицентрический четырёхугольник. Их также называют двух-окружностными четырёхугольниками[2].
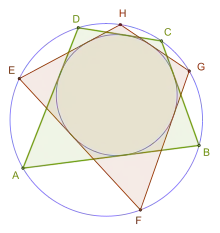
Если две окружности, одна внутри другой, являются вписанной окружностью и описанной окружностью некоторого четырёхугольника, то любая точка на описанной окружности является вершиной какого-то (возможно, другого) вписанно-описанного четырёхугольника, имеющего те же самые вписанные и описанные окружности[3]. Это следствие поризма Понселе, который доказал французский математик Жан-Виктор Понселе (1788–1867).
Специальные случаи
Примерами вписанно-описанных четырёхугольников являются квадраты, прямоугольные дельтоиды и равнобокие описанные трапеции.
Описание

Выпуклый четырёхугольник ABCD со сторонами a, b, c, d является бицентрическим тогда и только тогда, когда противоположные стороны удовлетворяют теореме Пито для описанных четырёхугольников и свойству вписанных четырёхугольников, что противоположные углы в сумме дают 180 градусов, то есть
Три других описания касаются точек, в которых вписанная окружность в описанном четырёхугольнике касается сторон. Если вписанная окружность касается сторон AB, BC, CD и DA в точках W, X, Y и Z соответственно, то описанный четырёхугольник ABCD является также и описанным в том и только в том случае, когда выполняется любое из следующих трёх условий[4]:
- Отрезок WY перпендикулярен XZ
Первое из этих трёх условий означает, что контактный четырёхугольник WXYZ является ортодиагональным четырёхугольником.
Если E, F, G, H являются серединами WX, XY, YZ, ZW соответственно, то описанный четырёхугольник ABCD также является описанным тогда и только тогда, когда четырёхугольник EFGH является прямоугольником[4].
Согласно другому описанию, если I является центром вписанной окружности описанного четырёхугольника, у которого продолжения противоположных сторон пересекаются в точках J и K, то четырёхугольник является описанным тогда и только тогда, когда JIK является прямым углом[4].
Ещё одним необходимым и достаточным условием является то, что описанный четырёхугольник ABCD является описанным тогда и только тогда, когда его прямая Гаусса перпендикулярна прямой Гаусса его контактного четырёхугольника WXYZ. (Прямая Гаусса четырёхугольника определяется средними точками его диагоналей.)[4]
Построение

Имеется простой метод построения бицентрического четырёхугольника:
Построение начинается с вписанной окружности Cr с центром I и радиусом r, затем рисуем две перпендикулярные друг другу хорды WY и XZ во вписанной окружности Cr. На концах хорд проводим касательные a, b, c и d к вписанной окружности. Они пересекаются в точках A, B, C and D, которые являются вершинами вписанно-описанного четырёхугольника[5]. Чтобы нарисовать описанную окружность, рисуем два серединных перпендикуляра p1 и p2 к сторонам вписанно-описанного четырёхугольника a и b соответственно. Они пересекаются в центре O описанной окружности CR на расстоянии x от центра I вписанной окружности Cr.
Справедливость этого построения вытекает из факта, что в описанном четырёхугольнике ABCD контактный четырёхугольник WXYZ имеет перпендикулярные диагонали тогда и только тогда, когда описанный четырёхугольник является также вписанным.
Площадь
Формулы в терминах четырёх величин
Площадь K вписанно-описанного четырёхугольника можно выразить в терминах четырёх величин четырёхугольника несколькими способами. Если a, b, c и d являются сторонами, то площадь задаётся формулой[3][6][7][8][9]
Это частный случай формулы Брахмагупты. Формулу можно получить и прямо из тригонометрической формулы площади описанного четырёхугольника. Заметим, что обратное не выполняется — некоторые четырёхугольники, не являющиеся бицентрическими, также имеют площадь [10]. Примером такого четырёхугольника служит прямоугольник (с разными сторонами, не квадрат).
Площадь может быть выражена в терминах отрезков от вершины до точки касания (для краткости будем называть эти длины касательными длинами) e, f, g, h[11]
Формула площади вписанно-описанного четырёхугольника ABCD с центром вписанной окружности I[7]
Если вписанно-описанный четырёхугольник имеет касательные хорды k, l и диагонали p, q, тогда он имеет площадь[12]
Если k, l являются касательными хордами и m, n являются бимедианами четырёхугольника, тогда площадь может быть вычислена с помощью формулы[7].
Формула не может быть использована, если четырёхугольник является прямоугольным дельтоидом, поскольку в этом случае знаменатель равен нулю.
Если M и N являются серединами диагоналей, а E и F являются точками пересечения продолжения сторон, то площадь вписанно-описанного четырёхугольника задаётся формулой
- ,
где I является центром вписанной окружности[7].
Формулы в терминах трёх величин
Площадь вписанно-описанного четырёхугольника можно выразить в терминах двух противоположных сторон и угла θ между диагоналями согласно формуле[7]
В терминах двух смежных углов и радиуса r вписанной окружности площадь площадь задаётся формулой[7]
Площадь задаётся в терминах радиуса R описанной окружности и радиуса r вписанной окружности как
где θ является любым из углов между диагоналями[13].
Если M и N являются средними точками диагоналей, а E и F являются точками пересечения продолжений противоположных сторон, площадь можно выразить формулой
- ,
где Q является основанием перпендикуляра на прямую EF из центра вписанной окружности[7].
Неравенства
Если r и R являются радиусом вписанной окружности и радиусом описанной окружности соответственно, тогда площадь K удовлетворяет двойному неравенству[14]
Равенство получим, только если четырёхугольник является квадратом.
Другим неравенством для площади будет[15]:p.39,#1203
- ,
где r и R являются радиусом вписанной окружности и радиусом описанной окружности соответственно.
Похожее неравенство, дающее более точную верхнюю границу для площади, чем предыдущее[13]
и равенство достигается тогда и только тогда, когда четырёхугольник является прямоугольным дельтоидом.
Кроме того, со сторонами a, b, c, d и полупериметром s:
- [15]:p.39,#1203
- [15]:p.39,#1203
- [15]:p.39,#1203
Формулы углов
Если a, b, c и d являются длинами сторон AB, BC, CD и DA соответственно во вписанно-описанном четырёхугольнике ABCD, то его углы в вершинах можно вычислить с помощью тангенса[7]:
Если использовать те же обозначения, выполняются следующие формулы для синусов и косинусов[16]:
Угол θ между диагоналями можно вычислить из формулы[8].
Радиус вписанной окружности и радиус описанной окружности
Радиус вписанной окружности r вписанно-описанного четырёхугольника определяется сторонами a, b, c, d по формуле[3]
Радиус описанной окружности R является частным случаем формулы Парамешвары[3]
Радиус вписанной окружности можно выразить также в терминах последовательных касательных длин e, f, g, h согласно формуле[17].
Эти две формулы, фактически, являются необходимыми и достаточными условиями для описанного четырёхугольника с радиусом вписанной окружности r быть вписанным.
Четыре стороны a, b, c, d вписанно-описанного четырёхугольника являются решениями уравнения четвёртой степени
- ,
где s является полупериметром, а r и R являются радиусом вписанной окружности и радиусом описанной окружности соответственно[18].
Если имеется вписанно-описанный четырёхугольник с радиусом вписанной окружности r, касательные длины которых равны e, f, g, h, то существует вписанно-описанный четырёхугольник с радиусом вписанной окружности rv, касательные длины которых равны , где v могут быть любым вещественным числом[19].
Вписанно-описанный четырёхугольник имеет больший радиус вписанной окружности, чем любой другой описанный четырёхугольник, имеющий те же длины сторон в той же последовательности[20].
Неравенства
Радиус описанной окружности R и радиус вписанной окружности r удовлетворяют неравенству
- ,
которое доказал Л. Фейеш Тот в 1948[21]. Неравенство превращается в равенство, только если две окружности концентричны (центры совпадают). В этом случае четырёхугольник является квадратом. Неравенство можно доказать несколькими различными путями, один из путей использует двойное неравенство для площади выше.
Обобщением предыдущего неравенства является[2][22].
- ,
где неравенство превращается в равенство тогда и только тогда, когда четырёхугольник является квадратом[23].
Полупериметр s вписанно-описанного четырёхугольника удовлетворяет[24]
- ,
где r и R являются радиусом вписанной окружности и радиусом описанной окружности соответственно.
Более того,[15]:p.39,#1203
и
- [15]:p.62,#1599
Расстояние между центром вписанной окружности и центром описанной окружностей
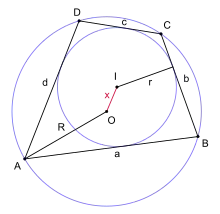
Теорема Фусса
Теорема Фусса даёт связь между радиусом вписанной окружности r, радиусом описанной окружности R и расстоянием x между центром вписанной окружности I и центром описанной окружности O, для любого бицентрического четырёхугольника. Связь задаётся формулой[1][9][25].
Или, эквивалентно,
Формулу вывел Николай Иванович Фусс (1755–1826) в 1792. Решая относительно x, получим
Теорема Фусса для вписанно-описанных четырёхугольников, которая является аналогом теоремы Эйлера для треугольников, утверждает, что если четырёхугольник бицентрический, то его две ассоциированных окружности связаны приведённой выше формулой. Фактически, обратное также выполняется — если даны две окружности (одна внутри другой) с радиусами R и r и расстояние x между их центрами удовлетворяет условию теоремы Фусса, существует выпуклый четырёхугольник, вписанный в одну из окружностей, а другая окружность будет вписана в четырёхугольник[26] (а тогда, по теореме Понселе, существует бесконечно много таких четырёхугольников).
Если использовать факт, что в выражении теоремы Фусса, получим другим способом уже упомянутое неравенство Обобщением неравенства будет[27]
Тождество Карлица
Другая формула расстояния x между центрами вписанной окружности и описанной окружности принадлежит американскому математику Леонарду Карлицу (1907–1999). Формула утверждает, что[28].
- ,
где r и R являются радиусом вписанной окружности и радиусом описанной окружности соответственно, и
- ,
где a, b, c, d являются сторонами вписанно-описанного четырёхугольника.
Неравенства для касательных длин и сторон
Для касательных длин e, f, g, h выполняются следующие неравенства[29]:
и
- ,
где r является радиусом вписанной окружности, R является радиусом описанной окружности, а x является расстоянием между центрами этих окружностей. Стороны a, b, c, d удовлетворяют неравенствам[27]
и
Другие свойства центра вписанной окружности
Центр описанной окружности, центр вписанной окружности и точка пересечения диагоналей во вписанно-описанном четырёхугольнике коллинеарны.[30]
Есть следующее равенство относительно четырёх расстояний между центром вписанной окружности I и вершинами бицентрического четырёхугольника ABCD:[31]
- ,
где r — радиус вписанной окружности.
Если точка P является пересечением диагоналей во вписанно-описанном четырёхугольнике ABCD с центром вписанной окружности I, то[32]
Есть неравенство для радиуса r вписанной окружности и радиуса описанной окружности R во вписанно-описанном четырёхугольнике ABCD[33]
- ,
где I является центром вписанной окружности.
Свойства диагоналей
Длины диагоналей во вписанно-описанном четырёхугольнике можно выразить терминах сторон или касательных длин. Эти формулы верны для вписанных четырёхугольников и описанных четырёхугольников соответственно.
Во вписанно-описанном четырёхугольнике с диагоналями p и q выполняется тождество[34]:
- ,
где r и R являются радиусом вписанной окружности и радиусом описанной окружности соответственно. Это тождество можно переписать как[13]
или, решив его как квадратное уравнение относительно произведения диагоналей, получим
Есть неравенство для произведения диагоналей p, q во вписанно-описанном четырёхугольнике[14]
- ,
где a, b, c, d — стороны. Неравенство доказал Мюррей С. Кламкин в 1967.
См. также
- Вписанно-описанный многоугольник
- Внеописанный четырёхугольник
Примечания
- Dörrie, 1965, с. 188–193.
- Yun, 2008, с. 119—121.
- Eric Weisstein, Bicentric Quadrilateral at MathWorld, , Accessed on 2011-08-13.
- Josefsson, 2010, с. 165–173.
- Alsina, Nelsen, 2011, с. 125–126.
- Josefsson, 2010, с. 129.
- Josefsson, 2011, с. 155–164.
- Durell, Robson, 2003, с. 28, 30.
- Yiu, 1998, с. 158—164.
- Lord, 2012, с. 345—347.
- Josefsson, 2010, с. 128.
- Josefsson, 2010a, с. 129.
- Josefsson, 2012, с. 237–241.
- Alsina, Nelsen, 2009, с. 64–66.
- Inequalities proposed in Crux Mathematicorum, 2007.
- Josefsson, 2012, с. 79–82.
- Radic, Kaliman, Kadum, 2007, с. 41.
- Pop, 2009, с. 754.
- Radic, 2005, с. 9—10.
- Hess, 2014, с. 392–393.
- Radic, 2005.
- Shattuck, 2018, с. 141.
- Josefsson, 2012, с. 81.
- Radic, 2005, с. 13.
- Salazar, 2006, с. 306–307.
- Byerly, 1909, с. 123–128.
- Radic, 2005, с. 5.
- Calin, 2010, с. 153–158.
- Radic, 2005, с. 3.
- Bogomolny, Alex, Collinearity in Bicentric Quadrilaterals , 2004.
- Juan Carlos Salazar, Fuss Theorem for Bicentric Quadrilateral, 2003, .
- Crux Mathematicorum 34 (2008) no 4, p. 242.
- Post at Art of Problem Solving, 2009
- Yiu, 1998, с. 158-164.
Литература
- Heinrich Dörrie. 100 Great Problems of Elementary Mathematics: Their History and Solutions. — New York: Dover, 1965. — С. 188–193. — ISBN 978-0-486-61348-2.
- Eric W. Weisstein. Poncelet Transverse // MathWorld – A Wolfram Web Resource,.
- Martin Josefsson. Characterizations of Bicentric Quadrilaterals // Forum Geometricorum. — 2010. — Т. 10. — С. 165–173.
- Martin Josefsson. Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral // Forum Geometricorum. — 2010a. — Т. 10. — С. 119–130.
- Martin Josefsson. The Area of a Bicentric Quadrilateral // Forum Geometricorum. — 2011. — Т. 11. — С. 155–164.
- Martin Josefsson. A New Proof of Yun’s Inequality for Bicentric Quadrilaterals // Forum Geometricorum. — 2012. — Т. 12. — С. 79–82.
- Claudi Alsina, Roger Nelsen. Icons of Mathematics. An exploration of twenty key images. — Mathematical Association of America, 2011. — С. 125–126. — ISBN 978-0-88385-352-8.
- Nick Lord. Quadrilaterals with area formula // Mathematical Gazette. — 2012. — Июль (т. 96).
- Martin Josefsson. Maximal Area of a Bicentric Quadrilateral // Forum Geometricorum. — 2012. — Т. 12. — С. 237–241.
- Claudi Alsina, Roger Nelsen. When less is more: visualizing basic inequalities. — Mathematical Association of America, 2009. — С. 64–66. — ISBN 978-0-88385-342-9.
- Durell C. V., Robson A. Advanced Trigonometry. — Dover, 2003.
- Radic M., Kaliman Z., Kadum V. A condition that a tangential quadrilateral is also a chordal one. — Mathematical Communications, 2007. — Т. 12. — С. 33–52.
- Ovidiu T. Pop. Identities and inequalities in a quadrilateral // Octogon Mathematical Magazine. — 2009. — Октябрь (т. 17, № 2). — С. 754—763.
- Mirko Radic. Certain inequalities concerning bicentric quadrilaterals, hexagons and octagons // Journal of Inequalities in Pure and Applied Mathematics. — 2005. — Т. 6, вып. 1.
- Zhang Yun. Euler's Inequality Revisited // Mathematical Spectrum. — 2008. — Май (т. 40, № 3). — С. 119—121.
- Mark Shattuck. A Geometric Inequality for Cyclic Quadrilaterals // Forum Geometricorum. — 2018. — Т. 18. — С. 141—154.
- Paul Yiu. Euclidean Geometry. — 1998. — С. 158—164.
- Juan Carlos Salazar. Fuss's Theorem // Mathematical Gazette. — 2006. — Июль (т. 90). — С. 306–307.
- Byerly W. E. The In- and-Circumscribed Quadrilateral // The Annals of Mathematics. — 1909. — Т. 10. — С. 123–128. — doi:10.2307/1967103.
- Ovidiu Calin. Euclidean and Non-Euclidean Geometry a metric approach. — 2nd ed.. — Wiley Custom Publishing, 2010. — С. 153–158.
- Albrecht Hess. On a circle containing the incenters of tangential quadrilaterals // Forum Geometricorum. — 2014. — Т. 14. — С. 389–396.