Прямоугольный дельтоид
Прямоугольный дельтоид — это дельтоид (четырёхугольник, стороны которого можно сгруппировать в две пары смежных сторон одинаковой длины), который может быть вписан в окружность[1]. То есть это дельтоид с описанной окружностью (вписанный дельтоид). Тогда прямоугольный дельтоид является выпуклым четырёхугольником и имеет два противоположных прямых угла[2].
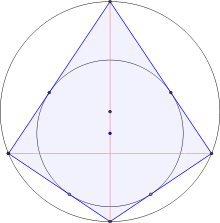
Вписанная окружность
Все прямоугольные дельтоиды являются вписанно-описанными четырёхугольниками (у которых есть описанная и вписанная окружность), поскольку все дельтоиды имеют вписанную окружность. Одна из диагоналей (которая служить осью симметрии) делит прямоугольный дельтоид на два прямоугольных треугольника и является также диаметром описанной окружности.
В описанном четырёхугольнике (то есть обладающем вписанной окружностью), четыре отрезка между центром вписанной окружности и точками касания четырёхугольника разбивают четырёхугольник на четыре прямоугольных дельтоида.
Специальный случай
Специальным случаем прямоугольных дельтоидов являются квадраты, у которых диагонали имеют одинаковую длину и вписанная и описанная окружности концентричны.
Описание
Дельтоид является прямоугольным дельтоидом тогда и только тогда, когда он имеет описанную окружность (по определению). Это эквивалентно тому, что дельтоид имеет два противоположных прямых угла.
Формулы
Поскольку прямоугольный дельтоид можно разбить на два прямоугольных треугольника, следующие формулы легко получаются из хорошо известных свойств прямоугольных треугольников. В прямоугольном дельтоиде ABCD, где два противоположных угла B и D прямые, два других угла могут быть вычислены из
- ,
где a = AB = AD и b = BC = CD. Площадь прямоугольного дельтоида равна
Диагональ AC, которая является осью симметрии, имеет длину
и, поскольку диагонали перпендикулярны (так что прямоугольный дельтоид является ортодиагональным четырёхугольником с площадью ), другая диагональ BD имеет длину
Радиус описанной окружности равен (согласно теореме Пифагора)
и, поскольку все дельтоиды являются описанными, радиус вписанной окружности задаётся формулой
- ,
где s является полупериметром.
Площадь задаётся в терминах радиуса R описанной окружности и радиуса r вписанной окружности как[3].
Если мы обозначим отрезки на диагоналях от точки пересечения до вершин по часовой стрелке через , то
Это прямое следствие теоремы о среднем геометрическом.
Двойственность
Двойственным многоугольником для прямоугольного дельтоида является равнобочная трапеция[1].
Альтернативное определение
Иногда прямоугольный дельтоид определяется как дельтоид с по меньшей мере одним прямым углом[4]. Если имеется только один прямой угол, он должен быть между двумя сторонами равной длины. В этом случае формулы, приведённые выше, не работают.
Примечания
- de Villiers, 2009, с. 154, 206.
- de Villiers, 1994, с. 11–18.
- Josefsson, 2012, с. 237–24.
- 1728 Software Systems, Kite Calculator, accessed 8 October 2012
Литература
- Michael de Villiers. Some Adventures in Euclidean Geometry. — Key Curriculum Press, 2009. — ISBN 978-0-557-10295-2.
- Michael de Villiers. The role and function of a hierarchical classification of quadrilaterals // For the Learning of Mathematics. — 1994. — Т. 14, вып. 1. — .
- Martin Josefsson. Maximal Area of a Bicentric Quadrilateral // Forum Geometricorum. — 2012. — Т. 12. — С. 237–241.