Тензорный скетч
Тензорный скетч (англ. tensor sketch) — метод уменьшения размерности, используемый в статистике, машинном обучении и алгоритмах обработки больших данных[1][2]. Он особенно эффективен применительно к векторам, имеющим тензорную структуру. Такой скетч может быть использован для ускорения билинейного объединения в нейронных сетях и является краеугольным камнем во многих алгоритмах числовой линейной алгебры[3].
История
Термин тензорный скетч (эскиз) был придуман в 2013 г.[4] и в том же году описан как метод Расмусом Пегом[5].
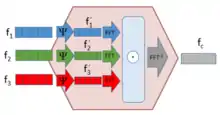
Сначала соответствующий метод базировался на использовании быстрого преобразования Фурье, чтобы реализовать быструю свёртку аналогично отсчётному скетчу. В результате дальнейших исследований его обобщили на значительно больший класс методов уменьшения размерности с помощью случайных тензорных проекций.
Тензорные проекции
В основе одного из вариантов тензорного скетча лежит применение торцевого произведения матриц, предложенного Слюсарем В. И.[6] в 1996 г. (англ. face-splitting product)[7][8][9][10][11].
Торцевое произведение двух матриц с однаковым количеством строк и имеет вид[7][8][9][12]:
Целесообразность использования этого произведения заключается в его свойстве:
где — поэлементное произведение Адамара.
На этой основе произвольный тензорный скетч вида можно представить как , где матрицы и имеют меньшую размерность, и . Поскольку операции и выполнимы за линейное время и соответственно, переход к представлению позволяет выполнить умножение на векторы с тензорной структурой намного быстрее, чем формируется исходное выражение , а именно за время .
Для тензоров более высокого порядка, например, , экономия будет ещё более значимой.
Подобное преобразование удовлетворяет лемме о малых искажениях исходных данных большой размерности.
См. также
Примечания
- Low-rank Tucker decomposition of large tensors using: Tensor Sketch. amath.colorado.edu. Boulder, Colorado: University of Colorado Boulder.
- Ahle, Thomas; Knudsen, Jakob Almost Optimal Tensor Sketch. Researchgate (3 сентября 2019). Дата обращения: 11 июля 2020.
- Woodruff, David P. «Sketching as a Tool for Numerical Linear Algebra.» Theoretical Computer Science 10.1-2 (2014): 1-157.
- (2013) «Fast and scalable polynomial kernels via explicit feature maps» in SIGKDD international conference on Knowledge discovery and data mining., Association for Computing Machinery. DOI:10.1145/2487575.2487591.
- Rasmus, Pagh (2013). “Compressed matrix multiplication”. ACM Transactions on Computation Theory, August 2013 Article No.: 9. Association for Computing Machinery. DOI:10.1145/2493252.2493254.
- Anna Esteve, Eva Boj & Josep Fortiana (2009): Interaction Terms in Distance-Based Regression, Communications in Statistics — Theory and Methods, 38:19, P. 3501
- Slyusar, V. I. (December 27, 1996). “End products in matrices in radar applications” (PDF). Radioelectronics and Communications Systems.– 1998, Vol. 41; Number 3: 50—53.
- Slyusar, V. I. Analytical model of the digital antenna array on a basis of face-splitting matrix products (англ.) // Proc. ICATT- 97, Kyiv : journal. — 1997. — 20 May. — P. 108—109.
- Slyusar, V. I. A Family of Face Products of Matrices and its Properties (англ.) // Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz : journal. — 1999. — Vol. 35, no. 3. — P. 379—384. — doi:10.1007/BF02733426.
- Slyusar, V. I. Generalized face-products of matrices in models of digital antenna arrays with nonidentical channels (англ.) // Radioelectronics and Communications Systems : journal. — 2003. — Vol. 46, no. 10. — P. 9—17.
- Миночкин А.И., Рудаков В.И., Слюсар В.И. Основы военно-технических исследований. Теория и приложения. Том. 2. Синтез средств информационного обеспечения вооружения и военной техники//Под ред. А.П. Ковтуненко. - Киев: «Гранмна». – 2012. C. 7 - 98; 354 - 521 (2012).
- Slyusar, V. I. (1997-09-15). “New operations of matrices product for applications of radars” (PDF). Proc. Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED-97), Lviv.: 73—74.
