Сигмоида

Сигмо́ида — это гладкая монотонная возрастающая нелинейная функция, имеющая форму буквы «S», которая часто применяется для «сглаживания» значений некоторой величины.

Логистическая кривая (сигмоида)

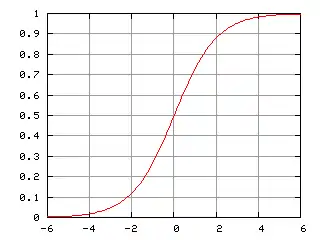
Часто под сигмоидой понимают логистическую функцию

\sigma (x)={\frac {1}{1+e^{-x}}}.

Сигмоида ограничена двумя горизонтальными асимптотами, к которым стремится при стремлении аргумента к $\pm \infty .$ В зависимости от соглашения, этими асимптотами могут быть y = ±1 (в $\pm \infty$ ) либо y = 0 в $-\infty$ и y = +1 в $+\infty$ .

Производная сигмоиды представляет собой колоколообразную кривую с максимумом в нуле, асимптотически стремящуюся к нулю в $+\infty$ .

Семейство функций класса сигмоид

Сравнение некоторых сигмоидных функций, нормализованных таким образом, чтобы производная в начале координат была равна 1

В семейство функций класса сигмоид входят такие функции, как арктангенс, гиперболический тангенс и другие функции подобного вида.

Функция Ферми — Дирака (экспоненциальная сигмоида):

f(x)={\frac {1}{1+e^{-2\alpha x}}},\quad \alpha >0.

Рациональная сигмоида:

f(x)={\frac {x}{|x|+\alpha }},\quad \alpha >0.

Арктангенс:

f(x)=\operatorname {arctg} x.

Гиперболический тангенс:

f(x)=\operatorname {th} {\frac {x}{\alpha }}={\frac {e^{\frac {x}{\alpha }}-e^{-{\frac {x}{\alpha }}}}{e^{\frac {x}{\alpha }}+e^{-{\frac {x}{\alpha }}}}}.

Гладкая ступенька N-го порядка:

f(x)={\begin{cases}\left(\int _{0}^{1}{\big (}1-u^{2}{\big )}^{N}\ du\right)^{-1}\int _{0}^{x}{\big (}1-u^{2}{\big )}^{N}\ du\quad &|x|\leq 1\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\,\quad N\geq 1

Корневая сигмоида:

f(x)={\frac {x}{\sqrt {1+x^{2}}}}.

Логистическая функция:

f(x)=(1+e^{-x})^{-1}.

Обобщённая логистическая функция:

f(x)=(1+e^{-x})^{-\alpha },\quad \alpha >0.

Функция ошибок:

f(x)=\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt.

Функция Гудермана:

f(x)=\operatorname {gd} x=\int _{0}^{x}{\frac {1}{\cosh t}}\,dt=\operatorname {arctg} (\operatorname {sh} x).

Применение

Нейронные сети

Сигмоида применяется в нейронных сетях в качестве функций активации, которая позволяет как усиливать слабые сигналы, так и не насыщаться от сильных сигналов[1].

Производная сигмоиды может быть легко выражена через саму функцию, что позволяет существенно сократить вычислительную сложность метода обратного распространения ошибки, сделав его применимым на практике:

\sigma '(x)=(1+\sigma (x))\cdot (1-\sigma (x))

— для гиперболического тангенса

\sigma '(x)=\sigma (x)\cdot (1-\sigma (x))

— для логистической функции

Логистическая регрессия

Логистическая функция $f(x)={\frac {1}{1+e^{-x}}}$ используется в логистической регрессии следующим образом. В ней решается задача классификации с двумя классами ( $y=0$ и $y=1$ , где $y$ — переменная, указывающая класс объекта), и делается предположение о том, что вероятность принадлежности объекта к одному из классов выражается через значения признаков этого объекта $x_{1},x_{2},...,x_{n}$ (действительные числа):

\mathbb {P} \{y=1\mid x_{1},\ldots ,x_{n}\}=f(a_{1}x_{1}+\ldots +a_{n}x_{n})={\frac {1}{1+\exp(-a_{1}x_{1}-\ldots -a_{n}x_{n})}},

где $a_{1},...,a_{n}$ — некоторые коэффициенты, требующие подбора, обычно, методом наибольшего правдоподобия.

Выбор именно этой функции $f(x)$ можно обосновать, рассматривая логистическую регрессию, как обобщённую линейную модель в предположении, что зависимая переменная $y$ распределена по закону Бернулли.

См. также

Искусственная нейронная сеть
Перцептрон
Модифицированный гиперболический тангенс

Литература

Mitchell, Tom M. Machine Learning. — WCB–McGraw–Hill, 1997. — ISBN 0-07-042807-7.

Примечания

Функции активации в нейронных сетях

Ссылки

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Функции активации в нейронных сетях

Машинное обучение и data mining
Задачи	Задача классификации Обучение без учителя Обучение с частичным привлечением учителя Регрессионный анализ AutoML Ассоциативные правила Выделение признаков Обучение признакам Обучение ранжированию Грамматический вывод Онлайновое обучение
Обучение с учителем	Метод k-ближайших соседей Наивный байесовский классификатор Дерево решений Метод опорных векторов Линейная регрессия Логистическая регрессия Перцептрон Ансамбли моделей Бэггинг Бустинг Random forest Метод релевантных векторов
Кластерный анализ	Метод k-средних Метод нечёткой кластеризации Иерархическая кластеризация EM-алгоритм BIRCH CURE DBSCAN OPTICS Mean-shift
Снижение размерности	Факторный анализ Метод главных компонент CCA ICA LDA Неотрицательное матричное разложение t-SNE
Структурное прогнозирование	Графовая вероятностная модель Байесовская сеть Скрытая марковская модель CRF
Выявление аномалий	Метод k-ближайших соседей Локальный уровень выброса
Графовые вероятностные модели	Байесовская сеть Марковская сеть Скрытая марковская модель
Нейронные сети	Ограниченная машина Больцмана Самоорганизующаяся карта Функция активации Сигмоида Softmax Радиально-базисная функция Метод обратного распространения ошибки Глубокое обучение Многослойный перцептрон Рекуррентная нейронная сеть Долгая краткосрочная память Управляемый рекуррентный блок Свёрточная нейронная сеть U-Net Автокодировщик
Обучение с подкреплением	Марковский процесс Уравнение Беллмана Жадный алгоритм Q-обучение SARSA Temporal difference (TD)
Теория	Теория Вапника — Червоненкиса Дилемма смещения–дисперсии Теория вычислительного обучения Минимизация эмпирического риска Оккамово обучение PAC learning Статистическая теория обучения
Журналы и конференции	NeurIPS ICML ML JMLR ArXiv:cs.LG