Описанное и вписанное конические сечения
Описанное коническое сечение или описанная коника для треугольника — это коническое сечение, проходящее через три вершины треугольника[1], а вписанное коническое сечение или вписанная коника — это вписанное в треугольник коническое сечение, т.е. касающееся сторон треугольника (возможно, не самих сторон, а их продолжений) [2]

Пусть даны три различные точки A,B,C, не лежащие на одной прямой, и пусть ΔABC — треугольник, имеющий эти точки в качестве вершин. Обычно считается, что буква, например A, обозначает не только вершину A, но и прилежащий к ней угол BAC. Пусть a = |BC|, b = |CA|, c = |AB| являются длинами сторон треугольника ΔABC.
В трилинейных координатах описанное коническое сечение — это геометрическое место точек X = x : y : z, удовлетворяющих уравнению
- uyz + vzx + wxy = 0,
для некоторой точки u : v : w. Изогональное сопряжение любой точки из X на сечении, отличной от A,B,C, является точкой на прямой
- ux + vy + wz = 0.
Эта прямая имеет с описанной вокруг треугольника ΔABC окружностью 0,1 или 2 общие точки в зависимости от того, является коническое сечение эллипсом, параболой или гиперболой.
Вписанное коническое сечение касается трёх прямых, проходящих через вершины треугольника ΔABC (продолжения сторон) и задаётся уравнением
- u2x2 + v2y2 + w2z2 − 2vwyz − 2wuzx − 2uvxy = 0.
Центры и касательные прямые
Описанная коника
Центр описанного конического сечения — это точка
- u(−au + bv + cw) : v(au − bv + cw) : w(au + bv − cw).
Прямые, касательные коническому сечению в точках A,B и C, задаются уравнениями
- wv + vz = 0,
- uz + wx = 0,
- vx + uy = 0.
Вписанная коника
Центр вписанного конического сечения — это точка
- cy + bz : az + cx : bx + ay.
Касательные к этой конике — это стороны треугольника ΔABC, и они задаются уравнениями x = 0, y = 0, z = 0.
Другие свойства
Описанные конические сечения
- Любое описанное коническое сечение, не являющееся окружностью, пересекает описанную вокруг ΔABC окружность в точке, отличной от A, B и C, которую часто называют четвёртой точкой пересечения, и она имеет трилинейные координаты
- (cx − az)(ay − bx) : (ay − bx)(bz − cy) : (bz − cy)(cx − az)
- Если точка P = p : q : r лежит на описанном коническом сечении, то прямая, касательная сечению в точке P, задаётся уравнением
- (vr + wq)x + (wp + ur)y + (uq + vp)z = 0.
- Описанное коническое сечение является параболой тогда и только тогда, когда
- u2a2 + v2b2 + w2c2 − 2vwbc − 2wuca − 2uvab = 0,
- и гиперболой тогда и только тогда, когда
- u cos A + v cos B + w cos C = 0.
- Из всех треугольников, вписанных в заданный эллипс, центроид треугольника с наибольшей площадью совпадает с центром эллипса[3]. Эллипс, проходящий через три вершины треугольника, с центром, совпадающим с центроидом треугольника, называется описанным эллипсом Штейнера.
Вписанные конические сечения
- Вписанное коническое сечение является параболой тогда и только тогда, когда
- ubc + vca + wab = 0,
- и в этом случае коническое сечение касается одной стороны треугольника извне и касается продолжения двух других сторон.
- Предположим, что p1 : q1 : r1 и p2 : q2 : r2 различные точки, и пусть
- X = (p1 + p2t) : (q1 + q2t) : (r1 + r2t).
- Когда параметр t пробегает все вещественные числа, геометрическое место точек X является прямой. Определим
- X2 = (p1 + p2t)2 : (q1 + q2t)2 : (r1 + r2t)2.
- Геометрическое место точек X2 является вписанным коническим сечением, обязательно эллипсом, которое задаётся уравнением
- L4x2 + M4y2 + N4z2 − 2M2N2yz − 2N2L2zx − 2L2M2xy = 0,
- где
- L = q1r2 − r1q2,
- M = r1p2 − p1r2,
- N = p1q2 − q1p2.
- Точка внутри треугольника является центром вписанного в треугольник эллипса тогда и только тогда, когда точка лежит внутри треугольника, вершинами которого служат середины исходного треугольника[4]. Для точки внутри серединного треугольника эллипс с центром в этой точке единственен[5].
- Вписанный эллипс с наибольшей площадью является вписанным эллипсом Штейнера, который называется также серединным вписанным эллипсом. Центр этого эллипса совпадает с центроидом треугольника[6]. В общем случае отношение площади вписанного эллипса к площади треугольника в терминах барицентрических координат центра эллипса равно[7].
- и это отношение максимизируется при совпадении с барицентрическими координатами центроида треугольника
- Прямые, соединяющие точки касания любого вписанного в треугольник эллипса с противолежащей вершиной, пересекаются в одной точке[8].
Расширение на четырёхугольники
Все центры вписанных в четырёхугольник эллипсов лежат на отрезке, соединяющем середины диагоналей четырёхугольника[9].
Примеры
- Описанное коническое сечение
 Вписанный и описанный эллипсы Штейнера
Вписанный и описанный эллипсы Штейнера- Описанная окружность, единственная окружность, проходящая через три вершины треугольника
- Описанный эллипс Штейнера, единственный эллипс, проходящий через все три вершины треугольника, с центром, совпадающим с центроидом треугольника
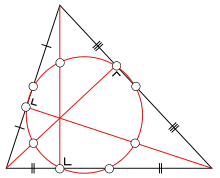 9 точек
9 точек - Гипербола Киперта, единственная коника, которая проходит через три вершины треугольника, его центроид и его ортоцентр
- Гипербола Ержабека, гипербола с центром, совпадающим с центром окружности девяти точек, проходящей через три вершины треугольника, центр его описанной окружности, ортоцентр и другие замечательные центры
- Гипербола Фейербаха, проходящая через ортоцентр треугольника, точку Нагеля и другие замечательные точки, имеет центр на окружности девяти точек.
- Вписанное коническое сечение
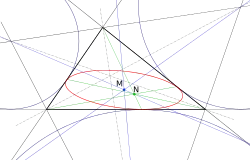 Эллипс Мандара (красный)
Эллипс Мандара (красный)- Вписанная окружность, единственная окружность, касающаяся изнутри стороны треугольника
- Вписанный эллипс Штейнера, единственный эллипс, касающийся трёх сторон треугольника в серединах сторон
- Эллипс Мандара, единственный эллипс, касающийся сторон треугольника в точках касания внешнеописанных окружностей
- Парабола Киперта
- Парабола Иффа
Примечания
- Weisstein, Eric W. "Circumconic." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Circumconic.html
- Weisstein, Eric W. "Inconic." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Inconic.htm (недоступная+ссылка)
- Chakerian, 1979, с. 147.
- Chakerian, 1979, с. 139.
- Chakerian, 1979, с. 142.
- Chakerian, 1979, с. 145.
- Chakerian, 1979, с. 143.
- Chakerian, 1979, с. 148.
- Chakerian, 1979, с. 136.
Литература
G. D. Chakerian. A Distorted View of Geometry // Mathematical Association of America / R. Honsberger. — Washington, DC, 1979.
Ссылки
- Circumconic at MathWorld
- Inconic at MathWorld