Троичные функции
Троичной функцией в теории функциональных систем и троичной логике называют функцию типа , где — троичное множество, а — неотрицательное целое число, которое называют арностью или местностью функции.
Элементы множества — цифровые знаки 0, 1 и 2 могут интерпретироваться как логические «ложь», «неизвестно» и «истина», в общем случае их смысл может быть любым. Элементы называют троичными векторами. В случае n = 0 троичная функция превращается в троичную константу.
Каждая троичная функция арности n полностью определяется заданием своих значений на своей области определения, то есть на всех троичных векторах длины n. Число таких векторов равно 3n. Поскольку на каждом векторе трёхзначная функция может принимать одно из трёх различных значений, то количество всех n-арных троичных функций равно 3(3n) (скобки нужны, так как запись 33n не обладает свойством ассоциативности и 3(32)=39=19683, а (33)2=272=729).
Например, существует 3(30) = 3 нульарных троичных логических функций — константы 0, 1 и 2; 3(31) = 27 унарных троичных логических функций, 3(32) = 19683 бинарных троичных логических функций и т. д.
Троичные логические функции (классификация)
Уровни привязки значений к трём состояниям троичных устройств
В некоторых троичных устройствах все три состояния одинаковы и ни логические ни арифметические значения не определены[1], не определено и направление сдвига, либо правое (по часовой стрелке), либо левое (против часовой стрелки), но на этом уровне уже можно закрепить одно из двух направлений вращения и уже отличать левое вращение от правого вращения.
На втором уровне за тремя состояниями могут быть закреплены три значения, но ещё без привязки арифметических значений, например, треугольник, квадрат и круг. На втором уровне становится возможным привязка логических значений («ложно», «не определено», «истинно»), например:
«треугольник» = «ложно»,
«квадрат» = «не определено»,
«круг» = «истинно»,
хотя в общем случае привязка может быть и другой.
На втором уровне логические значения арифметических значений не имеют.
На третьем уровне трём состояниям приписываются арифметические значения: 0, 1 и 2 или −1, 0 и +1. На третьем уровне логические значения условно имеют и арифметические значения. Наиболее часто встречается привязка арифметических значений не совместимая с обычной привязкой в двоичной логике:
«ложно» = −1,
«не определено» = 0,
«истинно» = +1,
хотя в общем случае привязка арифметических значений может быть и другой, например, привязка:
«ложно» = 0,
«не определено» = 2,
«истинно» = 1,
совместима с обычной привязкой в двоичной логике и соответствует левому вращению при обычной привязке последовательности арифметических значений (0,1,2).
В других троичных устройствах три состояния отличаются, например, по полярности напряжения, и не равнозначны[2]. В этих устройствах очень сильна привязка к уровням напряжения и арифметических и логических значений:
«отрицательное напряжение» = «-1» = «-» = «ложно»,
«близкое к нулю напряжение» = «0» = «не определено»,
«положительное напряжение» = «+1» = «+» = «истинно»,
но и в этих устройствах возможны другие привязки.
Для работы с третьим логическим значением — «не определено» лучше подходят четверичная логика, восьмиричная логика и другие логики кратные 4, чем троичная логика.
Обозначения троичных функций
В общем случае, как в патентном деле, обозначение может быть любым, но необходимо указывать что обозначает каждый элемент в обозначении.
Единой системы обозначений троичных функций ещё не сложилось. Разные авторы применяют разные системы обозначений троичных функций. Пример различных обозначений унарных троичных функций разными авторами приведён в таблице 3 и в подразделе «Обозначения» там же.
При одновременной работе с троичными и двоичными функциями необходимо указывать троичность или двоичность. Это можно сделать буквами T (Ternary) и B (Binary). Например, FT — троичная функция, а FB — двоичная функция.
Так как функции могут иметь разное количество аргументов (арность), то необходимо указывать и арность функций. Так как унарные, бинарные, тринарные и т. д. функции имеются и в двоичной и в троичной и в более -ичных системах, то обозначение системы должно предшествовать обозначению арности. Например, FT1 — троичная унарная функция, FT2 — троичная бинарная функция, FT3 — троичная тринарная функция.
Так как половина номеров разных троичных симметричных и троичных несимметричных функций совпадают, то нужно указывать симмеричность или несимметричность номера функции. Это можно сделать буквами S (Symmetric) и N (Nonsymmetric). Например, FT1S — троичная унарная функция с симметричным номером, FT1N — троичная унарная функция с несимметричным номером, а FT2B1N — смешанная функция с двумя троичными аргументами, с одним двоичным аргументом и с несимметричным номером.
После можно поставить номер функции. Например, FT1N7 — троичная унарная функция с несимметричным номером «7».
Так как некоторые разные номера в троичном и в десятичном виде совпадают, например, 22 троичное равно 8 десятичным, то после номера нужно ставить индекс обозначающий основание системы счисления. Например, FB2N2210, FT2S223, FT2N2210 — это три разные функции.
Названия троичных функций
Как и в двоичной логике, троичная функция может не иметь собственного названия словами, тогда её называют по номерному обозначению, или одна и та же функция может иметь одно или несколько собственных названий словами, в зависимости от области применения.
Соответствия троичной несимметричной и троичной симметричной систем обозначений
В троичной симметричной системе обозначений арифметические значения −1, 0 и +1 очень сильно связаны с логическими обозначениями (−1, 0, +1) или (−, 0, +). Во втором обозначении 1 явно не присутствует, но неявно подразумевается.
В троичной несимметричной системе обозначений, кроме 0 и +1, арифметические значения −1, 0 и +1 менее сильно связаны с логическими обозначениями (0,1,2).
Из таблицы 4 следует, что:
- F1TN0 = F1TS-13
- …
- F1TN13 = F1TS0
- …
- F1TN26 = F1TS+13
или
- F1TS-13 = F1TN0
- …
- F1TS0 = F1TN13
- …
- F1TS+13 = F1TN26,
то есть трёхразрядные троичные номера унарных троичных функций с симметричным кодированием сдвинуты по отношению к номерам унарных троичных функций с несимметричным кодированием на
Девятиразрядные троичные номера бинарных троичных функций с симметричным кодированием сдвинуты по отношению к номерам бинарных троичных функций с несимметричным кодированием на
Троичное несимметричное кодирование удобнее в общетроичных применениях. Троичное симметричное кодирование удобнее при работе с троичными симметричными числами. Не зависимо от системы кодирования, сами функции выполняют с операндами (аргументами) одно и то же действие, даже с не упомянутыми выше системами кодирования.
Перевод троичных несимметричных чисел в троичные симметричные числа
Троичные несимметричные числа с кодировкой (-1,0,+1)=(0,1,2) относительно просто преобразуются в троичные симметричные числа с кодировкой (-1,0,+1)=(2,0,1) с помощью следующего алгоритма[3] (Ошибка Депмана И. Я.: Для записи цифр в трёхзначных системах, в том числе и в числовых троичных системах, требуется три знака. В обозначениях Депмана третьим знаком является надчёркнутая единица — «1», но третьим знаком может быть и «2» и «i» и «7» и «N» и «n» и любой другой знак отличный от знаков «0» и «1».):
1. Начиная со младшего разряда троичного несимметричного числа с кодировкой (-1,0,+1)=(0,1,2):
2. Если число в текущем разряде больше 1 (2 или 3), то в следующий разряд прибавляется 1 (2 остаётся, но уже как обозначение −1);
если число в текущем разряде равно 3, то текущий разряд устанавливается в 0.
3. Переход к следующему по старшинству разряду.
Для отрицательных троичных несимметричных чисел преобразование делают от модуля троичного несимметричного числа, а в результате, во всех разрядах, заменяют «1» на «2», а «2» на «1» с помощью троичной симметричной функции Swap12(X).
Нульарные троичные логические операции (функции) с унарным выходом
Всего существуют простейшие нульарные троичные функции (троичные константы).
С кодированием в троичной несимметричной системе счисления:
| Обозначение | Название | Значение |
|---|---|---|
| FT0N0 | Логический тождественный ноль | 0 |
| FT0N1 | Логическая тождественная единица | 1 |
| FT0N2 | Логическая тождественная двойка | 2 |
С кодированием в троичной симметричной системе счисления:
| Обозначение | Название | Значение |
|---|---|---|
| FT0S-1 | Тождественная минус единица | -1 |
| FT0S0 | Тождественный ноль | 0 |
| FT0S1 | Тождественная плюс единица | 1 |
Унарные троичные логические функции
Унарные троичные логические функции с унарным выходом
Всего существует простейших унарных (с одним входом, с одним аргументом, с одним операндом, одноместных) троичных функций, где m — число выходов, выходная арность функции. Для унарных (с одним входом) троичных функций с унарным выходом m=1 и их число равно .
Количество простейших унарных троичных функций равно числу размещений с повторениями (выборок с возвращением) при k=n=3:
Так как возможны более сложные функции, дающие при подаче на вход одного трита тот же результат, что и простейшие унарные троичные функции, то число более сложных троичных функций с нижеприведёнными результатами от одного трита теоретически бесконечно.
Таблица 1. Результаты действия простейших унарных троичных функций при последовательной подаче на вход трёх значений троичного разряда (трита): 0, 1 и 2.
В несимметричной троичной системе кодирования (-1,0,+1) = (0,1,2):
Таблица 3.
| y\x | 2 | 1 | 0 | название | обозначение |
|---|---|---|---|---|---|
| FT1N0=FT1S-13 | 0 | 0 | 0 | тождественный минимум, тождественный ноль, переход в 0 | F000(X) = 0 |
| FT1N1=FT1S-12 | 0 | 0 | 1 | троичная эмуляция двоичной функции NOT2, переходник в двоичную | F001(X) = NOT2(X) |
| FT1N2=FT1S-11 | 0 | 0 | 2 | переходник в двоичную | F002(X) |
| FT1N3=FT1S-10 | 0 | 1 | 0 | троичная эмуляция двоичной функции YES2, переходник в двоичную | F010(X) = YES2(X) |
| FT1N4=FT1S-9 | 0 | 1 | 1 | троичная эмуляция двоичной функции «тождественная 1», переходник в двоичную | F011(X) = 12 |
| FT1N5=FT1S-8 | 0 | 1 | 2 | обмен 0 и 2, обмен двух младших значений при кодировании (-1,0,+1)=(2,0,1), обмен двух крайних значений («инверсия Лукасевича») при кодировании (-1,0,+1)=(0,1,2) | F1TN510(X) = F0123(X) = Swap02(X) |
| FT1N6=FT1S-7 | 0 | 2 | 0 | переходник в двоичную | F020(X) |
| FT1N7=FT1S-6 | 0 | 2 | 1 | вращение вправо (вперёд, вверх) на 1 шаг (+1 шаг, +1/3 оборота, +120°), циклический сдвиг вправо (вперёд, вверх) на 1 шаг (+1 шаг, +1/3 оборота, +120°), Rotate Up по Стиву Граббу[4], Cicle Up[5] | F021(X) = RotF(x) = RotU(x) = RotR(x) = CicleShiftU(x) |
| FT1N8=FT1S-5 | 0 | 2 | 2 | переходник в двоичную | FT1N810(X) = F0223(X) |
| FT1N9=FT1S-4 | 1 | 0 | 0 | не циклический сдвиг влево (назад, вниз) с пределом 0, не циклический сдвиг влево (назад, вниз) на −1 с пределом 0, не циклический Decrement с пределом 0, Shift Down по Стиву Граббу[6] | F100(X) = ShiftD(x) = ShiftL(X) |
| FT1N10=FT1S-3 | 1 | 0 | 1 | переходник в двоичную | F101(X) |
| FT1N11=FT1S-2 | 1 | 0 | 2 | вращение влево (назад, вниз) на 1 шаг (-1 шаг, −1/3 оборота, −120°), циклический сдвиг влево (назад, вниз) на 1 шаг (-1 шаг, −1/3 оборота, −120°), Rotate Down по Стиву Граббу[7], Cicle Down[5] | F102(X) = RotB(x) = RotD(x) = RotL(x) = CicleShiftD(x) |
| FT1N12=FT1S-1 | 1 | 1 | 0 | переходник в двоичную | F110(X) |
| FT1N13=FT1S0 | 1 | 1 | 1 | тождественная середина, переход в 1, тождественная единица | F111(X) = 1 |
| FT1N14=FT1S+1 | 1 | 1 | 2 | переходник в двоичную | FT1N1410(X) = F1123(X) |
| FT1N15=FT1S+2 | 1 | 2 | 0 | обмен 1 и 2, обмен двух крайних значений («инверсия Лукасевича») при кодировании (-1,0,+1)=(2,0,1), обмен двух старших значений при кодировании (-1,0,+1)=(0,1,2) | FT1N1510(X) = F1203(X) = Swap12(X) |
| FT1N16=FT1S+3 | 1 | 2 | 1 | переходник в двоичную | F121(X) |
| FT1N17=FT1S+4 | 1 | 2 | 2 | переходник в двоичную | FT1N1710(X) = F1223(X) |
| FT1N18=FT1S+5 | 2 | 0 | 0 | переходник в двоичную | F200(X) |
| FT1N19=FT1S+6 | 2 | 0 | 1 | обмен 0 и 1, обмен двух старших значений при кодировании (-1,0,+1)=(2,0,1), обмен двух младших значений при кодировании (-1,0,+1)=(0,1,2) | FT1N1910(X) = F2013(X) = Swap01(X) |
| FT1N20=FT1S+7 | 2 | 0 | 2 | переходник в двоичную | F202(X) |
| FT1N21=FT1S+8 | 2 | 1 | 0 | вращение нулевое, повторитель, Yes, Buffer1, Delay1 (линия задержки на 1 типовую задержку), тождественная функция | F210(X) = Yes(x) = Rot0(x) = CicleShift0(X) = x |
| FT1N22=FT1S+9 | 2 | 1 | 1 | переходник в двоичную | F211(X) |
| FT1N23=FT1S+10 | 2 | 1 | 2 | переходник в двоичную | F212(X) |
| FT1N24=FT1S+11 | 2 | 2 | 0 | переходник в двоичную | F220(X) |
| FT1N25=FT1S+12 | 2 | 2 | 1 | не циклический сдвиг вправо (вперёд, вверх) с пределом 2, не циклический сдвиг вправо (вперёд, вверх) на +1 с пределом 2, не циклический Increment с пределом 2, Shift Up по Стиву Граббу[8] | F221(X) = ShiftU(x) |
| FT1N26=FT1S+13 | 2 | 2 | 2 | тождественный максимум, переход в 2, тождественная двойка | F222(X) = 2 |
По таблице видно, что при последовательной подаче на вход функции значений от 0 до 2, на выходе функции образуется строка, например, «022»3, которая является и номером функции и строкой её действия, то есть и номер функции и строка её действия содержатся в самой функции. Это свойство может оказаться полезным в случае невозможности чтения номера функции на корпусе микросхемы (стёрся, закрашен, не доступен).
По таблице видно, что выходные триты, после действия функций, в 21 случае из 27 теряют трёхзначность и в 18 случаях становятся двухзначными (переходниками в двоичную логику), а в 3 случаях становятся однозначными константами (переходниками к константам) (FT1N0, FT1N13 и FT1N26), и только в 6 случаях (три обмена, два вращения и повторитель) остаются трёхзначными (FT1N5, FT1N7, FT1N11, FT1N15, FT1N19 и FT1N21).
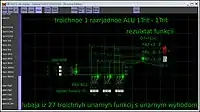
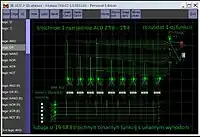
Все 27 унарных троичных операций (функций) выполняются троичным унарным с унарным выходом АЛУ (1Трит-1Трит) в трёхбитной одноединичной системе троичных логических элементов, снимок модели которого в логическом симуляторе Atanua приведён на рисунке справа, и записываются в троичный триггер с соответствующей логикой управления.
Обозначения
Для обозначения унарных троичных функций достаточно любых трёх троичных знаков (33=27), 4/3 девятеричного знака (9(4/3)=27) или одного двадцатисемеричного знака, следовательно, так как возможно бесконечное количество таких знаков, возможно бесконечное множество обозначений унарных троичных функций. Из этого множества обозначений числовые обозначения по результатам действия функций являются естественными обозначениями.
Цифровые обозначения могут быть постфиксными надстрочными, строчными и подстрочными и префиксными надстрочными, строчными и подстрочными, при этом для надстрочных и подстрочных обозначений нужно набирать пять знаков для открывающих и шесть знаков для закрывающих скобок, поэтому проще цифровые строчные обозначения с обычными скобками.
Grabb[10] использует для обозначения шесть знаков: ∪, ∩, ↘, ↗, A, A, из которых 5 труднонабираемы на клавиатуре. Два шестеричных знака могут выразить до 62=36 функций, тем не менее Grabb использует для обозначения −7, −3, 3 и 7 функций четыре знака, что относительно избыточно (64=1296).
Mouftah использует для обозначения 16 знаков: ¬, ¬, ⌐, ⌐, ┘, ┘, └, └, ⊼, ⊽, 0, +, (,), A, A, из которых 11 трудно набираемы на клавиатуре. Два шестнадцатеричных знака могут выразить до 112=256 функций, тем не менее для −6 и −2 функций Mouftah использует 11 знаков, что относительно избыточно (1611=17592186044416).
Yoeli обозначает положительные декодеры −1, 0 и +1 с двумя и тремя трудно набираемыми на клавиатуре надстрочными индексами, при этом не описываются положительные декодеры с двумя 0, нулевые декодеры с двумя 1 и с двумя −1, отрицательные декодеры с двумя 0 и с двумя 1.
В симметричной троичной системе:
Таблица 4.
| y\x | 1 | 0 | i | название | обозначение | F#[5] | Grubb | Mouftah | Название по Mouftah/Yoeli | [5] | Diff:101 | Маслов С. П.[11] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FT1S-13=FT1N0 | i | i | i | переходник в −1, тождественная −1, тождественный минимум | Fiii(X) = −1 | 111 | always output 1 | |||||
| FT1S-12=FT1N1 | i | i | 0 | сдвиг вниз, сдвиг на −1 | Fii0(X) | ii0 | ↘A = Shift Down | ¬┘A | -L, M3 | |||
| FT1S-11=FT1N2 | i | i | 1 | переходник в двоичную, детектор −1 с true=1 false=-1 | Fii1(X) | ii1 | ∩↗A | └┘A = ┘A = ┘A = ┘┘A | x1 (Yoeli), decode-1 | |||
| FT1S-10=FT1N3 | i | 0 | i | переходник в двоичную, замена 1 на −1 | Fi0i(X) | i0i | ↘∩A | |||||
| FT1S-9=FT1N4 | i | 0 | 0 | переходник в двоичную | Fi00(X) | i00 | ↘↗A | ⌐A | Reverse Diode | M8 | ||
| FT1S-8=FT1N5 | i | 0 | 1 | обмен +1 и −1, «инверсия Лукасевича», «Invert» по Стиву Граббу[12], Complement(F210) по Полю Фальстаду[13] | Fi01(X) = «NOTL(Х)» = «NotL(X)» = «InvL(X)» = «Not0(X)» = Swap+1/-1 | 101 | swap1/1, A | A | Simple Ternary Inverter | \'/ | ||
| FT1S-7=FT1N6 | i | 1 | i | переходник в двоичную, детектор 0 с true=1 false=-1 | Fi1i(X) | i1i | ∩↗∪A | ┘(A + A) | x0 (Yoeli), decode-0 | |||
| FT1S-6=FT1N7 | i | 1 | 0 | вращение вперёд на 1/3 оборота (+120°) | Fi10(X) = RotF(X) = RotU(X) = RotRight(x) | 011 | rotate up, ∩A | (└A ⊼ 0)⊼(┘A) — inverse cycling gate | cycle up | /// | ||
| FT1S-5=FT1N8 | i | 1 | 1 | переходник в двоичную, F220 по Полю Фальстаду[14], «инверсия Лукасевича» от детектора +1 | Fi11(X) | i11 | ∪↘A | ┘└A = ┘A = └└A | ||||
| FT1S-4=FT1N9 | 0 | i | i | не циклический сдвиг вниз, не циклический сдвиг на −1 | F0ii(X) | 0ii | ↘A | ⌐└A | Earthed Negative Ternary Inverter | M7 | ||
| FT1S-3=FT1N10 | 0 | i | 0 | переходник в двоичную | F0i0(X) | 0i0 | ∪↗∪A | |||||
| FT1S-2=FT1N11 | 0 | i | 1 | вращение назад на 1/3 оборота (−120°) | F0i1(X) = RotB(x) = RotD(X) = RotLeft(x) | 110 | rotate down, ∪A | (┘A ⊽ 0)⊽(└A) — cycling gate | cycle down | \\\ | ||
| FT1S-1=FT1N12 | 0 | 0 | i | переходник в двоичную, замена +1 на 0 | F00i(X) | 00i | ∪↗A | ⌐└A = ⌐A | -R, M4 | |||
| FT1S0=FT1N13 | 0 | 0 | 0 | переходник в 0, тождественный 0, тождественная середина | F000(X) = 0 | 000 | always output 0 | |||||
| FT1S+1=FT1N14 | 0 | 0 | 1 | F211 по Полю Фальстаду[15], переходник в двоичную | F001(X) | 001 | ↗↘A | ¬A | Forward Diode | M5 | ||
| FT1S+2=FT1N15 | 0 | 1 | i | обмен 0 и 1 | F01i(X) = «NOT0(Х)» = «NOT-1(X)» | 110 | swap 0/1 | swap 0/1 | '/\ | |||
| FT1S+3=FT1N16 | 0 | 1 | 0 | переходник в двоичную | F010(X) | 010 | ∩↘∩A | |||||
| FT1S+4=FT1N17 | 0 | 1 | 1 | F221 по Полю Фальстаду[16], переходник в двоичную | F011(X) | 011 | ⌐└A | +L, M2 | ||||
| FT1S+5=FT1N18 | 1 | i | i | переходник в двоичную, детектор 1 с true=1 false=-1 | F1ii(X) | 1ii | ∩↗A | └A | Negative Ternary Inverter (Mouftah), xi (Yoeli), decode-i | |||
| FT1S+6=FT1N19 | 1 | i | 0 | обмен 0 и −1 | F1i0(X) = «NOT2(Х)» = «NOT+1(x)» | 011 | swap 1/0 | swap 1/0 | /\' | |||
| FT1S+7=FT1N20 | 1 | i | 1 | переходник в двоичную, «инверсия Лукасевича» от детектора 0 | F1i1(X) | 1i1 | ∪↘∩A | |||||
| FT1S+8=FT1N21 | 1 | 0 | i | вращение нулевое, повторитель, Yes, тождественная функция, линия задержки, знак числа | F10i(X) = Sgn(X) | 101 | Buffer A | A | Buffer | |||
| FT1S+9=FT1N22 | 1 | 0 | 0 | переходник в двоичную | F100(X) | 100 | ∩↘A | ¬A | +R, M1 | |||
| FT1S+10=FT1N23 | 1 | 0 | 1 | переходник в двоичную | F101(X) | 101 | ↗∪A | |||||
| FT1S+11=FT1N24 | 1 | 1 | i | переходник в двоичную, «инверсия Лукасевича» от детектора −1 | F11i(X) | 11i | ∪↘A | ┘A | Positive Ternary Inverter | |||
| FT1S+12=FT1N25 | 1 | 1 | 0 | не циклический сдвиг вверх, не циклический сдвиг на +1 | F110(X) | 110 | ↗A = Shift Up,↗A | ¬┘A | Earthed Positive Ternary Inverter | M6 | ||
| FT1S+13=FT1N26 | 1 | 1 | 1 | переходник в +1, тождественная +1, тождественный максимум | F111(X) = 1 | 111 | always output 1 | |||||
Знаки «i», «1», «7» и «2» обозначают «-1».
По таблице видно, что при симметричном кодировании, функции являются теми же самыми, что и при несимметричном кодировании, только номера функций смещены на −13, и при замене знаков (-1,0,+1) на знаки (0,1,2) получается таблица унарных троичных функций в несимметричной троичной системе с соответствием (-1,0,+1) = (0,1,2).
Если знак «i» заменить на знак «2», то номера функций будут отличаться от номеров функций в таблице с несимметричным кодированием только на «вращение на 1 вперёд» несимметричного номера, то есть на функцию FT1N7 (RotF) от несимметричного номера.
Соответственно, что бы получить номер функции в таблице с несимметричным кодированием, в номере с симметричным кодированием нужно заменить знак «i» на знак «2» и взять от каждого его разряда троичную функцию «вращение на 1 назад» (FT1N11, RotB).
Троичная логическая тождественная функция
Троичный логический повторитель. Является простейшей линией задержки.
Обмены и вращения
Отрицание (инверсия, переворот, обращение) Not (Inv) существует только в чётных логиках: двоичной, четверичной, шестеричной и т. д.
В троичной логике вместо отрицания (инверсии, переворота, обращения) Not (Inv) существует пять подобных функций: три обмена — Swap и два вращения — Rot, которые не являются точными подобиями отрицания (инверсии), но немного похожи на отрицание (инверсию).
В восьмиричной логике обмен двух значений на восьмиричной окружности изменяет только два значения из восьми и очень мало похож на двоичную инверсию. Четыре циклических сдвига же на 1 шаг (Rot) на восьмиричной окружности делают полную инверсию всех восьми значений. Таким образом, почти полным подобием двоичной инверсии Not (вращению на 180°) в восьмиричной логике являются 4 циклических сдвига на 1 шаг (на 45°) влево или вправо (RotateLeft и RotateRight). Так же и в троичной логике подобиями двоичной инверсии Not являются циклические сдвиги влево и вправо на 1 шаг (на 120°) (RotateLeft и RotateRight), а не обмены только двух значений из всех трёх (Swap), с той лишь разницей, что в троичной логике, из-за шага 120°, нет такого подобия двоичной инверсии Not, как в восьмиричной и в других чётных логиках.
Во времена, когда этого не знали, сложились ошибочные названия типа «инверсия Лукасевича», которая, на самом деле, является центральным из трёх обменов — Swap+1/-1 и менее подобна двоичной инверсии Not, чем циклические сдвиги на 1 шаг влево и вправо (вращения на 120° влево и вправо, RotateLeft и RotateRight).
Обмены в троичной логике
Обмены — унарные операции, меняющие местами два из трёх логических состояний.
В отличие от двоичной логики, в которой есть только один обмен Swap0/+1, совпадающий с инверсией (отрицанием) Not, в троичной логике существуют три обмена[17]:
— FT1N19, FT1S+2, Swap0/+1 (обмен 0 и +1), («NOT-1»)
— FT1N15, FT1S-8, Swap+1/-1 (обмен +1 и −1), («NOT0», «NOTL» — «инверсия Лукасевича»)
— FT1N5, FT1S+6, Swap0/-1 (обмен 0 и −1), («NOT+1»)
Традиционный обмен Swap+1/-1 (называемый обращением или дополнением, неполным отрицанием), не влияющий на состояние «0» («неизвестно»), в некоторых статьях по троичной логике ошибочно называют «отрицанием Лукасевича» («инверсией Лукасевича») и обозначают как «~Lx» («NLx», «¬Lx», «x’L», «NOTL» или «NOT0»). Функция «инверсии (отрицания) Лукасевича» входит в логику Клини. Логика Лукасевича и логика Клини были ранними исследованиями троичных функций и не охватывали все троичные функции. Они являются усечёнными подмножествами общего множества простейших троичных функций.
Кроме традиционного обмена Swap+1/-1 («инверсия Лукасевича»), который сохраняет неизменным состояние 0 («неизвестно»), выделяют ещё две операции обмена, которые обозначают как Swap0/+1 («NOT-1») и Swap0/-1 («NOT+1»). Первый сохраняет неизменным состояние −1 («ложь»), а второй сохраняет +1 («истина»):
Таблица 5. (По этой таблице определяются номера Swap’ов в троичной симметричной системе кодирования.)
| y\x | +1 | 0 | -1 | |
|---|---|---|---|---|
| FT1S+2 | 0 | +1 | -1 | Swap0/+1, "NOT-1", обмен двух старших значений |
| FT1S-8 | -1 | 0 | +1 | Swap+1/-1, "NOT0", "NOTL", обмен двух крайних значений ("инверсия Лукасевича") |
| FT1S+6 | +1 | -1 | 0 | Swap0/-1, "NOT+1", обмен двух младших значений |
В троичной несимметричной системе кодирования возможны шесть соответствий троичной симметричной системе кодирования, но наиболее значимыми являются только два соответствия из шести: с заменой знака «-1» на «2» без циклического сдвига вперёд (вверх, вправо) на +1 (-1,0,+1)=(2,0,1) и с циклическим сдвигом вперёд (вверх, вправо) на +1 (-1,0,+1)=(0,1,2).
Эта же таблица, но с обозначениями (-1,0,+1)=(2,0,1) и с перебором значений аргумента: 2, 0, 1):
| y\x | 1 | 0 | 2 | |
|---|---|---|---|---|
| FT1S+2 | 0 | 1 | 2 | Swap01, обмен двух старших значений |
| FT1S-8 | 2 | 0 | 1 | Swap12, обмен двух крайних значений ("инверсия Лукасевича") |
| FT1S+6 | 1 | 2 | 0 | Swap02, обмен двух младших значений |
Эта же таблица в троичной несимметричной системе кодирования без сдвига, а только с заменой знака «-1» на «2» (-1,0,+1)=(2,0,1), но с перебором значений аргумента: 0, 1, 2 (по этой таблице определяются номера функций в троичной несимметричной системе кодирования) (в этой таблице «инверсия Лукасевича» уже является обменом двух старших значений, а не двух крайних значений, как в предыдущих таблицах, так же и две других функции обмена, но, для лучшего различения функций обмена лучше оставить названия их действий в троичной симметричной системе кодирования):
| y\x | 2 | 1 | 0 | |
|---|---|---|---|---|
| FT1N19=FT1S+2 | 2 | 0 | 1 | Swap01, обмен двух старших значений |
| FT1N15=FT1S-8 | 1 | 2 | 0 | Swap12, обмен двух крайних значений ("инверсия Лукасевича") |
| FT1N5=FT1S+6 | 0 | 1 | 2 | Swap02, обмен двух младших значений |
В таблице же в троичной несимметричной системе кодирования со сдвигом на RotR(X) (-1,0,+1)=(0,1,2), те же функции в таблице оказываются циклически сдвинутыми на одну строку, то есть «инверсией Лукасевича» уже является не FT1N15 (Swap12), а FT1N5 (Swap02), так же сдвинуты и две другие функции Swap:
| y\x | 2 | 1 | 0 | |
|---|---|---|---|---|
| FT1N15 | 1 | 2 | 0 | Swap12 (обмен двух старших значений) |
| FT1N5 | 0 | 1 | 2 | Swap02 (обмен двух крайних значений), ("инверсия Лукасевича") |
| FT1N19 | 2 | 0 | 1 | Swap01 (обмен двух младших значений) |
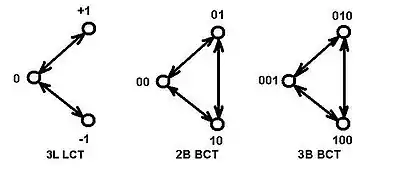
Граф операции Swap0/+1 («NOT-1») — одно ребро треугольника с двухсторонними переходами от 0 к +1 и обратно.
Граф переходов в операции Swap+1/-1 («инверсии Лукасевича») — одно ребро треугольника с двухсторонними переходами от +1 к −1 и обратно.
Граф операции Swap0/-1 («NOT+1») — одно ребро треугольника с двухсторонними переходами от 0 к −1 и обратно.
Все три операции линейные, одномерные, из линии в плоскость не выходят.
Закон двойного обмена справедлив для всех многозначных логик.
Для всех трёх обменов, как и для Swap0/+1(Swap01(X)) = X в двоичной логике, справедливы уравнения:
Swap0/+1(Swap0/+1(X)) = X
Swap+1/-1(Swap+1/-1(X)) = X
Swap0/-1(Swap0/-1(X)) = X
Вращения и инверсии
В двоичной логике вращение, отрицание, обращение, инверсия и негация совпадают и выражаются одной операцией вращения на 180° — этаким «5 в 1» NOT(X).
Точное подобие двоичной функции NOT(X) существует только в чётных многозначных логиках: четверичной, шестеричной, восьмиричной и т. д.
В троичной и более значных логиках вращения, отрицания, обращения, инверсии и негации являются разными функциями и не совпадают.
Вместо вращения на 180° (Not) в двоичной логике, в троичной логике существуют два вращения на 120°: RotLeft (-120°) и RotRight (+120°).
Так как электромеханические (реле) и электронные устройства (транзисторные каскады) переворачивают фазу на 180°, то они очень хорошо подошли для устройств двоичной логики. В троичной же логике нужны устройства поворачивающие фазу на 120°. Такие устройства относительно просто выполняются в механическом виде, но более сложно выполняются в электронном виде. Одним из решений этой задачи являются устройства выполненные в трёхбитной (3Bit BinaryCodedTernary, 3B BCT) системе троичных логических элементов[18].
В многозначных логиках
В двоичной логике существует закон двойного вращения на 1 шаг (180°) в одном направлении (двойного отрицания):
Not(Not(x)) = x
Rot(Rot(x)) = x
Направление вращения не различается. Из-за шага вращения 180° происходит занятие прямо противоположного положения на окружности (отрицание, обращение, инверсия и негация), поэтому функции Rot(x) (вращение), Not(x) (отрицание), Inv(x) (переворот) и Neg(x) совпадают.
В троичной логике существует закон тройного вращения на 1 шаг (120°) (циклического сдвига на 1 шаг) в одном направлении:
RotF(RotF(RotF(x))) = x
RotB(RotB(RotB(x))) = x
направление вращения различается, но занятия прямо противоположного положения на окружности (отрицания), из-за шага вращения 120°, не происходит, поэтому название Swap (обмен) для трёх известных троичных функций более точно, чем Not (отрицание) и Inv (переворот).
В четверичной логике существует закон четверного вращения на 1 шаг (90°) (циклического сдвига на 1 шаг) в одном направлении:
RotF(RotF(RotF(RotF(x)))) = x
RotB(RotB(RotB(RotB(x)))) = x
Направление вращения различается. Из-за шага вращения 90° возможно занятие прямо противоположного положения на окружности (Not (отрицание) и Inv (переворот)), но отрицание (Not) одно, а не три.
В пятиричной логике существует закон пятерного вращения на 1 шаг (72°) (циклического сдвига на 1 шаг) в одном направлении:
RotF(RotF(RotF(RotF(RotF(x))))) = x
RotB(RotB(RotB(RotB(RotB(x))))) = x
Направление вращения различается. Из-за шага вращения 72° занятие прямо противоположного положения на окружности (отрицание (Not) и переворот (Inv)) невозможны. …
В N-ичной логике существует закон N-го вращения на 1 шаг:
N вращений на 1 шаг в одном направлении равносильны повторению (утверждению).
В (N+1)-ичной логике существует закон (N+1)-го вращения:
(N+1) вращений на 1 шаг в одном направлении равносильны повторению (утверждению).
…
Обобщение:
В N-ичной плоской логике плоская логическая окружность делится на N частей, при этом N единичных вращений (вращений на 1 шаг (циклических сдвигов на 1 шаг)) в одном направлении по плоской логической окружности приводят в исходную точку.
Отрицания (Not) и инверсии (Inv) существуют только в чётных многозначных логиках.
В объёмных логиках место окружности занимают многомерные (в простейшем случае трёхмерные) сферы.
Вращения в троичной логике
Вращения (циклические сдвиги, отрицания, инверсии, обмены) вперёд и назад (вращение вверх и вращение вниз)[17].
Если рассмотреть многовершинные графы, то в них возможны вращение на 1 шаг вперёд (циклический сдвиг на 1 вперёд), вращение на 1 шаг назад (циклический сдвиг на 1 назад) и инверсии (перевороты).
Вращения не являются инверсиями и отличаются от функции обмена — Swap+1/-1 («инверсии (отрицания) Лукасевича») и от двух операций обмена — Swap0/+1 («инверсия NOT−1») и Swap0/-1 («инверсия NOT+1»). Они более просты и более полно описывают возможные переходы. В проекте Стива Грабба эти функции называются вращение вверх (RotU) и вращение вниз (RotD), кроме этого, их ещё называют вращением вперёд RotF и вращением назад RotB и вращением влево RotLeft и вращением вправо RotRight.
В троичной симметричной системе кодирования с обозначениями (-1,0+1)=(1,0,+1):
| y\x | 1 | 0 | 1 | |
|---|---|---|---|---|
| FT1S-6=FT1N7 | 1 | 1 | 0 | RotF, RotU |
| FT1S-2=FT1N11 | 0 | 1 | 1 | RotB, RotD |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
| y\x | 2 | 1 | 0 | |
|---|---|---|---|---|
| FT1N7 | 0 | 2 | 1 | RotF (Rotate Forward), RotU (Rotate Up) |
| FT1N11 | 1 | 0 | 2 | RotB (Rotate Back), RotD (Rotate Down) |
Для обеих функций справедливы уравнения:
RotF(RotF(RotF(x))) = x
RotB(RotB(RotB(x))) = x
которые являются законом тройного вращения:
три троичных вращения равносильны утверждению,
который является подобием закона двойного вращения в двоичной логике.
Только в троичной логике вращение на 2 шага вправо равно вращению на 1 шаг влево:
RotF(x) = RotB(RotB(x))
RotB(x) = RotF(RotF(x))
Следующие уравнения справедливы и в более, чем трёхзначной логиках:
Rot1B(Rot1F(x)) = x
Rot1F(Rot1B(x)) = x
Унарные троичные логические функции (операции, элементы) с бинарным результатом (выходом)
Всего существует простейших унарных троичных функций с бинарным выходом.
К этим функциям относятся демультиплексоры и дешифраторы с бинарным (двухразрядным) (результатом) выходом.
Унарные троичные логические функции (операции, элементы) с тринарным результатом (выходом)
Всего существует простейших унарных троичных функций с тринарным выходом.
К этим функциям относятся демультиплексоры и дешифраторы с тринарным (трёхразрядным) результатом (выходом).
Троичный дешифратор «1 трит в 3 строки»
Можно рассматривать как объединение трёх унарных троичных функций с унарными результатами из таблицы 1.
| y\x0=x | 2 | 1 | 0 | |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | FT1N1 |
| 1 | 0 | 1 | 0 | FT1N3 |
| 2 | 1 | 0 | 0 | FT1N9 |
Унарные троичные логические функции (операции, элементы) с m-арными выходами
Всего существует простейших унарных троичных функций с m-арным выходом, то есть бесконечное число.
К этим функциям относятся демультиплексоры и дешифраторы с m-арным (m-разрядным) результатом (выходом).
Бинарные троичные логические функции (операции, элементы)
Бинарные троичные логические функции с унарным результатом
Всего возможно простейших бинарных (двуместных, двухоперандных, двухаргументных, двухвходовых) троичных функций с унарным выходом, некоторые из них приведены в таблице:
Таблица некоторых бинарных троичных функций с унарным выходом с несимметричным кодированием
Таблица 5.
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | Название действия (функции) | Обозначение f(x,y) |
| FT2N010 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Тождественный ноль, тождественный минимум | FT2N0(x,y) = 0(x,y) = 0 |
| FT2N110 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | Троичная эмуляция двоичной 2ИЛИ-НЕ2, стрелки Пирса | FT2N1(x,y) = x↓2y |
| FT2N1810 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | Детектор (x-y)=2 (true=2, false=0) | |
| FT2N2110 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | ||
| FT2N3010 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | Троичная эмуляция двоичного сложения по модулю 2, XOR2 | FT2N30(x,y) = XOR2(x,y) |
| FT2N3110 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | Троичная эмуляция двоичной 2И-НЕ2, штриха Шеффера | FT2N31(x,y) = NAND2(x,y) = НЕ-И2(x,y) = Not2(Min2(x,y)) |
| FT2N8110 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | Троичная эмуляция двоичной 2-in AND2, 2И2, min2(x,y) | FT2N81(x,y) = min2(x,y) = AND2(x,y) = И2(x,y) |
| FT2N10910 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | Троичная эмуляция двоичной прямой (материальной) импликации, X <=2 Y | FT2N109(x,y) = IMP2(x,y) = (x LE2 y) |
| FT2N11110 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | Троичная эмуляция двоичной 2ИЛИ2, max2(x,y) | FT2N111(x,y) = max2(x,y) = OR2(x,y) = ИЛИ2(x,y) |
| FT2N11310 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 2 | Троичное подобие двоичной функции Вебба, по Полю Фальстаду CGOR[19] | FT2N113(x,y) = Swap20(Max(x,y)) |
| FT2N21010 | 0 | 0 | 0 | 0 | 2 | 1 | 2 | 1 | 0 | Сложение по модулю 3 при одном неполном слагаемом | |
| FT2N22310 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | 1 | Троичное подобие двоичной функции Вебба | FT2N223(x,y) = RotR(Max(x,y)) |
| FT2N24310 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | Разряд переноса при сложении с неполным слагаемым | |
| FT2N49210 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | детектор (x-y)=1 (true=2, false=0) | |
| FT2N51010 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 2 | 0 | x>y (true=2, false=0) | |
| FT2N56710 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | ||
| FT2N145810 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | Детектор x-y=-2 (true=2, false=0) | |
| FT2N262210 | 0 | 1 | 0 | 1 | 2 | 1 | 0 | 1 | 0 | Mean Function по Стиву Граббу[20] | x→y[21] |
| FT2N317010 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 2 | Троичное подобие двоичной функции Вебба | FT2N3170(x,y) = RotL(Max(x,y)) |
| FT2N404910 | 0 | 1 | 2 | 1 | 1 | 2 | 2 | 2 | 2 | CGAND[22] | FT2N4049(x,y) |
| FT2N442810 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | Детектор x-y=-1 (true=2, false=0) | FT2N4428(x,y) |
| FT2N529910 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | циклический сдвиг вправо (вперёд) на 1 (1/3 оборота) только одного второго аргумента (операнда) | FT2N5299(x,y) = RotR(x) |
| FT2N568110 | 0 | 2 | 1 | 2 | 1 | 0 | 1 | 0 | 2 | Младший разряд суммы (разности) в троичной симметричной системе счисления в соответствии {-1,0,+1}={0,1,2}, sum3s(x,y) | |
| FT2N588610 | 0 | 2 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | x<y (true=2, false=0) | |
| FT2N639610 | 0 | 2 | 2 | 2 | 0 | 2 | 2 | 2 | 0 | Детектор x≠y (true=2, false=0) | |
| FT2N715310 | 1 | 0 | 0 | 2 | 1 | 0 | 2 | 2 | 1 | Magnitude Function по Стиву Граббу[23] | |
| FT2N822910 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | Сложение по модулю 3 в симметричной системе с соответствием {-1,0,+1}={0,1,2}, SumMod3s(x,y) | |
| FT2N899110 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | Разряд переноса при бинарном сложении в несимметричной системе | FT2N8991(x,y) = Carry3n(x,y) |
| FT2N984110 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | Тождественная единица, тождественная середина | FT2N9841(x,y) = 1(x,y) = 1 |
| FT2N995110 | 1 | 1 | 1 | 1 | 2 | 2 | 1 | 2 | 0 | Троичное подобие двоичной функции Вебба | FT2N9951(x,y) = Swap21(Max(x,y)) |
| FT2N1320310 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | Разряд переноса при бинарном сложении в троичной симметричной системе счисления с соответствием {0,1,-1}={0,1,2} или {-1,0,+1}={2,0,1} | FT2N13203(x,y)= Carry3s(x,y) |
| FT2N1328610 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | x=y (true=2, false=0) | |
| FT2N1379610 | 2 | 0 | 0 | 2 | 2 | 0 | 2 | 2 | 2 | x>=y (true=2, false=0) | |
| FT2N1530910 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| FT2N1563310 | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | Минимум (меньшее из двух), Min Function по Стиву Граббу[24][25] | FT2N15633(x, y) = Min(x, y) |
| FT2N1567410 | 2 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | Троичная функция следования Брусенцова | F2TN15674(x,y) |
| FT2N1574010 | 2 | 1 | 0 | 1 | 2 | 0 | 2 | 2 | 2 | Импликация Гейтинга | FT2N15740(x, y) |
| FT2N1589710 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | повтор только первого аргумента (операнда) | FT2N15897(x,y) = Yes1(x,y) = x |
| F2TN1592910 | 2 | 1 | 0 | 2 | 1 | 1 | 2 | 2 | 2 | Импликация материальная | FT2N15929(x,y) |
| F2TN1601010 | 2 | 1 | 0 | 2 | 2 | 1 | 2 | 2 | 2 | Импликация Лукасевича | F2TN16010(x,y) |
| FT2N1640110 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | Разряд переноса при бинарном сложении-вычитании в симметричной троичной системе в соответствии {-1,0,+1}={0,1,2} | FT2N16401(x,y) = Carry3s(x,y) |
| FT2N1917210 | 2 | 2 | 2 | 0 | 2 | 2 | 0 | 0 | 2 | x<=y (true=2, false=0) | FT2N19172(x,y) |
| FT2N1930510 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | повтор только второго аргумента (операнда) | FT2N19305(x,y) = Yes2(x,y) = y |
| FT2N1945910 | 2 | 2 | 2 | 2 | 0 | 0 | 2 | 0 | 1 | Троичное подобие двоичной функции Вебба | FT2N19459(x,y) = Swap10(Max(x,y)) |
| FT2N1956910 | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 0 | Максимум (большее из двух), Max Function по Стиву Граббу[26][27] | FT2N19569(x, y) = Max(x, y) |
| FT2N1968210 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | Тождественная двойка, тождественный максимум | FT2N19682(x,y) = 2(x,y) = 2 |
Таблица некоторых бинарных троичных функций с унарным выходом с симметричным кодированием
Таблица 6.
| x0=x | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | i | i | i | Название действия (функции) | Обозначение |
| FT2S-9841 | i | i | i | i | i | i | i | i | i | Тождественная -1, тождественный минимум | F-9841(x,y) = -1 |
| FT2S-9618 | i | i | i | i | 1 | 1 | i | 1 | 0 | Функция Вебба | F-9618 = Webb(x,y) |
| FT2S-6388 | i | 0 | 0 | 1 | i | 0 | 1 | 1 | i | F-6388 | |
| FT2S-4542 | i | 1 | 0 | i | 1 | 0 | i | 1 | 0 | циклический сдвиг вперёд на 1/3 оборота только одного второго аргумента (операнда) | F-4542 = SHIFTF(X,Y) = SHIFTF(X) |
| FT2S-4160 | i | 1 | 0 | 1 | 0 | i | 0 | i | 1 | Младший разряд суммы (разности) при сложении в троичной симметричной системе счисления, sum3s(x,y) | F-4160 |
| FT2S-3700 | i | 1 | 1 | 0 | i | 1 | 0 | 0 | i | F-3700 | |
| FT2S-3445 | i | 1 | 1 | 1 | i | 1 | 1 | 1 | i | x≠y, notL(x=y), детектор x≠y (true=+1 и false=-1) | F-3445 |
| FT2S-2688 | 0 | i | i | 1 | 0 | i | 1 | 1 | 0 | sign(y-x), Magnitude Function Стива Грабба[23] | F-2688 = sign(y-x) |
| FT2S-1612 | 0 | i | 1 | i | 1 | 0 | 1 | 0 | i | Сложение по модулю 3 в несимметричной системе, summod3n(x,y) | F-1612 |
| FT2S-850 | 0 | 0 | i | 0 | i | i | i | i | i | Разряд переноса при бинарном сложении в несимметричной системе | F-850 |
| F2TS0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Тождественный ноль, тождественная середина | F0(x,y) = 0 |
| FT2S2688 | 0 | 1 | 1 | i | 0 | 1 | i | i | 0 | notL(sign(y-x)), инверсия Лукасевича от Magnitude Function по Стиву Граббу | F2688 |
| FT2S3700 | 1 | i | i | 0 | 1 | i | 0 | 0 | 1 | F3700 | |
| FT2S3955 | 1 | i | i | 1 | 1 | i | 1 | 1 | 1 | (x<y, notL(x>y)) (true=+1 и false=-1) | F3955 |
| FT2S5792 | 1 | 0 | i | 0 | 0 | i | i | i | i | Меньшее из двух, минимум | F5792 = min(x,y) |
| FT2S5833 | 1 | 0 | i | 0 | 0 | 0 | 0 | 0 | 1 | Троичная функция следования Брусенцова | F5833 |
| FT2S6056 | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | повтор только второго аргумента (операнда) | F6056 = YES1(x,y) = x |
| FT2S6088 | 1 | 0 | i | 1 | 0 | 0 | 1 | 1 | 1 | Импликация материальная | F6088 |
| FT2S6142 | 1 | 0 | i | 1 | 1 | i | 1 | 1 | 1 | Импликация Гейтинга | F6142 |
| FT2S6169 | 1 | 0 | i | 1 | 1 | 0 | 1 | 1 | 1 | Импликация Лукасевича | F6169 |
| FT2S6388 | 1 | 0 | 0 | i | 1 | 0 | i | i | 1 | F6388 | |
| FT2S6550 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | i | Разряд переноса при бинарном сложении в симметричной троичной системе | F6560 |
| FT2S9331 | 1 | 1 | 1 | i | 1 | 1 | i | i | 1 | x>y, notL(x-y) (true=+1 и false=-1) | F9331 |
| FT2S9464 | 1 | 1 | 1 | 0 | 0 | 0 | i | i | i | повтор только первого аргумента (операнда) | F9464 = YES2(x,y) = y |
| FT2S9728 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | i | Большее из двух, максимум | F9728 = max(x,y) |
| FT2S9841. | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | Тождественная +1, тождественный максимум | F9841(x,y) = 1 |
«i», «1», «7» или «2» означают «-1»
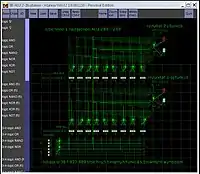
Все 19 683 простейшие троичные бинарные функции выполняются троичным АЛУ (2Трита в 1Трит) в трёхбитной одноединичной системе троичных логических элементов, снимок модели которого в логическом симуляторе Atanua приведён на рисунке.
Троичная эмуляция двоичной 2ИЛИ-НЕ (стрелки Пирса)
Троичная эмуляция двоичной бинарной функции 2ИЛИ-НЕ (стрелка Пирса).
Результат является двоичным.
В троичной несимметричной системе кодирования с обозначениями (-1,0,1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 0 0 0 0 - 1 0 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N110 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | FT2N1 = x↓y |
Троичная эмуляция двоичного сложения по модулю 2, XOR
Троичная эмуляция двоичной функции «бинарное сложение по модулю 2», XOR.
Результат является двоичным.
В троичной несимметричной системе кодирования с обозначениями (-1,0,1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 0 1 0 0 - 0 1 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N3010 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | FT2N30 = XOR(x,y) |
Троичная эмуляция двоичной 2И-НЕ (штриха Шеффера)
Троичная эмуляция двоичной бинарной функции 2И-НЕ (штриха Шеффера).
Результат является двоичным.
В троичной несимметричной системе кодирования с обозначениями (-1,0,1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 0 1 0 0 - 1 1 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N3110 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | FT2N31 = NAND(x,y) = НЕ-И(x,y) = Not(Min(x,y)) |
Троичная эмуляция двоичной 2И, min(x, y)
Троичная эмуляция двоичной бинарной функции 2-in AND, 2И, min(x, y).
Результат является двоичным.
В троичной несимметричной системе кодирования с обозначениями (-1,0,1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 0 0 1 0 - 0 0 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N8110 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | FT2N81 = min(x,y) = AND(x,y) = И(x,y) |
Троичная эмуляция двоичной прямой (материальной) импликации, x <= y
Троичная эмуляция двоичной бинарной функции «прямая (материальная) импликация», x <= y.
Результат является двоичным.
В троичной несимметричной системе кодирования с обозначениями (-1,0,1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 0 1 1 0 - 1 0 0 -> x |
На диаграмме хорошо видна несимметричность функции.
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N10910 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | FT2N109 = IMP(x,y) = (x LE y) |
Троичная эмуляция двоичной 2ИЛИ, max(x, y)
Троичная эмуляция двоичной бинарной функции 2-in OR, 2ИЛИ, max(x, y).
Результат является двоичным.
В троичной несимметричной системе кодирования с обозначениями (-1,0,1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 0 1 1 0 - 0 1 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N11110 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | FT2N111 = max(x,y) = OR(x,y) = ИЛИ(x,y) |
Больше
Результат по сути является двоичным.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
Истинно=1, ложно=1.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 1
- 1 1 1 -> x
1 1 1
|
На диаграмме хорошо видна несимметричность функции по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S-933110 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | x>y |
В троичной симметричной системе счисления с обозначениями (-1,0,+1)=(2,0,1):
Истинно=1, ложно=2 (-1).
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
2 2 2
- 2 2 1 -> x
2 1 1
|
В виде таблицы истинности:
| x0=x | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | |
| FT2N1942710 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 1 | 2 | x>y |
В троичной несимметричной системе счисления с обозначениями (-1,0,+1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 0 0 0 2 - 0 2 2 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N51010 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 2 | 0 | x>y |
Больше либо равно
Результат по сути является двоичным.
В троичной симметричной системе кодирования с обозначениями (-1,0,1)=(1,0,1):
Истинно=1, ложно=1.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 1
- 1 1 1 -> x
1 1 1
|
На диаграмме хорошо видна несимметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S395510 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | x>=y |
В троичной несимметричной системе кодирования с обозначеениями (-1,0,1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 2 0 2 2 - 2 2 2 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N1379610 | 2 | 0 | 0 | 2 | 2 | 0 | 2 | 2 | 2 | x>=y |
Меньше
Результат по сути является двоичным.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
Истинно=1, ложно=1.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 1
- 1 1 1 -> x
1 1 1
|
На диаграмме хорошо видна несимметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S-395510 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | x<y |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 2 2 0 2 0 0 - 0 0 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N588610 | 0 | 2 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | x<y |
Меньше либо равно
Результат по сути является двоичным.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
Результат по сути является двоичным.
Истинно=1, ложно=1.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 1
- 1 1 1 -> x
1 1 1
|
На диаграмме хорошо видна несимметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S933110 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | x<=y |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
Истинно=2, ложно=0.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 2 2 2 2 2 0 - 2 0 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N1917210 | 2 | 2 | 2 | 0 | 2 | 2 | 0 | 0 | 2 | x<=y |
Равно
Вычисляется eqv(x, y); x eqv y.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
Результат по сути является двоичным.
Истинно — 1, ложно — 1.
В виде двухмерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 1
- 1 1 1 -> x
1 1 1
|
На диаграмме хорошо видна симметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S3445 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | x=y |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
При обозначениях результата: истинно=2, ложно=0.
В виде двухмерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 2 0 2 0 - 2 0 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N1328610 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | x=y |
В виде матрицы
Троичная функция отношения
Троичный компаратор с унарным троичным выходом.
Magnitude Function по Стиву Граббу[23]
С однозначным результатом[28]
Определяет отношения тритов в разрядах.
Кроме равенства Лукасевича, которое имеет двоичный результат и подобно двоичному равенству, в общей троичной логике появляются троичные функции отношения, которые сразу определяют три возможных отношения операндов — меньше, равно или больше. Так как в двоичной логике результат может принимать только два значения, то в двоичной логике таких функций нет.
Результат изменяется при перемене мест операндов.
В зависимости от порядка следования отношений в результате, может быть несколько разновидностей этой функции. Например (<,=,>), (>,=,<) и экзотические (<,>,=), (>,<,=), (=,<,>) и др.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
С обозначениями результата (x<y,x=y,x>y) = (<,=,>) = (1,0,1).
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 0
- 1 0 1 -> x
0 1 1
|
На диаграмме хорошо видна несимметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S-268810 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | sign(y-x) |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
С обозначениями результата (x<y,x=y,x>y) = (<,=,>) = (0,1,2).
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 1 0 1 2 - 1 2 2 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-й операнд |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-й операнд |
| FT2N715310 | 1 | 0 | 0 | 2 | 1 | 0 | 2 | 2 | 1 | F(x,y) |
Троичный компаратор с тринарным двоичным выходом
Сравнивает поразрядно триты двух чисел и имеет тринарный двоичный выход: меньше, равно, больше. Является объединением трёх предыдущих отдельных троичных бинарных функций.
Результат изменяется при перемене мест операндов.
true=2, false=0
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-й операнд |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-й операнд |
| x<y | 0 | 2 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | |
| x=y | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | |
| x>y | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 2 | 0 |
Минимум (наименьшее)
Вычисляется min(x,y).
В двоичной логике функции min(x, y) соответствует конъюнкция: x ∧ y, x И y, 2И.
Входит в логику Клини.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 0 1
- 1 0 0 -> x
1 1 1
|
На диаграмме хорошо видна симметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x1=y | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x0=x | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S5792(x,y) | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | min(x,y) |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 1 2 0 1 1 - 0 0 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N1563310 | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | min(x,y) |
Максимум (наибольшее)
Вычисляется max(x, y).
В двоичной логике функции max(x, y) соответствует дизъюнкция: x ∨ y, x ИЛИ y, 2ИЛИ(x, y).
Входит в логику Клини.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 1
- 0 0 1 -> x
1 0 1
|
На диаграмме хорошо видна симметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S972810 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | max(x,y) |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 2 2 2 1 1 2 - 0 1 2 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N1956910 | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 0 | max(x,y) |
В виде матрицы
Сложение по модулю 3 в несимметричной троичной системе счисления
Вычисляется сумма по модулю 3: x MOD3 y, MOD3(x, y,).
Аналог сложения по модулю 2. Название «исключающее ИЛИ» («XOR»), применяемое для «двоичного сложения по модулю 2», для «троичного сложения по модулю 3» неприемлемо, то есть оказалось поверхностным, не глубоким.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 0
- 0 1 1 -> x
1 0 1
|
На диаграмме хорошо видна симметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S-161210 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | x MOD3 y, MOD3(x,y) |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 2 0 1 1 2 0 - 0 1 2 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N822910 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | x MOD3 y, MOD3(x,y) |
В виде матрицы
Сложение по модулю три напоминает двоичный XOR. Это обычное сложение, только без переноса: в случае переполнения разрядной сетки оно сохраняет лишь младший троичный разряд. Как и двоичный XOR, сложение по модулю три либо оставляет троичный разряд неизменным, либо изменяет его (производит операции RotF/RotB, в зависимости от знака соответствующего троичного разряда).
Эта функция может быть полезна для реализации троичных несимметричных полусумматора и сумматора.
Разряд переноса при бинарном (двухаргументном, двухоперандном) сложении в троичной несимметричной системе счисления
То есть разряд переноса при троичном несимметричном сложении в троичном несимметричном полусумматоре.
В троичной симметричной системе кодирования обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 0 0
- 1 1 0 -> x
1 1 1
|
На диаграмме хорошо видна симметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S-85010 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 1 1 0 0 1 - 0 0 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| FT2N899110 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
В виде матрицы
Младший разряд результата в троичном симметричном сложении
То есть младший разряд в троичном симметричном полусумматоре.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
0 1 1
- 1 0 1 -> x
1 1 0
|
На диаграмме хорошо видна симметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S-416010 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | Младший разряд в троичном симметричном полусумматоре |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 1 2 0 0 1 2 - 2 0 1 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| FT2N568110 | 0 | 2 | 1 | 2 | 1 | 0 | 1 | 0 | 2 | Младший разряд в троичном симметричном полусумматоре |
Трит переноса при бинарном (двухаргументном, двухоперандном) сложении при троичном симметричном сложении
То есть трит переноса в троичном симметричном полусумматоре.
В троичной симметричной системе кодирования с обозначениями (-1,0,1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
0 0 1
- 0 0 0 -> x
1 0 0
|
На диаграмме хорошо видна симметричность по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| FT2S656010 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | Трит переноса в троичном симметричном полусумматоре |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 1 1 2 1 1 1 - 0 1 1 -> x |
Троичное умножение
В троичной несимметричной системе (-1,0,+1)=(0,1,2):
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | Умножаемое |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | Множитель |
| FT2N1150210 | 1 | 2 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | Младший трит результата |
| FT2N656110 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Старший трит результата (трит переноса) |
Перенос возникает в одном случае из девяти.
В виде двух двумерных (двухаргументных, двухкоординатных) диаграмм:
FT2N11502 FT2N6561 y y ^ ^ | | 0 2 1 0 0 1 0 1 2 0 0 0 - 0 0 0 -> x - 0 0 0 -> x | |
В троичной симметричной системе (-1,0,+1)=(2,0,1):
В виде таблицы истинности:
| x0=x | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | Умножаемое |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | Множитель |
| FT2N803810 | 1 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 1 | Трит результата |
Перенос не возникает вовсе.
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
FT2N8038
y
^
|
2 0 1
- 0 0 0 -> x
1 0 2
|
Импликации
Импликация (от лат. implicatio — сплетение, implico — тесно связываю) — логическая связка, соответствующая грамматической конструкции «если …, то …», с помощью которой из двух простых высказываний образуется сложное высказывание. В импликативном высказывании различают антецедент (основание) — высказывание, идущее после слова «если», и консеквент (следствие) — высказывание, идущее за словом «то». Импликативное высказывание представляет в языке логики условное высказывание обычного языка. Последнее играет особую роль как в повседневных, так и в научных рассуждениях, основной его функцией является обоснование одного путём ссылки на нечто другое. В современной логике имеется большое число импликаций, различающихся своими формальными свойствами:
- Троичная функция следования Брусенцова
- импликация материальная
- импликация Гейтинга
- импликация Лукасевича
Троичная функция следования Брусенцова
Вычисляется :
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 0 1
- 0 0 0 -> x
1 0 0
|
На двумерной (двухаргументной, двухкоординатной) диаграмме хорошо видно, что Функция несимметрична, то есть при перемене мест аргументов результат изменяется.
В виде таблицы истинности:
| x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2-е высказывание |
| FT2S583310 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | Троичная функция следования Брусенцова |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1) = (0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 1 2 1 1 1 - 2 1 1 -> x |
В виде таблицы истинности:
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е высказывание |
| FT2N1567410 | 2 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | Троичная функция следования Брусенцова |
Импликация материальная
Материальная импликация — одна из основных связок классической логики. Определяется она таким образом: импликация ложна только в случае истинности основания (антецедента) и ложности следствия (консеквента), а истинна во всех остальных случаях. Условное высказывание «если x, то y» предполагает некоторую реальную связь между тем, о чём говорится в x и y; выражение «x материально имплицирует y» такой связи не предполагает.
Вычисляется материальная импликация: max(x,-y); ; x ∨ -y.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1) = (1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 0 1
- 0 0 1 -> x
1 1 1
|
На двумерной (двухаргументной, двухкоординатной) диаграмме хорошо видно, что функция несимметрична по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат изменяется, но симметрична по отношению к обратной (с наклоном влево) диагонали.
В виде таблицы истинности:
| x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2-е высказывание |
| FT2S608810 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | Импликация материальная |
В троичной несимметричной системе кодирования с обозначениями {-1,0,+1} = {0,1,2}:
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 1 2 1 1 2 - 2 2 2 -> x |
В виде таблицы истинности:
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е высказывание |
| FT2N1592910 | 2 | 1 | 0 | 2 | 1 | 1 | 2 | 2 | 2 | Импликация материальная |
Импликация Гейтинга
Это часть многозначной логики.
Логика Гейтинга охватывала лишь часть классической формальной логики.
Импликацию (если р, то q) можно утверждать, только если имеется такое построение, которое, будучи объединено с построением р, автоматически даёт построение q. Например, из истинности высказывания p следует «неверно, что p ложно». Но из утверждения «неверно, что p ложно» ещё не следует, что p — истинно, так как высказывание p может оказаться неконструктивным.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1) = (1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 0 1
- 1 1 1 -> x
1 1 1
|
Функция несимметрична по отношению к главной диагонали, что хорошо видно на двухаргументной (двухоперандной, двухкоординатной) диаграмме, то есть при перемене мест операндов результат изменяется.
В виде таблицы истинности:
| x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2-е высказывание |
| FT2S-984110 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | Импликация Гейтинга |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1) = (0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 1 2 0 2 2 - 2 2 2 -> x |
В виде таблицы истинности:
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е высказывание |
| FT2N1574010 | 2 | 1 | 0 | 1 | 2 | 0 | 2 | 2 | 2 | Импликация Гейтинга |
Импликация Лукасевича
[29][30] Это часть модальной логики.
В троичной симметричной системе кодирования с обозначениями (-1,0,+1) = (1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 0 1
- 0 1 1 -> x
1 1 1
|
Функция не симметрична по отношению к главной (с наклоном вправо) диагонали, что хорошо видно на двухаргументной (двухоперандной, двухкоординатной) диаграмме, то есть при перемене мест аргументов результат изменяется, но симметрична по отношению к обратной (с наклоном влево) диагонали.
В виде таблицы истинности:
| x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2-е высказывание |
| FT2S616910 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | Импликация Лукасевича |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1) = (0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 1 2 1 2 2 - 2 2 2 -> x |
В виде таблицы истинности:
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е высказывание |
| FT2N1601010 | 2 | 1 | 0 | 2 | 2 | 1 | 2 | 2 | 2 | Импликация Лукасевича |
Сложение по модулю 3 при одном неполном слагаемом
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 1 2 0 - 0 1 2 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 1-е слагаемое |
|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 2-е слагаемое |
| FT1B1N21010 | 0 | 2 | 1 | 2 | 1 | 0 | Сумма по модулю 3 |
В виде матрицы:
Разряд переноса при сложении с неполным слагаемым
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 1 - 0 0 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 1-е слагаемое |
|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 2-е слагаемое |
| FT1B1N24310 | 1 | 0 | 0 | 0 | 0 | 0 | Перенос в n+1 |
В виде матрицы:
Троичные подобия двоичной функции Вебба
В троичной логике двоичной функции max(x, y) (OR, V) соответствует троичная функция max(x, y), которая уже не является функцией OR (V).
Так как вращению на 180° — Rot (перевороту, отрицанию, инверсии, негации) (Rot, Not, Inv, Neg) в двоичной логике в троичной логике соответствуют три функции обмена — Swap и две функции вращения — Rot, то в троичной логике существуют пять троичных подобий двоичной функции Вебба равной Not(max(x, y)).
Троичное подобие двоичной функции Вебба со Swap0/+1
Вычисляется: троичное подобие двоичной функции Webb со Swap0/+1 = Swap0/+1(max(x, y)).
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
0 0 0
- 1 1 0 -> x
1 1 0
|
На диаграмме хорошо видно, что функция симметрична по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2-е высказывание |
| FT2S11010 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | подобие Webb со Swap0/+1 = Swap0/+1(max(x,y)) |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 1 1 1 2 2 1 - 0 2 1 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е высказывание |
| FT2N995110 | 1 | 1 | 1 | 1 | 2 | 2 | 1 | 2 | 0 | подобие Webb со Swap2/1 = Swap2/1(max(x,y)) |
В виде матрицы
Троичное подобие двоичной функции Вебба со Swap+1/-1
Вычисляется: троичное подобие двоичной функции Webb со Swap+1/-1 = Swap+1/-1(max(x, y)).
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 1
- 0 0 1 -> x
1 0 1
|
На диаграмме хорошо видно, что функция симметрична по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2-е высказывание |
| FT2S-972810 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | подобие Webb со Swap+1/-1 = Swap+1/-1(max(x,y)) |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 0 1 1 0 - 2 1 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е высказывание |
| FT2N11310 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 2 | подобие Webb со Swap2/0 = Swap2/0(max(x,y)) |
В виде матрицы
Троичное подобие двоичной функции Вебба со Swap0/-1
Вычисляется: троичное подобие двоичной функции Webb со Swap0/-1 = Swap0/-1(max(x, y)).
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 1
- 1 1 1 -> x
0 1 1
|
На диаграмме хорошо видно, что функция симметрична по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2-е высказывание |
| FT2S961810 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | подобие Webb со Swap0/-1 = Swap0/-1(max(x,y)) |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 2 2 2 0 0 2 - 1 0 2 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е высказывание |
| FT2N1945910 | 2 | 2 | 2 | 2 | 0 | 0 | 2 | 0 | 1 | Webb(Swap1/0)(x,y) = Swap1/0(max(x,y)) |
В виде матрицы
Троичное подобие двоичной функции Вебба с RotF
Вычисляется: троичное подобие двоичной функции Webb с RotF = RotF(max(x, y)).
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
1 1 1
- 1 1 1 -> x
0 1 1
|
На диаграмме хорошо видно, что функция симметрична по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2-е высказывание |
| FT2S-961810 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | подобие Webb c RotF = RotF(max(x,y)) |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 0 0 0 2 2 0 - 1 2 0 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е высказывание |
| FT2N22310 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | 1 | подобие Webb с RotF(x,y) = RotF(max(x,y)) |
В виде матрицы
В двоичной логике функция Вебба обозначается стрелкой Пирса (↓) и определяется, как антидизъюнкция Webb(x, y) = x ↓ y = Not(x OR y) = Not(max(x, y)).
Автор же статьи «Сведения по трёхзначной логике»[31] обозначает троичное подобие двоичной функции Вебба штрихом Шеффера, которым в двоичной логике обозначают антиконъюнкцию, которая равна Sheff(x, y) = x | y = Not(x AND y) = Not(min(x, y)).
Автор статьи даёт определение трёхзначной функции Вебба, как Webb(a, b) = a | b = mod3(max(a, b) + 1)) (7) = RotF(max(a, b)), хотя в двоичной логике функцию Вебба обозначают стрелкой Пирса, а не штрихом Шеффера, а при обозначении штрихом Шеффера двоичная функция явяляется антиконъюнкцией, а не функцией Вебба (антидизъюнкцией), и равна Not(min(a, b)) = Not(a AND b), а не Not(max(a, b)) = Not(a OR b), но в первой части функции автор вычисляет max(a, b), то есть вместо стрелки Пирса (↓) поставил штрих Шеффера (|), но вычислял a OR b = max(a, b), а не a AND b = min(a, b). Во второй части функции автор мудрёным способом вычисляет одно из пяти троичных подобий двоичной инверсии (отрицания, негации) — RotF и почему то считает функцию FT2N223 единственной представительницей троичных подобий функции Вебба из пяти троичных подобий двоичной функции Вебба, хотя функция FT2N113(x, y) = Swap2/0(max(x, y)) более веббистая, чем FT2N223.
Троичное подобие двоичной функции Вебба с RotB
Вычисляется: троичное подобие двоичной функции Webb с RotB = RotB(max(x, y)).
В троичной симметричной системе кодирования с обозначениями (-1,0,+1)=(1,0,1):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y
^
|
0 0 1
- 1 1 0 -> x
1 1 0
|
На диаграмме хорошо видно, что функция симметрична по отношению к главной (с наклоном вправо) диагонали, то есть при перемене мест аргументов результат не изменяется.
В виде таблицы истинности:
| x0=x | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 2-е высказывание |
| FT2S-667110 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | подобие Webb с RotB = RotB(max(x,y)) |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде двумерной (двухаргументной, двухкоординатной) диаграммы:
y ^ | 1 1 0 0 0 1 - 2 0 1 -> x |
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е высказывание |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е высказывание |
| FT2N317010 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 2 | подобие Webb с RotB = RotB(max(x,y)) |
В виде матрицы
Рассуждения на тему функции Вебба
Функция Вебба интересна тем, что с помощью неё, подобно штриху Шеффера и стрелке Пирса в двухзначной логике, можно выразить любые трёхзначные функции:
Одноместные:
- RotF(X) = X | X
/* Результат двухместной (двухоперандной) операции может быть равен результату одноместной (одноаргументной) функции, но из этого не следует равенства самой одноместной функции и двухместной (двухоперандной) операции. RotF(X) и RotB(X) - функции одноместные (одноаргументные), а троичное подобие двоичной двухместной (двухаргументной, двухоперандной) функции Вебба или оператора Вебба должно быть, как и в двоичной логике двухместным (двухаргументным, двухоперандным). Вообще же, для того, что хотят выразить с помощью троичной логики, лучше подходит четверичная или восмиричная логики, у троичной же логики другое назначение. */
- RotB(X) = RotF(RotF(X),RotF(X)) = (X | X) | (X | X)
/* RotF(X) - функция одноместная (одноаргументная, однооперандная), автор же использует её, как двухместную (двухаргументную, двухоперандную). */
- NOT(X) = (RotB(X) | RotF(X) | RotF(RotB(X) | X))
/* Двоичная операция 2И-НЕ (штрих Шеффера - "|") невозможна с троичными операндами RotB и RotF. Определения же троичного подобия двоичной функции 2И-НЕ (штриху Шеффера - "|") автор не дал. */
Двухместные:
- X ∨ Y = RotB(X | Y)
/* Прежде, чем брать функцию RotB() нужно дать определение троичного подобия двоичной функции 2И-НЕ (штриху Шеффера). */
- X ∧ Y = Not(Not(X) ∨ Not(Y))
/* Прежде, чем брать двоичную функцию Not() от подразумеваемого троичного результата нужно дать определение троичного подобия двоичной функции 2ИЛИ-НЕ (стрелке Пирса) или дать определение троичному подобию двоичной функции Not(). */
Вполне возможно, что именно логическим элементам, реализующим функцию Вебба, придётся сыграть роль троичных ЛА3’их (ИС SN7400, 4 логических элемента 2И-НЕ[32]). И от качества реализации этой функции, количества транзисторов, будет зависеть эффективность будущих троичных процессоров.
/* В троичной трёхуровневой системе троичных логических элементов (3-Level LevelCodedTernaty, 3L LCT) при переходах из состояния +1 в состояние -1 и наоборот потенциал (напряжение) проходит через состояние 0, что неизбежно приводит к ложным срабатываниям и низкому качеству реализации троичных функций. В троичной двухуровневой трёхбитной одноединичной системе троичных логических элементов (2-Level 3-Bit BinaryCodedTernary UnoUnary, 2L 3B BCT UU, 2L 3B BCT, 3B BCT) в каждой отдельной линии фаза переворачивается на ±180° и физических поворотов фазы на +120° и -120° нет, но все три состояния логически распознаются и эта система может быть логическим подобием троичной системы с поворотами на +120° и -120°. При любых переходах перехода через третье состояние не происходит, что повышает качество реализации троичных функций.*/
Впрочем, функция RotB(X ∨ Y) (а возможно, что и RotF(X ∧ Y), RotB(X ∧ Y) ничем не хуже. Вопрос лишь в том, какую из них мы сможем реализовать наиболее эффективно.
/* Чтобы сделать троичное подобие двоичного поворота на ±180° (Not(X)), автор из пяти троичных подобий двоичного Not(X) выбрал только поворот на -120° (RotB()), который более подобен двоичному повороту на ±180° (Not), чем неполные обмены только двух значений из трёх (Swap'ы), но поворот на +120° (RotF()) не хуже поворота на -120° (RotB()), о чём и пишет автор. */
Бинарные троичные логические функции (операции, элементы) с бинарным выходом
Всего возможно простейших бинарных с бинарным выходом троичных функций (2Трита-2Трита).
Все 387 420 489 простейших троичных бинарных с бинарным выходом функций выполняются АЛУ в трёхбитной одноединичной системе троичных логических элементов, приведённым на рисунке справа.
Троичный полусумматор с одним неполным слагаемым
Первая ступень трёхступенчатого полного троичного сумматора.
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1)=(0,1,2):
В виде таблицы исстинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | полное слагаемое |
|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | неполное слагаемое |
| FT1B1N21010 | 0 | 2 | 1 | 2 | 1 | 0 | Сумма по модулю 3 |
| FT1B1N24310 | 1 | 0 | 0 | 0 | 0 | 0 | Перенос в n+1 |
Результат операции занимает 1 и 2/3 троичных разряда.
Бинарное сложение в несимметричной троичной системе счисления (троичный полусумматор)
Бинарное (двухаргументное, двухоперандное) сложение в троичной несимметричной системе счисления, то есть троичный несимметричный полусумматор.
Троичный полусумматор можно рассматривать, как объединение двух бинарных (двухаргументных, двухоперандных) троичных функций: «сложение по модулю 3 в троичной несимметричной системе счисления» и «разряд переноса при сложении в троичной несимметричной системе счисления».
Так как при сложении в троичной несимметричной системе в разряде переноса не бывает значения больше единицы, то, в отличие от предыдущих бинарных троичных функций с одноразрядным результатом, бинарный результат функции занимает 1 и 1/3 троичных разрядов.
Результат не изменяется при перемене мест аргументов.
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е слагаемое |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е слагаемое |
| FT2N822910 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | Сумма по модулю 3, несимметричная; x SUMMOD3 y, SUMMOD3(x,y) |
| FT2N899110 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | Перенос в n+1, несимметричный |

или в виде матрицы
Бинарное сложение-вычитание в троичной симметричной системе счисления Фибоначчи
Троичный полусумматор-полувычитатель.
Троичное логическое сложение-вычитание двух троичных разрядов с разрядом переноса в троичной симметричной системе счисления.
Результат не изменяется при перемене мест операндов.
Троичный полусумматор-полувычитатель можно рассматривать, как объединение двух бинарных (двухаргументных, двухоперандных) троичных функций: «младший разряд суммы при сложении-вычитании в троичной симметричной системе счисления» и «разряд переноса при бинарном (двухаргументном, двухоперандном) сложении-вычитании в троичной симметричной системе счисления».
В отличие от сложения и вычитания в троичной несимметричной системе счисления, результат функции занимает 2 полных троичных разряда (трита), так как при сложении-вычитании в троичной симметричной системе в разряде переноса бывают все три значения трита.
В троичной симметричной системе кодирования с обозначениями (−1, 0, +1) = (i, 0, 1):
В виде двух двухаргументных (двухоперандных, двухкоординатных) диаграмм:
FT2S-4160 FT2S6560
y y
^ ^
| |
0 1 1 0 0 1
- 1 0 1 -> x - 0 0 0 -> x
1 1 0 1 0 0
| |
В виде одной двухаргументной (двухоперандной, двухкоординатной) диаграммы:
y
^
|
00 01 11
- 01 00 01 -> x
11 01 00
|
В виде таблицы истинности:
| x0=x | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | 1-е слагаемое-уменьшаемое |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | i | i | i | 2-е слагаемое-вычитаемое |
| FT2S-416010 | i | 1 | 0 | 1 | 0 | i | 0 | i | 1 | Младший разряд (трит) симметричной суммы |
| FT2S656010 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | i | Старший разряд (трит) симметричной суммы, трит переноса в n+1 разряд |
В виде матрицы
В троичной симметричной системе кодирования с обозначениями (-1,0,+1) = (2,0,1):
В виде двух двухаргументных (двухоперандных, двухкоординатных) диаграмм:
FT2N15613 FT2N6563
y y
^ ^
| |
0 1 2 0 0 1
- 2 0 1 -> x - 0 0 0 -> x
1 2 0 2 0 0
| |
В виде одной двухаргументной (двухоперандной, двухкоординатной) диаграммы:
y
^
|
00 01 12
- 02 00 01 -> x
21 02 00
|
В виде таблицы истинности:
| x0=x | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1-е слагаемое-вычитаемое |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 2-е слагаемое-вычитаемое |
| FT2N1561310 | 2 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 1 | Младший разряд (трит) симметричной суммы |
| FT2N656310 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | Старший разряд (трит) симметричной суммы, трит переноса в n+1 разряд |
В троичной несимметричной системе кодирования с обозначениями (-1,0,+1) = (0,1,2):
В виде двухаргументной (двухоперандной, двухкоординатной) диаграммы:
y
^
|
11 12 20
- 10 11 12 -> x
02 10 11
|
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е слагаемое-вычитаемое |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е слагаемое-вычитаемое |
| FT2N568110 | 0 | 2 | 1 | 2 | 1 | 0 | 1 | 0 | 2 | Младший разряд (трит) симметричной суммы |
| FT2N1640110 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | Старший разряд (трит) симметричной суммы, трит переноса в n+1 разряд |

В виде матрицы
Бинарные троичные логические функции с нонарным результатом (выходом)
Всего возможно ≈ простейших бинарных троичных функций с нонарным результатом (выходом).
Троичный дешифратор «2 трита в 9 строк»
Результат изменяется при перемене мест операндов.
Можно рассматривать как объединение девяти бинарных троичных функций с унарными результатами.
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 7 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Бинарные троичные логические функции с m-арными результатами (выходами)
Всего возможно бинарных троичных функций с m-арным выходом, то есть бесконечное число.
К этим функциям относятся бинарные (двухразрядные) дешифраторы и демультиплексоры с m-арными (m-разрядными) выходами.
Тринарные троичные логические функции (операции, элементы)
Всего возможно простейших тринарных (триарных) троичных функций с m-арным выходом. Из этого числа наибольшую значимость имеют такие тринарные троичные функции, имеющие собственные названия, как тринарные (трёхвходовые, трёхаргументные, трёхоперандные) сборки, полные (трёхаргументные, трёхоперандные) сумматоры, шифраторы, дешифраторы, мультиплексоры, демультиплексоры.
Тринарные троичные логические функции (операции) с унарным выходом
Всего возможно (7 триллионов 625 миллиардов 597 миллионов 484 тысячи 987) простейших тринарных (триарных) троичных функций с унарным выходом.
Минимум
Вычисляется min(x, y, z)
27 входных комтринаций
Результат не изменяется при перемене мест операндов.
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-й аргумент (операнд) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-й аргумент (операнд) | ||
| x2=z | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3-й аргумент (операнд) | ||
| FT3N6 056 723 349 50410 | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | результат min(x,y,z) |
Максимум
Вычисляется max(x, y, z)
27 входных комтринаций
Результат не изменяется при перемене мест операндов.
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-й аргумент (операнд) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-й аргумент (операнд) | ||
| x2=z | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3-й аргумент (операнд) | ||
| FT3N7 625 595 420 67210 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 0 | результат max(x,y,z) |
Равенство
Вычисляется равенство всех трёх операндов x=y=z; eq20(x, y, z)
Результат не изменяется при перемене мест операндов.
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-й аргумент (операнд) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-й аргумент (операнд) | ||
| x2=z | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3-й аргумент (операнд) | ||
| FT3N5 083 734 999 04010 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | результат eq20(x,y,z) |
Бинарный мультиплексор «2 в 1» с выключением
При z=0 пропускает на выход только первый аргумент,
при z=1 пропускает на выход только второй аргумент,
при z=2 выключается и ничего не пропускает на выход.
В троичной несимметричной системе кодирования с обозначением (-1,0,+1)=(0,1,2).
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-й аргумент (операнд) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-й аргумент (операнд) | ||
| x2=z | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3-й аргумент (операнд) управляющий | ||
| FT3N379 996 22410 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | результат MUX(x,y,z) |
Бинарный мультиплексор «2 в 1»
Смешанная троично-двоичная функция, два аргумента которой x и y — троичные, а третий z — двоичный.
При z=0 пропускает на выход только первый аргумент,
при z=1 пропускает на выход только второй аргумент.
В троичной несимметричной системе кодирования с обозначением (-1,0,+1)=(0,1,2).
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-й аргумент (операнд) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-й аргумент (операнд) | |
| x2=z | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3-й аргумент (операнд) управляющий | |
| FT2B1N379 996 22410 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | результат MUX(x,y,z) |
Функция имеет тот же номер, что и предыдущая, но 3-й аргумент двоичный, а не троичный. T2 обозначает, что два аргумента троичные несимметричные, а B1 (Binary) обозначает, что один аргумент двоичный.
Единица переноса при полном троичном сложении в несимметричной троичной системе счисления
Функция смешанная, троично-двоичная. Два аргумента x и y — троичные, а третий аргумент z — двоичный.
Результат не изменяется при перемене мест операндов.
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е слагаемое |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е слагаемое |
| x2=z | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Перенос из (n − 1)-го разряда |
| FT2B1N193 099 21610 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | Перенос в (n + 1)-й разряд |
Функция со всеми тремя троичными аргументами, имеет такой же номер, но T2 обозначает, что два аргумента троичные несимметричные, а 1B (Binary) обозначает, что один аргумент двоичный.
Сумма по модулю 3 при полном троичном сложении в несимметричной троичной системе счисления
Полное троичное сложение — тринарная (трёхаргументная, трёхоперандная) троичная функция учитывающая единицу переноса из предыдущего разряда.
Функция смешанная, троично-двоичная. Два аргумента x и y — троичные, а третий аргумент z — двоичный.
Результат не изменяется при перемене мест операндов.
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е слагаемое |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е слагаемое |
| x2=z | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Перенос из (n − 1)-го разряда |
| FT2B1N30731891210 | 2 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 1 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | Сумма по модулю 3 |
Функция со всеми тремя троичными аргументами, имеет такой же номер, но T2 обозначает, что два аргумента троичные несимметричные, а B1 (Binary) обозначает, что один аргумент двоичный.
Тринарные троичные логические функции (операции, элементы) с бинарным (двухразрядным) результатом (выходом)
Всего возможно (58 септиллионов 149 секстиллионов 737 квинтиллионов 003 квадриллиона 040 триллионов 059 миллиардов 690 миллионов 390 тысяч 169) простейших тринарных (триарных) троичных функций с бинарным выходом. Из этого числа наибольшую значимость имеют такие тринарные троичные функции, имеющие собственные названия, как сумматоры, шифраторы, дешифраторы, мультиплексоры, демультиплексоры.
Полное троичное несимметричное сложение в несимметричной троичной системе счисления
Полный одноразрядный троичный несимметричный сумматор является тринарной троичной логической функцией. Разряд (трит) переноса имеет только два значения 0 и 1 из трёх возможных. В отличие от предыдущих троичных тринарных функций с одноразрядным результатом, результат имеет длину 1 и 2/3 троичных разряда.
Результат не изменяется при перемене мест операндов.
| x0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1-е слагаемое |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2-е слагаемое |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Перенос из (n − 1)-го разряда |
| FT2B1N307 318 91210 | 2 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 1 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | МЗР (трит) несимметричной суммы, сумма по модулю 3 |
| FT2B1N193 099 21610 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | СЗР (бит) несимметричной суммы, бит переноса в (n + 1)-й разряд |

В разряде переноса не бывает третьего значения троичного разряда (2), так как в «худшем» случае , то есть в старшем разряде «1». Единица переноса возникает в 9 случаях из 18.
Как в двоичной логике двоичный тринарный полный сумматор заменяется двумя бинарными полусумматорами, так и в троичной логике троичный тринарный полный сумматор можно заменить на два троичных бинарных полусумматора, только с той разницей, что два двоичных бинарных полусумматора одинаковые, а два троичных бинарных полусумматора разные.
1. Один полусумматор полный бинарный («сложение двух полных троичных разрядов»). Второй полусумматор — не полный бинарный («сложение одного полного троичного разряда с неполным троичным разрядом (с 2/3 от полного троичного разряда)»), так как в разряде переноса не бывает значений больших чем «1».
2. Один неполный бинарный «сложение 1 троичного разряда с 2/3 троичного разряда». Второй бинарный несимметричный «сложение 1 троичного разряда с 1 и 2/3 троичного разряда». Результат — двухразрядный длиной 1 и 2/3 троичных разряда.
Полное троичное логическое вычитание с займом в несимметричной троичной системе счисления
Полный троичный одноразрядный вычитатель является неполной тринарной троичной логической функцией, так как в разряде займа только два значения 0 и 1. Результат имеет длину 1 и 2/3 троичных разряда.
Результат изменяется при перемене мест операндов.
| x0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | уменьшаемое |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 1-е вычитаемое |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2-е вычитаемое, заём в (n − 1)-й разряд |
| FT2B1N305 269 05610 | 2 | 1 | 0 | 0 | 2 | 1 | 1 | 0 | 2 | 0 | 2 | 1 | 1 | 0 | 2 | 2 | 1 | 0 | МЗР разности, разность по модулю 3 |
| FT2B1N188 684 17610 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | СЗР разности, заём из (n + 1)-го разряда |
В разряде займа не бывает третьего значения троичного разряда (2), так как в «худшем» случае , то есть в старшем разряде «1». Единица займа возникает в 9 случаях из 18.
Троичный симметричный сумматор-вычитатель
В отличие от несимметричной троичной системы счисления, в которой сумматор и вычитатель являются разными устройствами, в троичной симметричной системе счисления (Фибоначчи) сложение и вычитание выполняются одним устройством — троичным симметричным сумматором-вычитателем, состоящим из двух троичных функций.
Троичный симметричный сумматор-вычитатель
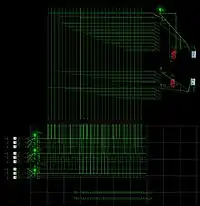
В отличие от сложения в несимметричной троичной системе счисления при сложении в симметричной троичной системе счисления в разряде переноса могут быть все три значения (-1,0,1), поэтому число комтринаций увеличивается с 18 до 27.
Результат не изменяется при перемене мест операндов.
В троичной симметричной системе счисления со знаками (i,0,1)=(-1,0,+1).
В виде таблицы истинности:
| x0=x | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | 1 | 0 | i | Обозначение | 1-е слагаемое | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 1 | 1 | 1 | 0 | 0 | 0 | i | i | i | 1 | 1 | 1 | 0 | 0 | 0 | i | i | i | 1 | 1 | 1 | 0 | 0 | 0 | i | i | i | 2-е слагаемое | |||
| x2=z | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | i | i | i | i | i | i | i | i | i | Перенос из (n − 1)-го разряда | |||
| 0 | i | 1 | i | 1 | 0 | 1 | 0 | i | i | 1 | 0 | 1 | 0 | i | 0 | i | 1 | 1 | 0 | i | 0 | i | 1 | i | 1 | 0 | FT3S-62460370377610(x,y,z) | МЗР (мл. знач. разр.) суммы | |||
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | i | 0 | 0 | 0 | 0 | 0 | i | 0 | i | i | FT3S348342673704810(x,y,z) | СЗР суммы, перенос в n+1 |
перенос (1 или −1) возникает в 8 случаях из 27, четыре раза −1 и четыре раза 1.
В троичной симметричной системе счисления со знаками (2,0,1)=(-1,0,+1).
В виде двух кубов размером 3x3x3 (типа кубика Рубика):
Куба младшего разряда суммы, состоящего из трёх слоёв:
y z = 0 y z = 1 y z = 2
^ ^ ^
| | |
2 0 1 0 1 2 1 2 0
- 1 2 0 -> x - 2 0 1 -> x - 0 1 2 -> x
0 1 2 1 2 0 2 0 1
| | |
FT2N8229 FT2N15613 FT2N5681
и куба старшего разряда суммы (переноса), состоящего из трёх слоёв:
y z = 0 y z = 1 y z = 2
^ ^ ^
| | |
0 0 2 0 0 0 2 0 2
- 0 1 0 -> x - 1 1 0 -> x - 0 0 0 -> x
0 0 0 0 1 0 0 0 2
| | |
FT2N13203 FT2N111 FT2N14598
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | A, 1-е слагаемое | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | B, 2-е слагаемое | ||
| x2=z | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Cin, перенос из (n − 1)-го разряда | ||
| FT3N220124309094410 | 0 | 2 | 1 | 2 | 1 | 0 | 1 | 0 | 2 | 2 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 1 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | S, МЗР (мл. знач. разр.) суммы | ||
| FT3N565556647361510 | 2 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | Cout, СЗР суммы, перенос в n+1 |
В виде двух строк:
строки значений младшего разряда (трита) S суммы:
021210102210102021102021210 или c зада наперёд 012120201120201012201012120
строки значений старшего разряда (трита) Cout суммы (трита переноса):
202000200000011010200010000 или с зада наперёд 000010002010110000002000202
Одна из множества возможных реализаций табличного троичного симметричного сумматора:
на Java:
// Табличный одноразрядный (однотритный) троичный симметричный сумматор-вычитатель
// в системе обозначений (-1,0,+1)=(2,0,1)
import java.io.*;
class TernaryAdderSubstractor
{
public static void main (String[] args) throws java.lang.Exception
{
int[][][]S={{{0,1,2},{1,2,0},{2,0,1}},{{1,2,0},{2,0,1},{0,1,2}},{{2,0,1},{0,1,2},{1,2,0}}};
int[][][]C={{{0,0,0},{0,1,0},{0,0,2}},{{0,1,0},{1,1,0},{0,0,0}},{{0,0,2},{0,0,0},{2,0,2}}};
int A = 2; // (2,0,1)=(-1,0,+1)
int B = 2; // (2,0,1)=(-1,0,+1)
int Cin=2; // (2,0,1)=(-1,0,+1)
System.out.println("" + C[A][B][Cin] + S[A][B][Cin]);
}
}
на JavaScript:
// Табличный одноразрядный (однотритный) троичный симметричный сумматор-вычитатель
// в системе обозначений (-1,0,+1)=(2,0,1)
//importPackage(java.io);
importPackage(java.lang);
var S=[[[0,1,2],[1,2,0],[2,0,1]],[[1,2,0],[2,0,1],[0,1,2]],[[2,0,1],[0,1,2],[1,2,0]]];
var C=[[[0,0,0],[0,1,0],[0,0,2]],[[0,1,0],[1,1,0],[0,0,0]],[[0,0,2],[0,0,0],[2,0,2]]];
var A = 2; // (2,0,1)=(-1,0,+1)
var B = 2; // (2,0,1)=(-1,0,+1)
var Cin=2; // (2,0,1)=(-1,0,+1)
System.out.println( C[A][B][Cin].toString() + S[A][B][Cin].toString() );
//alert( C[A][B][Cin].toString() + S[A][B][Cin].toString() ); // For Plunker (plnkr.co/edit)
на Python:
"""Табличный одноразрядный (однотритный) троичный симметричный сумматор-вычитатель
в системе обозначений (-1,0,+1)=(2,0,1)"""
S = [[[0,1,2],[1,2,0],[2,0,1]],[[1,2,0],[2,0,1],[0,1,2]],[[2,0,1],[0,1,2],[1,2,0]]]
C = [[[0,0,0],[0,1,0],[0,0,2]],[[0,1,0],[1,1,0],[0,0,0]],[[0,0,2],[0,0,0],[2,0,2]]]
A = 2
B = 2
Cin=2
print C[A][B][Cin],S[A][B][Cin]
на С++:
// Табличный одноразрядный (однотритный) троичный симметричный сумматор-вычитатель
// в системе обозначений (-1,0,+1)=(2,0,1)
#include <iostream>
using namespace std;
void main() {
int S[3][3][3]={0,1,2,1,2,0,2,0,1, 1,2,0,2,0,1,0,1,2, 2,0,1,0,1,2,1,2,0};
int C[3][3][3]={0,0,0,0,1,0,0,0,2, 0,1,0,1,1,0,0,0,0, 0,0,2,0,0,0,2,0,2};
int A = 2; // (2,0,1)=(-1,0,+1)
int B = 2; // (2,0,1)=(-1,0,+1)
int Cin=0; // (2,0,1)=(-1,0,+1)
cout << C[A][B][Cin] << ' ' << S[A][B][Cin];
}
на C:
// Табличный одноразрядный (однотритный) троичный симметричный сумматор-вычитатель
// в системе обозначений (-1,0,+1)=(2,0,1)
#include <stdio.h>
void main() {
int S[3][3][3]={0,1,2,1,2,0,2,0,1, 1,2,0,2,0,1,0,1,2, 2,0,1,0,1,2,1,2,0};
int C[3][3][3]={0,0,0,0,1,0,0,0,2, 0,1,0,1,1,0,0,0,0, 0,0,2,0,0,0,2,0,2};
int A = 2; // (2,0,1)=(-1,0,+1)
int B = 2; // (2,0,1)=(-1,0,+1)
int Cin=2; // (2,0,1)=(-1,0,+1)
printf("%i%i", C[A][B][Cin], S[A][B][Cin]);
}
на PHP:
<?php
// Табличный одноразрядный (однотритный) троичный симметричный сумматор-вычитатель
// в системе обозначений (-1,0,+1)=(2,0,1)
$S=[[[0,1,2],[1,2,0],[2,0,1]],[[1,2,0],[2,0,1],[0,1,2]],[[2,0,1],[0,1,2],[1,2,0]]];
$C=[[[0,0,0],[0,1,0],[0,0,2]],[[0,1,0],[1,1,0],[0,0,0]],[[0,0,2],[0,0,0],[2,0,2]]];
$A = 2;
$B = 2;
$Cin=2;
echo(int)($C[$A][$B][$Cin]);
echo(int)($S[$A][$B][$Cin]);
?>
(Проверить и изменить коды программ на Java, JavaScript, Python, C++, C, PHP и др. можно во многих онлайн компиляторах, например в онлайн компиляторе для 60 языков программирования на сайте ideone.com[34].)
на TB:
' Save this supermain program as file "job.bas"
$include "main%.bas"
if fn main% then print "Job done. No errors."
end
' Save this main program (function main%) as file "main%.bas"
' One trit ternary simmetric adder-subtractor
' in simbol sistem (-1,0,+1)=(2,0,1)
$include "tlib.inc"
def fn main%
dim S%(2,2,2):data 0,1,2,1,2,0,2,0,1, 1,2,0,2,0,1,0,1,2, 2,0,1,0,1,2,1,2,0:_call it3df(S%())
dim C%(2,2,2):data 0,0,0,0,1,0,0,0,2, 0,1,0,1,1,0,0,0,0, 0,0,2,0,0,0,2,0,2:_call it3df(C%())
A% = 2 ' (2,0,1)=(-1,0,+1)
B% = 2 ' (2,0,1)=(-1,0,+1)
Cin%=0 ' (2,0,1)=(-1,0,+1)
print C%(A%,B%,Cin%) ; " " ; S%(A%,B%,Cin%)
fn main% = -1
end def
' Save this sub in file "tlib.inc"
sub it3df (F%(3)) ' InitTernary3DimentionFunction F%()
local i%,j%,k%
for i%=0 to 2
for j%=0 to 2
for k%=0 to 2
read F% (i%,j%,k%)
next k%
next j%
next i%
end sub
В троичной симметричной системе счисления со знаками (0,1,2)=(-1,0,+1).
В виде двух кубов размером 3x3x3 (типа кубика Рубика):
Куба младшего разряда суммы, состоящего из трёх слоёв:
y z = 0 y z = 1 y z = 2
^ ^ ^
| | |
0 1 2 1 2 0 2 0 1
- 2 0 1 -> x - 0 1 2 -> x - 1 2 0 -> x
1 2 0 2 0 1 0 1 2
| | |
FT2N15613 FT2N5681 FT2N8229
и куба старшего разряда суммы (переноса), состоящего из трёх слоёв:
y z = 0 y z = 1 y z = 2
^ ^ ^
| | |
1 1 1 1 1 2 1 2 2
- 0 1 1 -> x - 1 1 1 -> x - 1 1 2 -> x
0 0 1 0 1 1 1 1 1
| | |
FT2N9810 FT2N16401 FT2N18832
В виде таблицы истинности:
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | A, 1-е слагаемое | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | B, 2-е слагаемое | ||
| x2=z | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Cin, перенос из (n − 1)-го разряда | ||
| FT3N3 188 195 065 85610 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | 0 | 2 | 1 | 2 | 1 | 0 | 1 | 0 | 2 | 2 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 1 | S, МЗР (мл. знач. разр.) суммы | ||
| FT3N7 296 225 640 44810 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | Cout, СЗР суммы, перенос в n+1 |
ноль в разряде переноса возникает в 4 случаях, единица в разряде переноса возникает в 18 случаях, двойка в разряде переноса возникает в 4 случаях.
В виде двух строк:
строки значений младшего разряда (трита) S суммы:
102021210021210102210102021 или c зада наперёд 120201012201012120012120201
строки значений старшего разряда (трита) Cout суммы (трита переноса):
221211111211111110111110100 или с зада наперёд 001011111011111112111112122
Тринарные троичные функции с тринарным выходом
Всего возможны ≈4.43*1038 простейших тринарных троичных функций с тринарным выходом.
Троичный дешифратор «2 и 2/3 трита в 18 строк»
Можно рассматривать как объединение 18 тринарных (триарных) троичных функций с унарными результатами (выходами).
Результат не изменяется при перемене мест операндов.
| x0=x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1=y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| x2=z | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 16 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Троичный дешифратор «3 трита в 27 строк»
Можно рассматривать как объединение 27 тринарных (триарных) троичных функций с унарными результатами (выходами).
Тетрарные троичные логические функции (операции, элементы) с m-арным результатом
Всего возможно простейших тетрарных троичных функций с m-арным выходом.
Тетрарные троичные логические функции (операции, элементы) с унарным результатом
Всего возможно простейших тетрарных троичных функций с унарным выходом.
Троичный тринарный (трёхвходовой) мультиплексор
Имеет четыре входа:
1. первое троичное число
2. второе троичное число
3. третье троичное число
4. троичный сигнал переключения 3 входов
и один выход:
1. выбранное троичное число
В троичном несимметричном кодировании с обозначениями (−1, 0, +1) = (0, 1, 2):
Таблица истинности:
| x0=x | x | x | x | 1-й аргумент (операнд) |
|---|---|---|---|---|
| x1=y | y | y | y | 2-й аргумент (операнд) |
| x2=z | z | z | z | 3-й аргумент (операнд) |
| x3=u | 2 | 1 | 0 | 4-й аргумент (операнд) управляющий |
| FT4NMUX(x,y,z,u) | z | y | x | результат действия тетрарной троичной функции MUX(x,y,z,u) |
Одна из возможных реализаций троичного тринарного мультиплексора, который является тетрарной троичной функцией, средствами только троичных функций и троичных операторов:
- FT4NMUX(x, y,z, u) = FT2N21(x, u) FT2N19569 FT2N567(y, u) FT2N19569 FT2N15309(z, u) =
- = FT2N21(x, u) FT2Nmax FT2N567(y, u) FT2Nmax FT2N15309(z, u) =
- = FT2Nmax(FT2Nmax(FT2N21(x, y),FT2N567(y, x)),FT2N15309(z, u))
Здесь бинарные (двухаргументные) троичные функции FT2N21(x, u), FT2N567(y, u) и FT2N15309(z, u) используются в префиксной записи для выделения первого, второго или третьего операнда, а бинарная (двухоперандная) троичная функция FT2N19569 (FT2Nmax) в первой и второй строке используется в качестве бинарного (двухоперандного) оператора с инфиксной записью в строке, а в третьей строке в качестве бинарной (двухаргументной) троичной функции с префиксной записью в строке для обработки трёх предыдущих результатов, подобно двоичному оператору и функции OR2 (2ИЛИ) в двоичной логике. При этом функции в первой и во второй строке имеют более высший приоритет в строке, то есть выполняются по очереди первыми, а операторы в первой и второй строке имеют более низший приоритет, чем бинарные (двухаргументные) функции, то есть выполняются по очереди вторыми после выполнения функций. Третья строка состоит только из вложенных функций, поэтому функции выполняются по очереди начиная с функции с самым глубоким вложением.
N-арные троичные логические функции
N-арные троичные логические функции
Всего возможно простейших n-арных троичных функций.
К этим функциям относятся n-арные шифраторы и n-арные мультиплексоры.
Примечания
- Троичные триггеры в трёхбитной системе троичных логических элементов 3B BCT (3-Bit BinaryCodedTrinary, «трёхпроводная»)
- Троичные триггеры в трёхуровневой системе троичных логических элементов 3L CT (3-Level CodedTrinary, «однопроводная»)
- Депман И. Я. Возникновение системы мер и способов измерения величин. Выпуск 1. (1956) Глава VIII. Задача Д. И. Менделеева о наилучшей системе гирь. § Все числа троичной системы могут быть записаны при помощи двух цифр: 0 или 1. С. 113.
- Unary Operations. Table 4: Rotate Up https://web.archive.org/web/20080622120236/http://www.trinary.cc/Tutorial/Algebra/Unary.htm
- http://jeff.tk:81/wiki/Trinary/Logic Архивная копия от 12 мая 2010 на Wayback Machine A.3.1. Constant Functions. Table A.3. Constant Functions и A.3.2. One-to-one Functions. Table A.4. One-to-one Functions
- Unary Operations. Table 7: Shift Down https://web.archive.org/web/20080622120236/http://www.trinary.cc/Tutorial/Algebra/Unary.htm
- Unary Operations. Table 5: Rotate Down https://web.archive.org/web/20080622120236/http://www.trinary.cc/Tutorial/Algebra/Unary.htm
- Unary Operations. Table 6: Shift Up https://web.archive.org/web/20080622120236/http://www.trinary.cc/Tutorial/Algebra/Unary.htm
- http://andserkul.narod2.ru/troichnie_alu/ А. С. Куликов. Троичные АЛУ
- https://web.archive.org/web/20080611055612/http://www.trinary.cc/ Веб архив. Сайт Стива Грабба Trinary.cc
- Материалы по троичной информатике. Аппаратная реализация. Маслов С. П. Троичная схемотехника
- Unary Operations. Invert https://web.archive.org/web/20080622120236/http://www.trinary.cc/Tutorial/Algebra/Unary.htm
- Circuits. Logic Families. Ternary. Complement(F210)
- Circuits. Logic Families. Ternary. F220
- Circuits. Logic Families. Ternary. F211
- Circuits. Logic Families. Ternary. F221
- http://jeff.tk:81/wiki/Trinary/Logic Архивная копия от 12 мая 2010 на Wayback Machine A.3.2. One-to-one Functions. Table A.4. One-to-one Functions
- Троичные трёхбитные триггеры
- Circuit. Logic Families. Ternary. CGOR
- Binary Function. Table 11: The Mean Function https://web.archive.org/web/20080623205822/http://www.trinary.cc/Tutorial/Algebra/Binary.htm
- Binary Functions. Mean https://web.archive.org/web/20080623205822/http://www.trinary.cc/Tutorial/Algebra/Binary.htm
- Circuit. Logic Families. Ternary. CGAND
- Binary Functions. Table 12: The Magnitude Function https://web.archive.org/web/20080623205822/http://www.trinary.cc/Tutorial/Algebra/Binary.htm
- [Binary Operations. Table 8: The Min Function (A↓B) https://web.archive.org/web/20080623205822/http://www.trinary.cc/Tutorial/Algebra/Binary.htm]
- [Binary Operations. Min https://web.archive.org/web/20080623205822/http://www.trinary.cc/Tutorial/Algebra/Binary.htm]
- [Binary Operations. Table 9: The Max Function (A↑B) https://web.archive.org/web/20080623205822/http://www.trinary.cc/Tutorial/Algebra/Binary.htm]
- [Binary Operations. Max https://web.archive.org/web/20080623205822/http://www.trinary.cc/Tutorial/Algebra/Binary.htm]
- Анатолий Медынцев. Обратимая троичная операция (недоступная ссылка). Дата обращения: 6 февраля 2012. Архивировано 25 июня 2012 года.
- http://www.pcmag.ru/solutions/sub_detail.php?ID=1985&SUB_PAGE=4 Суждение и вычисление: не исключая третье. Александр Рябцев. Импликация Лукасевича
- http://society.polbu.ru/tvardovsky_lvovwarsawphilo/ch43_i.html Архивная копия от 15 июля 2014 на Wayback Machine К. Твардовский. Львовско-Варшавская философская школа. Исторические исследования логики Я.Лукасевичем
- Three Valued Logic. 4. Сведения по трёхзначной логике
- http://www.inp.nsk.su/~kozak/ttl/ttlh01.htm Справочник по стандартным цифровым ТТЛ микросхемам
- http://andserkul.narod2.ru/troichnie_summatori/ А. С. Куликов. Троичные сумматоры
- Онлайн компилятор для 60 языков программирования
Литература
- D. C. Rine (ed.), Computer Science and Multiple-Valued Logic. Theory and Applications. Elsevier, 1977, 548p. ISBN 978-0-7204-0406-7