Сортировка слиянием
Сортировка слиянием (англ. merge sort) — алгоритм сортировки, который упорядочивает списки (или другие структуры данных, доступ к элементам которых можно получать только последовательно, например — потоки) в определённом порядке. Эта сортировка — хороший пример использования принципа «разделяй и властвуй». Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Наконец, их решения комбинируются, и получается решение исходной задачи.
| Сортировка слиянием | |
|---|---|
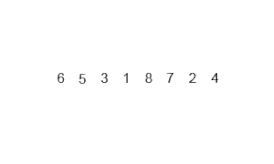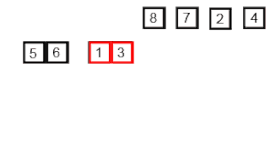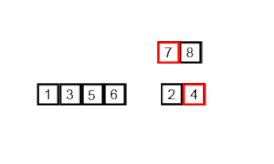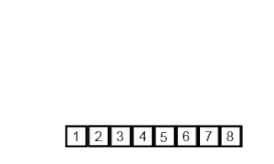 Пример сортировки слиянием. Сначала делим список на кусочки (по 1 элементу), затем сравниваем каждый элемент с соседним, сортируем и объединяем. В итоге, все элементы отсортированы и объединены вместе. | |
| Автор | Джон фон Нейман |
| Предназначение | Алгоритм сортировки |
| Структура данных | список, массив |
| Худшее время | |
| Лучшее время | |
| Среднее время | |
| Затраты памяти | для списка, для массива |
Подробный алгоритм сортировки

Для решения задачи сортировки эти три этапа выглядят так:
- Сортируемый массив разбивается на две части примерно одинакового размера;
- Каждая из получившихся частей сортируется отдельно, например — тем же самым алгоритмом;
- Два упорядоченных массива половинного размера соединяются в один.
1.1. — 2.1. Рекурсивное разбиение задачи на меньшие происходит до тех пор, пока размер массива не достигнет единицы (любой массив длины 1 можно считать упорядоченным).
3.1. Соединение двух упорядоченных массивов в один.
Основную идею слияния двух отсортированных массивов можно объяснить на следующем примере. Пусть мы имеем два уже отсортированных по возрастанию подмассива. Тогда:
3.2. Слияние двух подмассивов в третий результирующий массив.
На каждом шаге мы берём меньший из двух первых элементов подмассивов и записываем его в результирующий массив. Счётчики номеров элементов результирующего массива и подмассива, из которого был взят элемент, увеличиваем на 1.
3.3. «Прицепление» остатка.
Когда один из подмассивов закончился, мы добавляем все оставшиеся элементы второго подмассива в результирующий массив.
Пример сортировки на языке С
/**
* Сортирует массив, используя рекурсивную сортировку слиянием
* up - указатель на массив, который нужно сортировать
* down - указатель на массив с, как минимум, таким же размером как у 'up', используется как буфер
* left - левая граница массива, передайте 0, чтобы сортировать массив с начала
* right - правая граница массива, передайте длину массива - 1, чтобы сортировать массив до последнего элемента
* возвращает: указатель на отсортированный массив. Из-за особенностей работы данной реализации
* отсортированная версия массива может оказаться либо в 'up', либо в 'down'
**/
int* merge_sort(int *up, int *down, unsigned int left, unsigned int right)
{
if (left == right)
{
down[left] = up[left];
return down;
}
unsigned int middle = left + (right - left) / 2;
// разделяй и сортируй
int *l_buff = merge_sort(up, down, left, middle);
int *r_buff = merge_sort(up, down, middle + 1, right);
// слияние двух отсортированных половин
int *target = l_buff == up ? down : up;
unsigned int l_cur = left, r_cur = middle + 1;
for (unsigned int i = left; i <= right; i++)
{
if (l_cur <= middle && r_cur <= right)
{
if (l_buff[l_cur] < r_buff[r_cur])
{
target[i] = l_buff[l_cur];
l_cur++;
}
else
{
target[i] = r_buff[r_cur];
r_cur++;
}
}
else if (l_cur <= middle)
{
target[i] = l_buff[l_cur];
l_cur++;
}
else
{
target[i] = r_buff[r_cur];
r_cur++;
}
}
return target;
}
Реализация на языке C++11:
#include <algorithm>
#include <cstddef>
#include <iterator>
#include <memory>
template<typename T>
void merge_sort(T array[], std::size_t size) noexcept
{
if (size > 1)
{
std::size_t const left_size = size / 2;
std::size_t const right_size = size - left_size;
merge_sort(&array[0], left_size);
merge_sort(&array[left_size], right_size);
std::size_t lidx = 0, ridx = left_size, idx = 0;
std::unique_ptr<T[]> tmp_array(new T[size]);
while (lidx < left_size || ridx < size)
{
if (array[lidx] < array[ridx])
{
tmp_array[idx++] = std::move(array[lidx]);
lidx++;
}
else
{
tmp_array[idx++] = std::move(array[ridx]);
ridx++;
}
if (lidx == left_size)
{
std::copy(std::make_move_iterator(&array[ridx]),
std::make_move_iterator(&array[size]),
&tmp_array[idx]);
break;
}
if (ridx == size)
{
std::copy(std::make_move_iterator(&array[lidx]),
std::make_move_iterator(&array[left_size]),
&tmp_array[idx]);
break;
}
}
std::copy(std::make_move_iterator(tmp_array),
std::make_move_iterator(&tmp_array[size]),
array);
}
}
Реализация на языке С++14 с распараллеливанием от OpenMP
#include <algorithm>
#include <iterator>
#include <omp.h>
#include <memory>
template <typename Iterator>
void mergesort(Iterator from, Iterator to)
{
#pragma omp parallel
{
#pragma omp single nowait
static_assert(!std::is_same<typename std::iterator_traits<Iterator>::value_type, void>::value);
auto n = std::distance(from, to);
if (1 < n)
{
#pragma omp task firstprivate (from, to, n)
{
Iterator l_from = from;
Iterator l_to = l_from;
std::advance(l_to, n/2);
mergesort(l_from, l_to);
}
#pragma omp task firstprivate (from, to, n)
{
Iterator r_from = from;
std::advance(r_from, n/2);
Iterator r_to = r_from;
std::advance(r_to, n-(n/2));
mergesort(r_from, r_to);
}
#pragma omp taskwait
auto tmp_array = std::make_unique<typename Iterator::value_type[]>(n);
Iterator l_iter = from;
Iterator l_end = l_iter;
std::advance(l_end, n/2);
Iterator r_iter = l_end;
Iterator& r_end = to;
auto tmp_iter = tmp_array.get();
while (l_iter != l_end || r_iter != r_end)
{
if (*l_iter < *r_iter)
{
*tmp_iter = std::move(*l_iter);
++l_iter;
++tmp_iter;
}
else
{
*tmp_iter = std::move(*r_iter);
++r_iter;
++tmp_iter;
}
if (l_iter == l_end)
{
std::copy(
std::make_move_iterator(r_iter),
std::make_move_iterator(r_end),
tmp_iter
);
break;
}
if (r_iter == r_end)
{
std::copy(
std::make_move_iterator(l_iter),
std::make_move_iterator(l_end),
tmp_iter
);
break;
}
}
std::copy(
std::make_move_iterator(tmp_array.get()),
std::make_move_iterator(&tmp_array[n]),
from
);
}
}
}
Итеративная реализация на языке C++:
template<typename T>
void MergeSort(T a[], size_t l)
{
size_t BlockSizeIterator;
size_t BlockIterator;
size_t LeftBlockIterator;
size_t RightBlockIterator;
size_t MergeIterator;
size_t LeftBorder;
size_t MidBorder;
size_t RightBorder;
for (BlockSizeIterator = 1; BlockSizeIterator < l; BlockSizeIterator *= 2)
{
for (BlockIterator = 0; BlockIterator < l - BlockSizeIterator; BlockIterator += 2 * BlockSizeIterator)
{
//Производим слияние с сортировкой пары блоков начинающуюся с элемента BlockIterator
//левый размером BlockSizeIterator, правый размером BlockSizeIterator или меньше
LeftBlockIterator = 0;
RightBlockIterator = 0;
LeftBorder = BlockIterator;
MidBorder = BlockIterator + BlockSizeIterator;
RightBorder = BlockIterator + 2 * BlockSizeIterator;
RightBorder = (RightBorder < l) ? RightBorder : l;
int* SortedBlock = new int[RightBorder - LeftBorder];
//Пока в обоих массивах есть элементы выбираем меньший из них и заносим в отсортированный блок
while (LeftBorder + LeftBlockIterator < MidBorder && MidBorder + RightBlockIterator < RightBorder)
{
if (a[LeftBorder + LeftBlockIterator] < a[MidBorder + RightBlockIterator])
{
SortedBlock[LeftBlockIterator + RightBlockIterator] = a[LeftBorder + LeftBlockIterator];
LeftBlockIterator += 1;
}
else
{
SortedBlock[LeftBlockIterator + RightBlockIterator] = a[MidBorder + RightBlockIterator];
RightBlockIterator += 1;
}
}
//После этого заносим оставшиеся элементы из левого или правого блока
while (LeftBorder + LeftBlockIterator < MidBorder)
{
SortedBlock[LeftBlockIterator + RightBlockIterator] = a[LeftBorder + LeftBlockIterator];
LeftBlockIterator += 1;
}
while (MidBorder + RightBlockIterator < RightBorder)
{
SortedBlock[LeftBlockIterator + RightBlockIterator] = a[MidBorder + RightBlockIterator];
RightBlockIterator += 1;
}
for (MergeIterator = 0; MergeIterator < LeftBlockIterator + RightBlockIterator; MergeIterator++)
{
a[LeftBorder + MergeIterator] = SortedBlock[MergeIterator];
}
delete SortedBlock;
}
}
}
Реализация на языке Python:
def merge_sort(A):
if len(A) == 1 or len(A) == 0:
return A
L = merge_sort(A[:len(A) // 2])
R = merge_sort(A[len(A) // 2:])
n = m = k = 0
C = [0] * (len(L) + len(R))
while n < len(L) and m < len(R):
if L[n] <= R[m]:
C[k] = L[n]
n += 1
else:
C[k] = R[m]
m += 1
k += 1
while n < len(L):
C[k] = L[n]
n += 1
k += 1
while m < len(R):
C[k] = R[m]
m += 1
k += 1
for i in range(len(A)):
A[i] = C[i]
return A
Реализация на языке Go:
func mergeSort(list []int) []int {
count := len(list)
switch {
case count > 2:
lb := mergeSort(list[:count/2])
rb := mergeSort(list[count/2:])
list = append(lb, rb...)
lastIndex := len(list) - 1
for i := 0; i < lastIndex; i++ {
mv := list[i]
mi := i
for j := i + 1; j < lastIndex+1; j++ {
if mv > list[j] {
mv = list[j]
mi = j
}
}
if mi != i {
list[i], list[mi] = list[mi], list[i]
}
}
case len(list) > 1 && list[0] > list[1]:
list[0], list[1] = list[1], list[0]
}
return list
}
Псевдокод алгоритма слияния без «прицепления» остатка на C++-подобном языке:
L = *In1;
R = *In2;
if( L == R ) {
*Out++ = L;
In1++;
*Out++ = R;
In2++;
} else if(L < R) {
*Out++ = L;
In1++;
} else {
*Out++ = R;
In2++;
}
Алгоритм был изобретён Джоном фон Нейманом в 1945 году[1].
В приведённом алгоритме на C++-подобном языке используется проверка на равенство двух сравниваемых элементов подмассивов с отдельным блоком обработки в случае равенства. Отдельная проверка на равенство удваивает число сравнений, что усложняет код программы. Вместо отдельной проверки на равенство и отдельного блока обработки в случае равенства можно использовать две проверки if(L <= R) и if(L >= R), что почти вдвое уменьшает код программы.
Псевдокод улучшенного алгоритма слияния без «прицепления» остатка на C++-подобном языке:
L = *In1;
R = *In2;
if( L <= R ) {
*Out++ = L;
In1++;
}
if( L >= R ) {
*Out++ = R;
In2++;
}
Число проверок можно сократить вдвое убрав проверку if(L >= R). При этом, в случае равенства L и R, L запишется в Out в первой итерации, а R - во второй. Этот вариант будет работать эффективно, если в исходном массиве повторяющиеся элементы не будут преобладать над остальными элементами.
Псевдокод сокращенного алгоритма слияния без «прицепления» остатка на C++-подобном языке:
L = *In1;
R = *In2;
if( L <= R ) {
*Out++ = L;
In1++;
} else {
*Out++ = R;
In2++;
}
Две операции пересылки в переменные L и R упрощают некоторые записи в программе, что может оказаться полезным в учебных целях, но в действительных программах их можно удалить, что сократит программный код. Также можно использовать тернарный оператор, что ещё больше сократит программный код.
Псевдокод ещё более улучшенного алгоритма слияния без «прицепления» остатка на C++-подобном языке:
*Out++ = *In1 <= *In2 ? In1++ : In2++;
Время работы алгоритма порядка O(n * log n) при отсутствии деградации на неудачных случаях, которая является больным местом быстрой сортировки (тоже алгоритм порядка O(n * log n), но только для среднего случая). Расход памяти выше, чем для быстрой сортировки, при намного более благоприятном паттерне выделения памяти — возможно выделение одного региона памяти с самого начала и отсутствие выделения при дальнейшем исполнении.
Популярная реализация требует однократно выделяемого временного буфера памяти, равного сортируемому массиву, и не имеет рекурсий. Шаги реализации:
- InputArray = сортируемый массив, OutputArray = временный буфер;
- над каждым отрезком входного массива InputArray[N * MIN_CHUNK_SIZE..(N + 1) * MIN_CHUNK_SIZE] выполняется какой-то вспомогательный алгоритм сортировки, например, сортировка Шелла или быстрая сортировка;
- устанавливается ChunkSize = MIN_CHUNK_SIZE;
- сливаются два отрезка InputArray[N * ChunkSize..(N + 1) * ChunkSize] и InputArray[(N + 1) * ChunkSize..(N + 2) * ChunkSize] попеременным шаганием слева и справа (см. выше), результат помещается в OutputArray[N * ChunkSize..(N + 2) * ChunkSize], и так для всех N, пока не будет достигнут конец массива;
- ChunkSize удваивается;
- если ChunkSize стал >= размера массива, то конец, результат в OutputArray, который (ввиду перестановок, описанных ниже) есть либо сортируемый массив, либо временный буфер, во втором случае он целиком копируется в сортируемый массив;
- иначе меняются местами InputArray и OutputArray перестановкой указателей, и всё повторяется с пункта 4.
Такая реализация также поддерживает размещение сортируемого массива и временного буфера в дисковых файлах, то есть пригодна для сортировки огромных объёмов данных. Реализация ORDER BY в СУБД MySQL при отсутствии подходящего индекса устроена именно так (источник: filesort.cc в исходном коде MySQL).
Пример реализации алгоритма простого двухпутевого слияния на псевдокоде:
function mergesort(m)
var list left, right, result
if length(m) ≤ 1
return m
else
middle = length(m) / 2
for each x in m up to middle
add x to left
for each x in m after middle
add x to right
left = mergesort(left)
right = mergesort(right)
result = merge(left, right)
return result
end if
Есть несколько вариантов функции merge(), наиболее простой вариант может выглядеть так:
function merge(left,right)
var list result
while length(left) > 0 and length(right) > 0
if first(left) ≤ first(right)
append first(left) to result
left = rest(left)
else
append first(right) to result
right = rest(right)
end if
while length(left) > 0
append first(left) to result
left = rest(left)
while length(right) > 0
append first(right) to result
right = rest(right)
return result
Достоинства и недостатки
Достоинства:
- Работает даже на структурах данных последовательного доступа.
- Хорошо сочетается с подкачкой и кэшированием памяти.
- Неплохо работает в параллельном варианте: легко разбить задачи между процессорами поровну, но трудно сделать так, чтобы другие процессоры взяли на себя работу, в случае если один процессор задержится.
- Не имеет «трудных» входных данных.
- Устойчивая - сохраняет порядок равных элементов (принадлежащих одному классу эквивалентности по сравнению).
Недостатки:
- На «почти отсортированных» массивах работает столь же долго, как на хаотичных. Существует вариант сортировки слиянием, который работает быстрее на частично отсортированных данных, но он требует дополнительной памяти, в дополнении ко временному буферу, который используется непосредственно для сортировки.
- Требует дополнительной памяти по размеру исходного массива.
Примечания
- Knuth, D.E. The Art of Computer Programming. Volume 3: Sorting and Searching (англ.). — 2nd. — Addison-Wesley, 1998. — P. 159. — ISBN 0-201-89685-0.
Литература
- Левитин А. В. Глава 4. Метод декомпозиции: Сортировка слиянием // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 169—172. — 576 с. — ISBN 978-5-8459-0987-9
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4.
Ссылки
- Многофазное слияние на algolist.manual.ru
- Сортировка слиянием — восходящая сортировка, естественная сортировка, измерение быстродействия.
- Описание метода и листинг программ сортировки слиянием.
- Динамическая визуализация 7 алгоритмов сортировки с открытым исходным кодом
- Пример реализации на Java