Сортировка выбором
Сортировка выбором (Selection sort) — алгоритм сортировки. Может быть как устойчивый, так и неустойчивый. На массиве из n элементов имеет время выполнения в худшем, среднем и лучшем случае Θ(n2), предполагая что сравнения делаются за постоянное время.
| Сортировка выбором | |
|---|---|
 | |
| Предназначение | Алгоритм сортировки |
| Структура данных | Массив |
| Худшее время | О(n2) |
| Лучшее время | О(n2) |
| Среднее время | О(n2) |
| Затраты памяти | O(1) |
Алгоритм без дополнительного выделения памяти
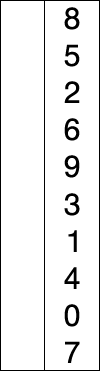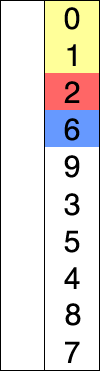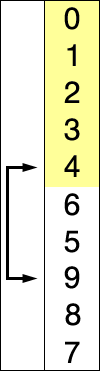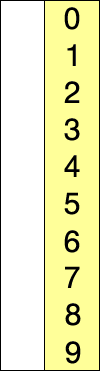
Шаги алгоритма:
- находим номер минимального значения в текущем списке
- производим обмен этого значения со значением первой неотсортированной позиции (обмен не нужен, если минимальный элемент уже находится на данной позиции)
- теперь сортируем хвост списка, исключив из рассмотрения уже отсортированные элементы
Пример неустойчивой реализации:
#include <concepts>
#include <cstddef>
#include <utility>
using namespace std;
template <totally_ordered T, size_t size>
inline void selection_sort(T (&array)[size]) { selection_sort(array, size); }
template <totally_ordered T>
void selection_sort(T array[], size_t size)
{
for (size_t idx_i = 0; idx_i < size - 1; ++idx_i)
{
size_t min_idx = idx_i;
for (size_t idx_j = idx_i + 1; idx_j < size; ++idx_j)
if (array[idx_j] < array[min_idx])
min_idx = idx_j;
if (min_idx != idx_i)
swap(array[idx_i], array[min_idx]);
}
}
public static IList<T> Selection<T>(IList<T> list) where T : IComparable<T>
{
for (int i = 0; i < list.Count - 1; ++i)
{
int min = i;
for (int j = i + 1; j < list.Count; ++j)
{
if (list[j].CompareTo(list[min]) < 0)
{
min = j;
}
}
var dummy = list[i];
list[i] = list[min];
list[min] = dummy;
}
return list;
}
type sort_choice_list is table of integer index by binary_integer;
---------------------------------------------
function SORT_CHOICE return sort_choice_list
IS
list sort_choise_list;
l_min pls_integer;
l_dummy pls_integer;
begin
for n in 1..100 loop
list(n):=dbms_random.random; --инициализация массива случайными числами
end loop;
for i in list.first..list.last loop
l_min:=i;
for j in (i + 1)..list.last loop
if (list(j) < list(l_min)) then
l_min := j;
end if;
end loop;
l_dummy:=list(i);
list(i):=list(l_min);
list(l_min) := l_dummy;
end loop;
return list;
end SORT_CHOICE;
public static <T extends Comparable<? super T>>
void sort(T[] array) {
for (int i = 0; i < array.length - 1; ++i) {
int minPos = i;
for (int j = i + 1; j < array.length; ++j) {
if (array[j].compareTo(array[minPos]) < 0) {
minPos = j;
}
}
T saveValue = array[minPos];
array[minPos] = array[i];
array[i] = saveValue;
}
}
def selection_sort(array)
for min in 0..array.count-2
least = min
for j in (min + 1)..array.count-1
if array[j] < array[least]
least = j
end
end
temp = array[min]
array[min] = array[least]
array[least] = temp
end
end
func selectionSort<Element>(_ array: inout Array<Element>) where Element: Comparable {
for min in 0..<array.count - 1 {
for j in min..<array.count {
if array[j] < array[min] {
let temp = array[min]
array[min] = array[j]
array[j] = temp
}
}
}
}
begin
var a := ArrRandom;
a.Println;
for var i:=0 to a.High do
Swap(a[i],a[i+a[i:].IndexMin]);
a.Println;
end
def select_sort(A):
for i in range(len(A)-1):
for k in range(i+1, len(A)):
if A[k] < A[i]:
A[k], A[i] = A[i], A[k]
func selectionSort(nums []int) {
n := len(nums)
for i := 0; i < n; i++ {
min := i
for j := i + 1; j < n; j++ {
if nums[j] < nums[min] {
min = j
}
}
nums[i], nums[min] = nums[min], nums[i]
}
}
Покажем, почему данная реализация является неустойчивой.
Рассмотрим следующий массив из элементов, каждый из которых имеет два поля. Сортировка идет по первому полю.
Массив до сортировки:
{ (2, a), (2, b), (1, a) }
Уже после первой итерации внешнего цикла будем иметь отсортированную последовательность:
{ (1, a), (2, b), (2, a) }
Теперь заметим, что взаимное расположение элементов (2, a) и (2, b) изменилось. Таким образом, рассматриваемая реализация является неустойчивой.
Так как после каждого прохода по внутреннему циклу делается только один обмен, то общее число обменов равно N-1, что в N/2 раз меньше, чем в сортировке пузырьком.
Число проходов по внутреннему циклу равно N-1 даже в случае сортировки частично или полностью отсортированного массива.
Наихудший случай:
Число сравнений в теле цикла равно (N-1)*N/2.
Число сравнений в заголовках циклов (N-1)*N/2.
Число сравнений перед операцией обмена N-1.
Суммарное число сравнений N2−1.
Число обменов N-1.
Наилучший случай:
Время сортировки 10000 коротких целых чисел на одном и том же программно-аппаратном комплексе сортировкой выбором составило ≈40сек., а ещё более улучшенной сортировкой пузырьком ≈30сек.
Пирамидальная сортировка сильно улучшает базовый алгоритм, используя структуру данных «куча» для ускорения нахождения и удаления минимального элемента.
Существует также двунаправленный вариант сортировки методом выбора, в котором на каждом проходе отыскиваются и устанавливаются на свои места и минимальное, и максимальное значения.
Литература
- Левитин А. В. Глава 3. Метод грубой силы: Сортировка выбором // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 143—144. — 576 с. — ISBN 978-5-8459-0987-9
- Роберт Седжвик. Часть III. Глава 6. Элементарные методы сортировки: 6.2 Сортировка выбором // Алгоритмы на С++ = Algorithms in C++. — М.: «Вильямс», 2011. — С. 246-247. — ISBN 978-5-8459-1650-1.
- Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4.
Ссылки
- Статья "Сортировка выбором" на сайте algolist.manual.ru. Дата обращения: 25 сентября 2012.
- Динамическая визуализация 7 алгоритмов сортировки с открытым исходным кодом