Топологическая сортировка

Для графа ${\displaystyle G={\Bigl (}{\bigl \{}2,3,5,7,8,9,10,11{\bigr \}},{\bigl \{}(3,8),(3,10),(5,11),(7,11),(7,8),(8,9),(11,2),(11,9),(11,10){\bigr \}}{\Bigr )}}$

Бесконтурный ориентированный граф

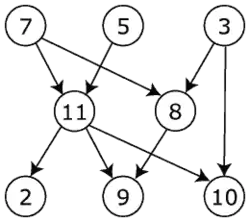
существует несколько согласованных последовательностей его вершин, которые могут быть получены при помощи топологической сортировки, например:

• ${\displaystyle 7,5,11,3,8,2,9,10}$
• ${\displaystyle 3,7,5,8,11,10,9,2}$

Видно, что в последовательности могут быть переставлены любые две стоящие рядом вершины, которые не входят в отношение частичного порядка ${\displaystyle E}$.

Один из первых алгоритмов, и наиболее приспособленный к исполнению вручную.

Пусть дан бесконтурный ориентированный простой граф ${\displaystyle G=(V,E)}$. Через ${\displaystyle A(v),v\in V}$ обозначим множество таких вершин ${\displaystyle u\in V}$, что ${\displaystyle \exists ~(u,v)\in E}$. То есть ${\displaystyle A(v)}$ — множество всех вершин, из которых есть дуга в вершину ${\displaystyle v}$. Пусть ${\displaystyle P}$ — искомая последовательность вершин.

пока ${\displaystyle |P|<|V|}$
  выбрать любую вершину ${\displaystyle v}$ такую, что ${\displaystyle A(v)=\varnothing }$ и ${\displaystyle v\notin P}$
  ${\displaystyle P\gets P,v}$
  удалить ${\displaystyle v}$ из всех ${\displaystyle A(u),u\neq v}$

Наличие хотя бы одного контура в графе приведёт к тому, что на определённой итерации цикла не удастся выбрать новую вершину ${\displaystyle v}$.

Пример работы алгоритма

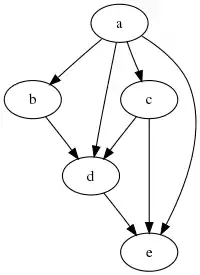
Пусть задан граф ${\displaystyle G={\Bigl (}{\bigl \{}a,b,c,d,e{\bigr \}},{\bigl \{}(a,b),(a,c),(a,d),(a,e),(b,d),(c,d),(c,e),(d,e){\bigr \}}{\Bigr )}}$. В таком случае алгоритм выполнится следующим образом:

шаг	${\displaystyle v}$	${\displaystyle A(a)}$	${\displaystyle A(b)}$	${\displaystyle A(c)}$	${\displaystyle A(d)}$	${\displaystyle A(e)}$	${\displaystyle P}$
0	${\displaystyle -}$	${\displaystyle \varnothing }$	${\displaystyle a}$	${\displaystyle a}$	${\displaystyle a,b,c}$	${\displaystyle a,c,d}$	${\displaystyle \varnothing }$
1	${\displaystyle a}$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle b,c}$	${\displaystyle c,d}$	${\displaystyle a}$
2	${\displaystyle c}$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle b}$	${\displaystyle d}$	${\displaystyle a,c}$
3	${\displaystyle b}$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle d}$	${\displaystyle a,c,b}$
4	${\displaystyle d}$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle a,c,b,d}$
5	${\displaystyle e}$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle \varnothing }$	${\displaystyle a,c,b,d,e}$

На втором шаге вместо ${\displaystyle c}$ может быть выбрана вершина ${\displaystyle b}$, поскольку порядок между ${\displaystyle b}$ и ${\displaystyle c}$ не задан.

На компьютере топологическую сортировку можно выполнить за O(n) времени и памяти, если обойти все вершины, используя поиск в глубину, и выводить вершины в момент выхода из неё.

Другими словами алгоритм состоит в следующем:

• Изначально все вершины белые.
• Для каждой вершины делаем шаг алгоритма.

Шаг алгоритма:

• Если вершина чёрная, ничего делать не надо.
• Если вершина серая — найден цикл, топологическая сортировка невозможна.
• Если вершина белая
  • Красим её в серый
  • Применяем шаг алгоритма для всех вершин, в которые можно попасть из текущей
  • Красим вершину в чёрный и помещаем её в начало окончательного списка.

При помощи топологической сортировки строится корректная последовательность выполнения действий, всякое из которых может зависеть от другого: последовательность прохождения учебных курсов студентами, установки программ при помощи пакетного менеджера, сборки исходных текстов программ при помощи Makefile'ов.

Можно построить список отображения объектов в изометрической проекции зная парные порядковые отношения между объектами (какой из двух объектов должен быть прорисован раньше).

• Алгоритм Демукрона

• Пример алгоритма топологической сортировки на Python, C++, Pascal
• Топологическая сортировка при помощи поиска в глубину — реализация на C++
• Топологическая сортировка на Pascal за O(n + m) от Никлауса Вирта

• Левитин А. В. Глава 5. Метод уменьшения размера задачи: Топологическая сортировка // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 220—224. — 576 с. — ISBN 978-5-8459-0987-9
• Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Глава 22.4. Топологическая сортировка // Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — С. 632-635. — ISBN 5-8459-0857-4.