Символы Кристоффеля
Си́мволы Кристо́ффеля (или кристоффели) — коэффициенты координатного выражения аффинной связности, в частности, связности Леви-Чивиты. Названы в честь Эльвина Бруно Кристоффеля. Используются в дифференциальной геометрии, общей теории относительности и близких к ней теориях гравитации. Появляются в координатном выражении тензора кривизны. При этом сами символы тензорами не являются.
Обычно обозначаются ; иногда, следуя первоначальному обозначению Кристоффеля, используется[1] символ
Ниже используется правило суммирования Эйнштейна, то есть по повторяющимся верхнему и нижнему индексам подразумевается суммирование.
История
Символы впервые появились в статье Кристоффеля «О преобразовании однородных дифференциальных выражений второй степени» (нем. Über die Transformation der homogenen Differentialausdrücke zweiten Grades — J. fur Math., № 70, 1869). В ней автор рассмотрел условия совпадения римановой геометрии, определяемой двумя различными метрическими формами. Независимо от Кристоффеля аналогичную задачу решил Рудольф Липшиц, чья статья появилась годом позже[1].
Элементарное понятие о символах Кристоффеля
Введение
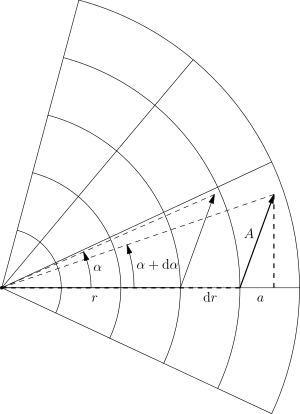
Наглядное представление о символах Кристоффеля можно получить на примере полярной системы координат. В этой системе координатами точки являются расстояние от неё до полюса и угол направления от полярной оси.
Координатами вектора, как и в прямоугольной системе координат, следует считать дифференциалы (бесконечно малые приращения) этих величин: .
Пусть есть вектор с компонентами , где имеет геометрический смысл проекции вектора на радиальный луч (проходящий через начало вектора), а — угол, под которым вектор виден из полюса. В прямоугольной системе координат компоненты вектора не меняются при параллельном переносе. В полярной системе координат это не так (см. рис 1 и 2).
Символы Кристоффеля как раз и выражают изменение компонент вектора при его параллельном переносе.
Параллельный перенос вдоль координатных линий
При смещении вектора вдоль радиального луча на расстояние , его компонента , очевидно, не меняется, но вторая его координата () уменьшается (рис. 1). Величина вектора остаётся неизменной, поэтому . Отсюда получается (пренебрежением величинами второго и большего порядков малости):
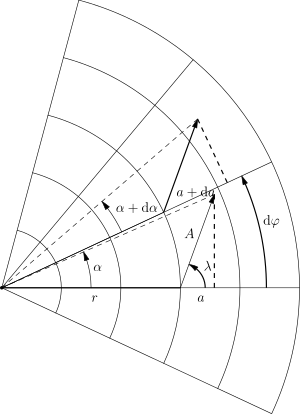
При параллельном переносе вдоль дуги меняются обе координаты и (рис. 2). Очевидно, , , и поэтому:
Кроме этого, так как , , и , то
Параллельный перенос в произвольном направлении
При произвольном малом смещении вектора (когда меняются и , и ) изменения компонент надо складывать:
Полученные выражения имеют общую структуру: изменение компонент вектора пропорционально всем компонентам вектора и пропорционально величине сдвига вектора. Коэффициенты пропорциональности (без общего минуса) и называются символами Кристоффеля.
В более общих обозначениях , , и можно записать (имея в виду сумму по повторяющимся индексам):
Здесь символы Кристоффеля , , а все остальные равны нулю.
В прямоугольной системе координат все символы Кристоффеля равны нулю, так как компоненты вектора не изменяются при параллельном переносе. Из этого можно сделать вывод, что символы Кристоффеля не образуют тензор: если тензор равен нулю в какой-либо системе координат, то он равен нулю во всех остальных системах координат.
Символы Кристоффеля первого и второго рода
Символы Кристоффеля второго рода можно определить как коэффициенты разложения ковариантной производной координатных векторов по базису:
Символы Кристоффеля первого рода :
Выражение через метрический тензор
Символы Кристоффеля связности Леви-Чивиты для карты могут быть определены из отсутствия кручения, то есть,
и того условия, что ковариантная производная метрического тензора равна нулю:
Для сокращения записи символ набла и символы частных производных часто опускаются, вместо них перед индексом, по которому производится дифференцирование, ставится точка с запятой «;» в случае ковариантной и запятая «,» в случае частной производной. Таким образом, выражение выше можно также записать как
Явные выражения для символов Кристоффеля второго рода получаются, если сложить это уравнение и другие два уравнения, которые получаются циклической перестановкой индексов:
где — контравариантное представление метрики, которое есть матрица, обратная к , находится путём решения системы линейных уравнений .
Инвариантные обозначения
Инвариантные обозначения для связности абстрагируются от конкретной системы координат и поэтому более предпочтительны при доказательстве математических теорем.
Пусть X и Y — векторные поля с компонентами и . Тогда k-я компонента ковариантной производной поля Y по отношению к X задается выражением
Условие отсутствия кручения у связности:
эквивалентно симметричности символов Кристоффеля по двум нижним индексам:
Замена координат
Несмотря на то, что символы Кристоффеля записываются в тех же обозначениях, что и компоненты тензоров, они не являются тензорами, потому что не преобразуются как тензоры при переходе в новую систему координат. В частности, выбором координат в окрестности любой точки символы Кристоффеля могут быть локально сделаны равными нулю (или обратно ненулевыми), что невозможно для тензора.
При замене переменных на базисные векторы преобразуются ковариантно:
откуда следует формула преобразования символов Кристоффеля:
Черта означает систему координат y. Таким образом, символы Кристоффеля не преобразуются как тензор. Они представляют собой более сложный геометрический объект в касательном пространстве с нелинейным законом преобразования от одной системы координат к другой.
Примечание. Можно заметить, например, из определения, что первый индекс является тензорным, то есть по нему символы Кристоффеля преобразуются как тензор.
Символы Кристоффеля в различных системах координат
Пользуясь выражением символа через метрический тензор, либо преобразованием координат, можно получить значения их в любой системе координат. В механике и физике чаще всего используются ортогональные криволинейные системы координат. В этом случае символы Кристоффеля с равными коэффициентами выражаются через коэффициенты Ламе (диагональные элементы метрического тензора) , а все остальные равны нулю.
Символы Кристоффеля первого рода выражаются так:
- при
Символы Кристоффеля второго рода:
- при
Значения для распространённых систем координат:
- В декартовой системе координат : , поэтому ковариантная производная совпадает с частной производной.
- В цилиндрической системе координат : , . Остальные равны нулю.
- В сферической системе координат : , , , , . Остальные равны нулю.
Вариации и обобщения
Разница двух аффинных связностей
является тензором. В случае если определяется в карте как связность в которой тензорные поля с постоянными компонентами параллельны, крисоффели являются компонентами полученного тензора . В этом случае отсутствие кручения у обеих связностей влечёт симметрию тензора
- .
Можно выбрать другую базовую связность . Например, объявив параллельным произвольное поле ортонормированных реперов; так это делается в методе подвижного репера. Поскольку в этом случае связность может иметь ненулевое кручение, то вообще говоря . Однако поскольку обе связности римановы, выполняется другое, не менее полезное соотношение:
- .
Иначе говоря является 1-формой на многообразии со значениями в антисимметрических операторах на касательном пространстве.
См. также
Примечания
- Математика XIX века. Том II: Геометрия. Теория аналитических функций / Под ред. Колмогорова А. Н., Юшкевича А. П.. — М.: Наука, 1981. — С. 89. — 270 с.
Литература
- Димитриенко Ю. И. Тензорное исчисление. — М.: Высшая школа, 2001. — 575 с. — ISBN 5-06-004155-7.
- Победря Б. Е. Лекции по тензорному анализу. — М.: Издательство Московского университета, 1974. — 206 с.
