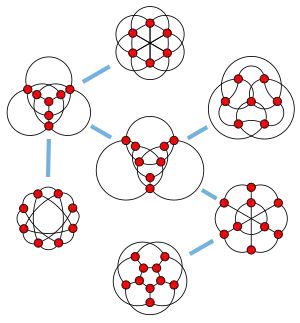
Незацепленное вложение графа

Две зацепленные кривые, образующие зацепление Хопфа.

Говорят, что две непересекающиеся кривые в евклидовом пространстве не зацеплены, если существует непрерывное движение кривых, которое преобразует их в две незацепленные копланарные окружности без прохождения одной кривой через другую или через себя. Если такого непрерывного движения нет, говорят, что кривые зацеплены. Зацепление Хопфа, образованное двумя окружностями, которые проходят через диск, натянутый на эти окружности, даёт простейший пример пары зацепленных кривых, но кривые могут быть зацеплены существенно более сложным образом. Если кривые не зацеплены, можно найти (топологический) диск в пространстве, ограниченный первой кривой и не пересекающийся со второй. И обратно, если такой диск существует, кривые не зацеплены.

Коэффициент зацепления двух замкнутых кривых в трёхмерном пространстве является топологическим инвариантом кривой — это число, определённое для кривых одним из эквивалентных способов, которое не меняется, если двигать кривые в пространстве непрерывно без пересечения друг друга или себя. Коэффициент зацепления находится путём проектирования вложения на плоскость и подсчёта определённым образом числа проходов первой кривой над второй (со знаком +1 или −1 в зависимости от направления прохода). Проекция должна быть «правильной», что означает, что никакие две вершины не проецируются в одну точку, никакая вершина не проецируется внутрь ребра и в любой точке проекции, где рёбра пересекаются, они пересекаются трансверсально. При таких ограничениях любая проекция ведёт к одному и тому же коэффициенту зацепления. Коэффициент зацепления незацепленных кривых равен нулю, а поэтому, если пара кривых имеет ненулевой коэффициент зацепления, две кривые должны быть зацеплены. Однако существуют примеры зацепленных кривых, имеющих нулевой коэффициент зацепления, например, зацепление Уайтхеда.

Вложение графа в трёхмерное пространство состоит из отображения вершин графа в точки пространства и отображений рёбер в кривые, так что каждая конечная точка ребра отображается в конечную точку соответствующей кривой и кривые, соответствующие двум различным рёбрам, не пересекаются (разве что в общих конечных точках). Любой конечный граф имеет конечное (возможно экспоненциальное) число различных простых циклов, и, если граф вложен в трёхмерное пространство, каждый такой цикл образует простую замкнутую кривую. Можно вычислить коэффициент зацепления каждой непересекающейся пары кривых, образованных таким образом. Если все пары циклов имеют нулевой коэффициент зацепления, говорят, что вложение является незацепленным[6][1][2].

В некоторых случаях граф может быть вложен в пространство таким образом, что для каждого цикла в графе можно найти диск, ограниченный этим циклом, который не пересекает другие элементы графа. В этом случае цикл должен быть не зацеплен с другими циклами графа, не пересекающими его. Говорят, что вложение плоское, если любой цикл ограничивает диск описанным образом[2]. Аналогично определение "хорошего вложения " приведено в статье Мотвани, Рагунатана и Сарана Motwani, Raghunathan, Saran, 1988. См. также Saran (1989) и Böhme (1990).</ref>. Плоское вложение обязательно является незацепленным, но могут существовать незацепленные вложения, не являющиеся плоскими. Например, если G является графом, образованным двумя раздельными циклами, и при вложении получается зацепление Уайтхэда, вложение является незацепленным, но не плоским.

Говорят, что граф существенно зацеплен, если при любом вложении получается всегда зацепленное вложение. Хотя незацепленное и плоское вложения не то же самое, графы, имеющие незацепленные вложения оказываются теми же графами, что и графы, имеющие плоские вложения[7].

Петерсеново семейство графов.

Как показал Сакс[1], все семь графов петерсенова семейства существенно зацеплены, и не имеет значения, как эти графы вложены в пространство, при любом вложении они имеют два зацепленных цикла. Эти графы включают полный граф ${\displaystyle K_{6}}$, граф Петерсена, граф, образованный удалением ребра из полного двудольного графа ${\displaystyle K_{4,4}}$, и полный трёхдольный граф ${\displaystyle K_{3,3,1}}$.

Любой планарный граф имеет плоское и незацепленное вложение — просто вкладываем граф в плоскость, находящуюся в (трёхмерном) пространстве. Если граф планарен, это единственный путь вложения графа плоско и незацепленно — любое плоское вложение можно непрерывно деформировать во вложение на плоскости. И наоборот, любой непланарный незацепленный граф имеет множественные незацепленные вложения[2].

Верхушечный граф. Если планарная часть графа вложена в плоскость, находящуюся в пространство, верхушка графа (нарушающая планарность вершина) помещается над плоскостью и соединяется прямыми отрезками, и получаемое вложение является плоским.

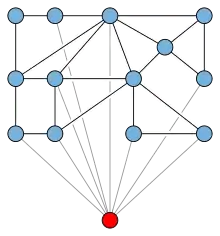
Верхушечный граф, образованный добавлением одной вершины к планарному графу, также имеет плоское и нецеплённое вложение — вкладываем планарную часть графа на плоскость, помещаем верхушку графа (нарушающую планарность вершину) над плоскостью, а затем проводим рёбра из верхушки в смежные ей вершины в виде отрезков. Любая замкнутая кривая на плоскости ограничивает диск, который не проходит через другой элемент графа, а любая замкнутая кривая через верхушку ограничивает диск над плоскостью, который не проходит через любой другой элемент графа[2].

Если граф имеет незацепленное или плоское вложение, то модификация графа путём разделения или объединения его рёбер, добавления или удаления кратных рёбер между парой вершин или проведения Y-Δ-преобразований, при котором вершина степени три заменяется треугольником, соединяющим три соседа, или обратно, приводит к сохранению существования плоского или незацепленного вложения[2]. В частности, в кубическом планарном графе (в котором все вершины имеют в точности три соседа, как у куба) можно сделать копии любого независимого множества вершин путём осуществления Y-Δ-преобразования, добавления кратных копий рёбер в полученных треугольниках, а затем осуществления обратного Δ-Y-преобразования.

Если граф ${\displaystyle G}$ имеет незацеплённое или плоское вложение, то любой минор графа ${\displaystyle G}$ (граф, образованный стягиванием рёбер и удалением рёбер и вершин) также имеет незацепленное или плоское вложение. Удаление не может разрушить возможность незацепленного или плоского вложения, а стягивание можно осуществить, оставив одну конечную точку стягиваемого ребра на месте и переключив все рёбра, инцидентные противоположной вершине. Таким образом, по теореме Робертсона — Сеймура, имеющие незацепленное вложение графы имеют характеризацию запрещёнными графами как графы, не содержащие любого из конечного набора миноров[3].

Множество запрещённых миноров для допускающих незацепленное вложение графов было выявлено Саксом[1] — семь графов петерсенова семейства являются минорно минимальными существенно зацепленными графами. Однако Сакс не смог доказать, что только эти графы являются минорно минимальными зацеплёнными графами, и это сделали Робертсон, Сеймур и Томас[4].

Характеризация запрещёнными минорами допускающих незацепленное вложение графов ведёт к алгоритму с полиномиальным временем работы их распознавания, но при этом этот алгоритм не строит действительное вложение. Каравабайши, Крейцер и Мохар[5] описали алгоритм с линейным временем работы, проверяющий, вложим ли граф незацепленно, и, если вложим, строит плоское вложение графа. Их алгоритм находит большие планарные подграфы внутри заданного графа, такие, что, если существует незацепленное вложение, они представляют планарное вложение подграфа. Повторно упрощая граф, когда такой подграф находится, они сводят задачу к задаче, в которой оставшийся граф ограничен древесной шириной, и с этого момента задача может быть решена с помощью динамического программирования.

Задача эффективной проверки, является ли заданное вложение плоским или незацепленным, была поставлена Робертсоном, Сеймуром и Томасом[2]. Задача остаётся нерешённой и по сложности эквивалентна задаче распутывания узла, задаче проверки, является ли кривая в пространстве незаузлённой[5]. Известно, что проверка незаузлённости (а следовательно, и незацепленного вложения) принадлежит классу NP, но неизвестно, принадлежит ли она классу NP-полных задач[8].

Инвариант Колен де Вердьера — это число, определённое для любого графа на основе алгебраической теории графов. Граф с инвариантом Колен де Вердьера, не превосходящим μ, для любой фиксированной постоянной μ образует замкнутое по минорам семейство, и несколько первых таких семейств хорошо известны — графы с μ ≤ 1 представляют собой линейные леса (несвязное объединение путей), графы с μ ≤ 2 представляют собой внешнепланарные графы, а графы с μ ≤ 3 представляют собой планарные графы. Как предположили Робертсон, Сеймур и Томас[2] и доказали Ловаш и Схрейвер[9], графами с μ ≤ 4 в точности являются графы с незацепленным вложением.

Незацепленный вершинный граф, несократимый преобразованием YΔY.

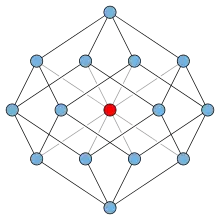
Планарные графы и вершинные графы допускают незацепленное вложение, как и графы, получаемые Y-Δ преобразованиями из них[2]. YΔY сократимые графы — это графы, которые могут быть сведены к одной вершине преобразованием Y-Δ, удалением изолированных вершин и висячих вершин (вершин степени 1) и заменой дуг при вершине со степенью два одной дугой. Эти графы также замкнуты по минорам. Однако существуют незацепленные YΔY-несократимые графы, такие как вершинный граф, образованный соединением верхушки (вершины, нарушающей планарность) со всеми вершинами степени три ромбододекаэдра[10]. Существуют также незацепленные графы, которые не могут быть преобразованы с помощью Y-Δ-преобразований, удалением изолированных и висячих вершин и заменой дуг при вершине со степенью два одной дугой в вершинный граф. Например, корона с десятью вершинами имеет незацепленное вложение, но не может быть преобразована в вершинный граф указанным выше образом[2].

Связанным с понятием незацепленного вложения является понятие незаузлённого вложения. Это такое вложение графа, что никакой простой цикл не образует нетривиальный узел. В графы, не имеющие незаузлённого вложения, входят K₇ и K_3,3,1,1[6][11]. Однако существуют минимальные запрещённые миноры для незаузлённых вложений, которые не образованы (в отличие от указанных двух графов) добавлением одной вершины к существенно зацепленному графу[12].

Можно определить семейства графов по присутствию или отсутствию более сложных узлов и зацеплений в их вложении[3][13], или по незацепленному вложению в трёхмерное многообразие, отличному от евклидова пространства[14]. Флапан, Наими и Поммершейм[15] определили вложение графа как трижды зацепленное, если существуют три цикла, ни один из которых не может быть отделен от двух других. Они показали, что K₉ не трижды существенно зацеплены, а K₁₀ зацеплен[16]. Более обще, можно определить n-зацепленное вложение для любого ${\displaystyle n}$ как вложение, содержащее ${\displaystyle n}$-компонентное зацепление, которое не может быть разделено топологической сферой на две раздельные части. Минорно минимальные существенно ${\displaystyle n}$-зацепленные графы известны для всех ${\displaystyle n}$[17].

Вопрос, имеет ли ${\displaystyle K_{6}}$ зацепленное или плоское вложение, поставил в топологическом исследовательском сообществе в начале 1970 Боте[18]. К незацепленному вложению привлёк внимание теоретиков графов Сакс[1], который предложил несколько связанных задач, включая задачу поиска характеризации запрещёнными графами графов с незацепленным или плоским вложением. Сакс показал, что семь графов петерсенова семейства (включая ${\displaystyle K_{6}}$) не имеют таких вложений. Как заметили Нешетрил и Томас[3], допускающие незацепленное вложение графы замкнуты по минорам графа, откуда следует по теореме Робертсона — Сеймура, что характеризация запрещёнными графами существует. Доказательство существования конечного числа препятствующих графов не ведёт к явному описанию этого множества запрещённых миноров, но из результатов Сакса следует, что семь графов петерсенова семейства принадлежат множеству. Эти задачи были окончательно решены Робертсоном, Сеймуром и Томасом[4][7], которые показали, что эти семь графов петерсенова семейства являются единственными минимальными запрещёнными минорами для таких графов. Таким образом, незацепленно вложимые графы и плоско вложимые графы являются одним и тем же множеством графов и оба семейства можно определить как графы, не содержащие элементы семейства петерсена в качестве миноров.

Сакс[1] также задал вопрос о границах числа рёбер и хроматического числа вложимых без зацепления графов. Число рёбер во вложимом без зацепления графе с ${\displaystyle n}$ вершинами не превосходит ${\displaystyle 4n-10}$ — максимальные вершинные графы с ${\displaystyle n>4}$ имеют в точности такое число рёбер[1], а Мадер[19] доказал верность верхней границы для более общего класса свободных от K₆ миноров графов. В 1985 году показано, что вопрос Сакса о хроматическом числе был бы решён, если была бы доказана гипотеза Хадвигера, что любой ${\displaystyle k}$-хроматический граф имеет в качестве минора полный граф с ${\displaystyle k}$ вершинами[3]. Доказательство Робертсона, Сеймура и Томаса[20] случая ${\displaystyle k=6}$ гипотезы Хадвигера достаточен для решения вопроса Сакса — графы без зацеплений можно раскрасить максимум пятью цветами, поскольку любой 6-хроматический граф содержит минор ${\displaystyle K_{6}}$ и не является незацепленным, и существуют незацепленные графы, такие как ${\displaystyle K_{5}}$, требующие пять цветов. Из теоремы о снарках следует, что любой кубический вложимый без зацепления граф является рёберно раскрашиваемым в 3 цвета.

Изучение вложений без зацеплений началось при исследовании алгоритмов в конце 1980-х годов[21][22]. Алгоритмически задача распознавания вложимых без зацеплений и плоско вложимых графов была решена, когда была доказана характеризация запрещёнными минорами — алгоритм Робертсона и Сеймура[23] может быть использован для проверки за полиномиальное время, содержит ли заданный граф любой из семи запрещённых миноров[24]. Этот метод не строит незацепленное или плоское вложение, если оно существует, но алгоритм, строящий вложение[25], а позднее найден более эффективный алгоритм, работающий за линейное время[5].

На последний вопрос Сакса[1] о возможности аналогии теоремы Фари для незацепленных графов ответа пока нет. Вопрос ставится следующим образом: когда существование незацепленного или плоского вложения с кривыми или кусочно-линейными рёбрами влечёт существование незацепленного или плоского вложения, в котором рёбра являются отрезками?